机器学习入门例子--预测浏览量
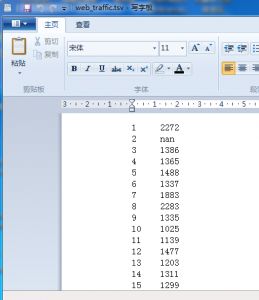
首先，我们要做的是把这些数据读到我们的程序里去。方法是使用SciPy的genfromtxt()，首先打开开始菜单中的所有应用程序找到Python 2.7,选择第一个IDLE(Python GUI)或者打开cmd，然后再敲入python，也是可以的:
然后输入：
import scipy as sp
data=sp.genfromtxt(“web_traffic.tsv”,delimiter=”\t”)
前者表示路径名，要注意在自己电脑上设置成相应的路径名，然后第二个参数是分隔符，由于原文件中使用的制表符隔开数据的，所以这里是\t。为了查看以下是否已经成功将数据读取到相应变量中，我们可以用如下的方法检验：
其中观察到第二行数据的第二列nan，它表示无效数据。然后，我们再敲入：
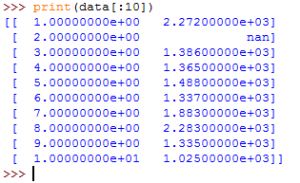
>>>print(data.shape),显式如下：
我们需要把数据分成两个向量也许更好。它们分别是向量x和向量y。使得它们可以对应监督学习中的输入和输出。第一个向量x表示第一列时间，向量y表示第二列点击量。操作如下：
刚才提到了无效数据，首先看看有多少个无效数据，也就是有多少行含有“nan”。敲入：
看来不多，只有8行。我们能够手动删除它们？那如果很多无效数据了呢，所以我们还是借助SciPy的强大功能吧。敲入：
学过程序的人应该都能看得明白，~表示取反，这里就表示取有效的数据，当然具体细节我们暂时不需要明白，只要知道它的功能即可。好的，现在来检测一下是不是已经剔除了无效数据呢？
发现原来的2被我们剔除了，再来看下y吧：
原来那个nan没了。好的，数据处理好了，接下来想可视化以下，我们把它展示在一张图中，这就要借助工具Matplotlib.把下图中的>>>后面的命令敲入：
下面两幅图是一样的
plt.gird()
plt.show()
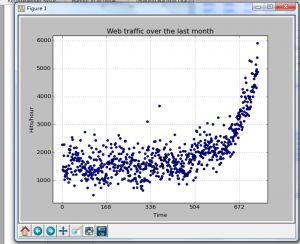
可以看到图：
这个就是之前的数据绘成的图，x，y轴分别表示时间和点击量。数据到这里基本就处理好了。下面应该是机器学习算法部分了。我们要选择一个算法去预测将来的点击量，这是明显的监督学习。上图给出的数据便是训练样本。在建立我们第一个模型之前我们需要先设计一个评估函数，用来判断什么样的模型才是好的。也就是误差函数，可以这样来计算，用模型的预测值-真实值（训练样本已经提供）的差的平方来评估(为什么它能评估，也是很好理解的)。即：
def error(f,x,y):
return sp.sum((f(x)-y)**2)
容易知道，这其实是一个拟合问题，把这些数据拟合到最佳模型（即一个函数，再用这个函数去预测新数据）。从最简单的情况开始，我们首先去一条直线去拟合这些数据。SciPy提供了函数polyfit()，只要给定数据x和y以及多项式的阶数（直线是1次函数），它就能找到模型的函数，使得之前定义的误差函数达到最小（只有误差最小才表面模型最好额）。敲入：fp1,residuals,rank,sv,rcond=sp.polyfit(x,y,1,full=True)
fp1,residuals,rank,sv,rcond=sp.polyfit(x,y,1,full=True)
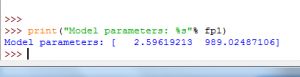
函数polyfit()返回拟合模型函数的参数fp1，并且通过把full设置成True,我们还能获得其他的相关信息，在这里只有residuals是我们感兴趣的，它是真的误差。打印参数：
print("Model parameters：%s"% fp1)
打印误差：print(residuals)
这意味着：f(x)=2.59619213 * x +989.02487106
然后我们用函数poly1d()来创建模型函数：
f1=sp.poly1d(fp1)
注意这里是数字1不是字母l，不然就看到它报错了。现在我们用f1()去拟合数据，让我们看看拟合的效果：（由于画图需要之前的代码，所以写成一个脚本）：
import sys
import scipy as sp
data=sp.genfromtxt("E:\python\data\ch01\data\web_traffic.tsv",delimiter="\t")
print(data[:10])
x=data[:,0]
y=data[:,1]
sp.sum(sp.isnan(y))
x=x[~sp.isnan(y)]
y=y[~sp.isnan(y)]
import matplotlib.pyplot as plt
plt.scatter(x,y)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*7*24 for w in range(10)],
['week %i'%w for w in range(10)])
plt.autoscale(tight=True)
plt.grid()
fp1,residuals,rank,sv,rcond=sp.polyfit(x,y,1,full=True)
f1=sp.poly1d(fp1)
fx=sp.linspace(0,x[-1],1000)
plt.plot(fx,f1(fx),linewidth=4)
plt.legend(["d=%i" %f1.order],loc="upper left")
plt.show()
input()
拟合效果显然不好，因为是一阶的直线。这个方法是可以用来学习机器学习各种算法的，而scikit-learn是提供了各种机器学习算法包，可供你直接调用。暂时就不介绍了，今天只写这么多。