拉格朗日乘子法与KKT条件解决优化问题

SVM支持向量机是目前非常好用的一种分类算法，但是其中的原理推导涉及了一些数学知识：例如其中在处理我们构建得到的数学模型时，最优化问题中就使用到了拉格朗日乘子法与KKT条件。

通常需要解决的优化问题有三类：

1.无约束的优化问题

   min f(x)                         

求取f(x)的导数使其为零，求解出候选值，在其中验证选择出最优值，就是高中常用的方法。

2.有等式约束的优化问题

   min f(x)

   s.t. h_i(x)=0                 

使用拉格朗日乘子法，构建函数L(a,x)=f(x)-a*h_i(x),a是>=0的拉格朗日乘子，令L(a,x)对各变量求导使其为零，获得候选值的集合，这个方法在高数中也曾用过。

3.有不等式约束的优化问题

   min f(x)                        

   s.t. g_i(x)>=0               

         h_i(x)=0                   

对此同样把目标函数、等式不等式约束写为一个式子：L(a,b,x)=f(x)-a*g_i(x)-b*h_i(x)，KKT条件就是说找到最优值一定满足这三个条件：①L（a,b,x)对x求导为零 ②h(x)=0 ③a*g(x)=0，求取这三个等式得到最优候选值。

但是需要注意使用拉格朗日乘子法与KKT是有前提条件的：即目标函数f(x)必须是凸函数。

 

拉格朗日乘子法

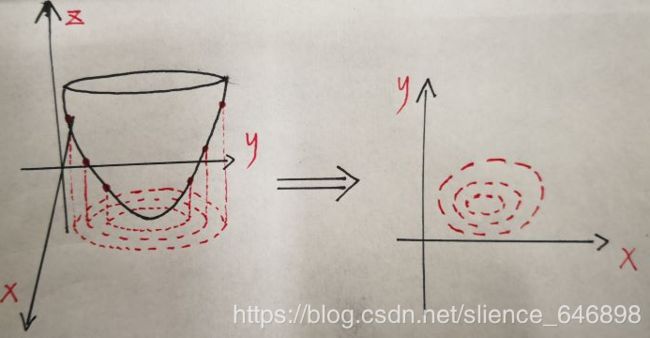
原理：设想目标函数z=f(x)，x是向量，z与其对应有不同的值，可以把z投影到x构成的平面（或曲面）上，做出类似等高线的图像。

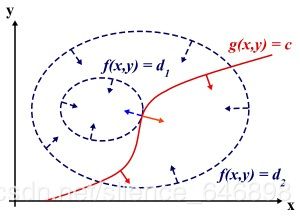
那么在这个平面（曲面）上，它的约束等式h(x)=0也可以在上面做出

明显可知h(x)=0与f(x)等高线的交点就是既满足在可行解域中（在f(x)上），也满足它的等式约束条件（在h(x)上）。但是可知交点的解肯定不是最优解，因为是一个交点，那么它意味着h(x)肯定还会穿过外边其它的等高线获得值更大（或更小）的交点！

故因此仅当约束函数与f(x)的等高线相切时，才有可能获得最优值。两者相切则在切点处两个函数的法向量方向相同，即f(x)的梯度等于a*h(x)的梯度，而这正是上面所说的"构建拉格朗日函数L(a,x)=f(x)-a*h(x)，使其对参数求导并等于零"。

通过这些也就可以理解了为什么拉格朗日乘子法和KKT条件要求目标函数f(x)必须是凸函数了，因为只有是凸函数，它的投影出的等高线才是规律的：即等高线自内向外一定是逐渐增大（或减小）的！如果是非凸函数，那么它投影出来的等高线变化一定是不规律的！如果等高线变化是不规律的，那么就无法确定说明在切点处就会取得最优值！

 

KKT条件

KKT条件是满足强对偶条件的优化问题的必要条件。

同样将目标函数、等式不等式约束条件写为同一个式子，也称为拉格朗日函数：L（a,b,x)=f(x)-a*g(x)-b*h(x)，a是>=0的拉格朗日乘子。如果目标求min f(x)

那么f(x)可以写为 max L(a,b,x):因为约束条件h(x)=0(条件①)，a*g(x)>=0，为了使L(a,b,x)最大则需要令a*g(x)=0(条件②），故L(a,b,x)才能取得最大为f(x)。

目标则变成求 min max L(a,b,x)，由于我们的优化是满足强对偶的（强对偶就是说对偶式子的最优值是等价于原问题的最优值的），使用对偶表达式：min max L(a,b,x)=max min L(a,b,x)

令L(a,b,x)在某处x0取得最小值，则变为 max f(x0)-a*g(x0)-b*h(x0)!L(a,b,x)要取得最小值则应令其导数应等于零（条件③）

那么上面的三个条件就是KKT条件，KKT条件也可以看成为是拉格朗日乘子法的泛化。

 

学习自：https://blog.csdn.net/xianlingmao/article/details/7919597

              https://blog.csdn.net/c406495762/article/details/78072313