机器学习之&&SVM支持向量机入门:Maximum Margin Classifier

概率论只不过是把常识用数学公式表达了出来。

——拉普拉斯

0. 前言

这是一篇SVM的入门笔记，来自我对PlusKid、JerryLead、July等大神文章的拜读心得，说是心得还不如说是读文笔记，希望在自己理解的层面上给予SVM这个伟大的机器学习算法概要介绍，让更多的热爱机器学习的伙伴们进入到SVM的世界。PS：文章会以问答的形式为主要结构。

1.概念

1.1.什么是SVM？

支持向量机即 Support Vector Machine，简称 SVM 。（第一次接触SVM是在阿里大数据竞赛的时候，大家都在讨论用什么样的方法去挣阿里那100W的奖金(鄙人因为能力有限进入决赛阶段，但是因为模型优化问题，名落松山)，SVM、LR、协同过滤等等）SVM是Vapnik和Cortes于1995年首先提出的，它旨在解决小样本、非线性、高纬(因为现实应用中的数据多为这般特性)等特性的数据特征的模式识别问题，特别在分类问题中，一直被大家认为是一种现有的可用的效果最好的分类算法之一。(甚至很多人觉得之一可以去掉，但是神经网络"大大"不愿意-。-)

1.2.为什么会有SVM？

前面已经说过了SVM在解决小样本、非线性、高纬数据上的优势，那么我们就从线性分类器开始逐步探讨为什么会有SVM的出现？

1.2.1.线性分类器

给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点，用y表示类别（y可以取1或者-1，分别代表两个不同的类,有些地方会选 0 和 1 ，当然其实分类问题选什么都无所谓，只要是两个不同的数字即可，不过这里选择 +1 和 -1 是为了方便 SVM 的推导，后面就会明了了），一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane），这个超平面的方程可以表示为（ wT中的T代表转置）：

(为什么会有这个形式化表示的超平面方程，请猛戳这里)

一个超平面，在二维空间中的例子就是一条直线。我们希望的是，通过这个超平面可以把两类数据分隔开来，比如，在超平面一边的数据点所对应的  y  全是 -1 ，而在另一边全是 1 。具体来说，我们令  f(x)=wTx+b  ，显然，如果  f(x)=0  ，那么  x  是位于超平面上的点。我们不妨要求对于所有满足  f(x)<0  的点，其对应的  y  等于 -1 ，而  f(x)>0  则对应  y=1  的数据点。当然，有些时候（或者说大部分时候）数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在，不过关于如何处理这样的问题我们后面会讲(SVM核函数的出现)，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。

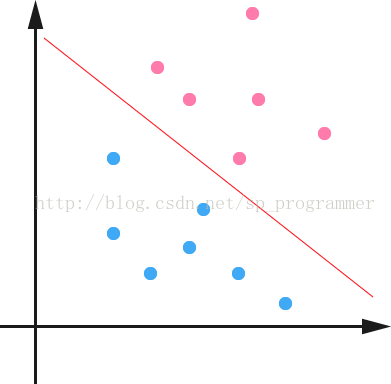
如下图所示，两种颜色的点分别代表两个类别，红颜色的线表示一个可行的超平面。在进行分类的时候，我们将数据点  x 代入  f(x)  中，如果得到的结果小于 0 ，则赋予其类别 -1 ，如果大于 0 则赋予类别 1 。如果  f(x)=0 ，则很难办了，分到哪一类都不是。事实上，对于  f(x)  的绝对值很小的情况，我们都很难处理，因为细微的变动（比如超平面稍微转一个小角度）就有可能导致结果类别的改变。理想情况下，我们希望  f(x)  的值都是很大的正数或者很小的负数，这样我们就能更加确信它是属于其中某一类别的。

当然，有些时候，或者说大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在(不过关于如何处理这样的问题我们后面会讲)，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。

    换言之，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1。

    接下来的问题是，如何确定这个超平面呢？从直观上而言，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以，得寻找有着最大间隔的超平面。

2.SVM之函数间隔(functional margin)与几何间隔(geometrical margin)

2.1.什么是函数间隔和几何间隔及其关系？

为了让欲分类的点远离超平面(这样分类效果更好)，我们可以用(y*(w*x+b))的正负性来判定或表示分类的正确性，因此我们定义函数间隔如下：

注意前面乘上类别  y  之后可以保证这个 margin 的非负性（因为  f(x)<0  对应于  y=−1  的那些点），而点到超平面的距离定义为 geometrical margin 。不妨来看看二者之间的关系。

如图所示，对于一个点  x  ，令其垂直投影到超平面上的对应的为  x0  ，由于  w  是垂直于超平面的一个向量，我们有

x=x0+γw∥w∥

又由于  x0  是超平面上的点，满足  f(x0)=0  ，代入超平面的方程即可算出

γ=wTx+b∥w∥=f(x)∥w∥

不过，这里的  γ  是带符号的，我们需要的只是它的绝对值，因此类似地，也乘上对应的类别  y 即可，因此实际上我们定义 geometrical margin 为：

γ˜=yγ=γˆ∥w∥

显然，functional margin 和 geometrical margin 相差一个  ∥w∥  的缩放因子。按照我们前面的分析，对一个数据点进行分类，当它的 margin 越大的时候，分类的确信度越大。对于一个包含  n  个点的数据集，我们可以很自然地定义它的 margin 为所有这  n  个点的 margin 值中最小的那个。于是，为了使得分类的 confidence 高，我们希望所选择的 hyper plane 能够最大化这个 margin 值。

2.2.最大间隔分类原理，及其数学表示。

这里我们有两个 margin 可以选，不过 functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放  w  的长度和  b  的值，这样可以使得  f(x)=wTx+b  的值任意大，亦即 functional margin  γˆ  可以在 hyper plane 保持不变的情况下被取得任意大，而 geometrical margin 则没有这个问题，因为除上了  ∥w∥  这个分母，所以缩放  w  和  b  的时候  γ˜  的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。这样一来，我们的 maximum margin classifier 的目标函数即定义为

maxγ˜

同时需满足一些条件，根据间隔的定义，有

yi(wTxi+b)=γˆi≥γˆ,i=1,…,n

其中  γˆ=γ˜∥w∥  ，根据我们刚才的讨论，即使在超平面固定的情况下， γˆ  的值也可以随着  ∥w∥  的变化而变化。由于我们的目标就是要确定超平面，因此可以把这个无关的变量固定下来，固定的方式有两种：一是固定  ∥w∥  ，当我们找到最优的  γ˜  时  γˆ  也就可以随之而固定；二是反过来固定  γˆ  ，此时  ∥w∥  也可以根据最优的  γ˜  得到。处于方便推导和优化的目的，我们选择第二种，令  γˆ=1  ，则我们的目标函数化为：

max1∥w∥,s.t.,yi(wTxi+b)≥1,i=1,…,n

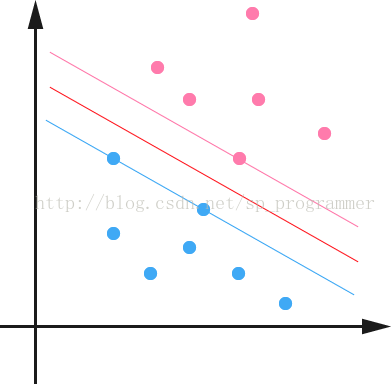
通过求解这个问题，我们就可以找到一个 margin 最大的 classifier ，如下图所示，中间的红色线条是 Optimal Hyper Plane ，另外两条线到红线的距离都是等于 γ ˜  的：

以上就是SVM的基本原理，总结下来就是一句话求一个最大分类间隔的超平面，让数据分类效果很理想。但是为什么叫支持向量机？难道SVM就这么简单？一切还得在下篇博客见分晓。