C++实现复数矩阵求逆 matlab inv
C++实现复数矩阵求逆 matlab inv
- 一、引言
- 二、原理
- 2.1 实数矩阵求逆
- 2.2 复数矩阵求逆
- 三、代码
- 四、测试
一、引言
之前偶尔一次有用到将matlab转为C++语言的需求,其中matlab有一个inv函数可以非常方便的求矩阵的逆,甚至是复数矩阵。而C++中没有类似的函数。在csdn上有一个matlab2c的库的博客(github地址第80行开始),但是只有实数矩阵求逆的代码,而我又在百度上搜到一篇文献中写到将复数矩阵转为两个实数矩阵然后在进行求解。然后我就将两个代码一结合,就实现了复数矩阵求逆。经验证与matlab的inv函数结果一致。
二、原理
2.1 实数矩阵求逆
这里直接给出matlab2c中求实数矩阵的代码,其中函数inv的两个参数:a代表实数矩阵,用double二维数组存储、num代表这个矩阵的行数/列数。
void swap(double* a, double* b); //声明子程序
double** inv(double** a, int num)
{
int* is, * js, i, j, k;
int n = num;
double temp, fmax;
double** tp = new double* [num];
for (int i = 0; i < num; i++) tp[i] = new double[num];
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
tp[i][j] = a[i][j];
}
}
is = new int[n];
js = new int[n];
for (k = 0; k < n; k++)
{
fmax = 0.0;
for (i = k; i < n; i++) {
for (j = k; j < n; j++)
{
temp = fabs(tp[i][j]);//找最大值
if (temp > fmax)
{
fmax = temp;
is[k] = i; js[k] = j;
}
}
}
if ((fmax + 1.0) == 1.0)
{
delete[] is;
delete[] js;
return NULL;
}
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[k][j], &tp[i][j]);//交换指针
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[i][k], &tp[i][j]); //交换指针
tp[k][k] = 1.0 / tp[k][k];
for (j = 0; j < n; j++)
if (j != k)
tp[k][j] *= tp[k][k];
for (i = 0; i < n; i++)
if (i != k)
for (j = 0; j < n; j++)
if (j != k)
tp[i][j] = tp[i][j] - tp[i][k] * tp[k][j];
for (i = 0; i < n; i++)
if (i != k)
tp[i][k] *= -tp[k][k];
}
for (k = n - 1; k >= 0; k--)
{
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[j][i], &tp[k][i]);
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[j][i], &tp[j][k]);
}
delete[] is;
delete[] js;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
}
}
return tp;
}
void swap(double* a, double* b)
{
double c;
c = *a;
*a = *b;
*b = c;
}
2.2 复数矩阵求逆
在那篇文献中,我们可以看到将复数矩阵C拆分为实部矩阵A+虚部矩阵Bi,则
C − 1 = ( A + i B ) − 1 = ( A + B A − 1 B ) − 1 − i A − 1 B ( A + B A − 1 B ) − 1 C^{-1}=(A+iB)^{-1}=(A+BA^{-1}B)^{-1}-iA^{-1}B(A+BA^{-1}B)^{-1} C−1=(A+iB)−1=(A+BA−1B)−1−iA−1B(A+BA−1B)−1
这样就将复数矩阵求逆的过程转为求实数矩阵的逆、加、乘运算了。
代码:
complex** GetMatrixInverse(complex** src, int n) {
double** A = new double* [n];
double** B = new double* [n];
for (int i = 0; i < n; i++) {
A[i] = new double[n];
B[i] = new double[n];
for (int j = 0; j < n; j++) {
A[i][j] = src[i][j].real();
B[i][j] = src[i][j].imag();
}
}
double** A1 = inv(A, n);
double** A1B = Mul(A1, B, n, n, n);
double** BA1B = Mul(B, A1B, n, n, n);
double** AjBA1B = Add(A, BA1B, n, n);
double** AjBA1B_1 = inv(AjBA1B, n);
double** A1B_AjBA1B_1 = Mul(A1B, AjBA1B_1, n, n, n);
complex** res = new complex * [n];
for (int i = 0; i < n; i++) {
res[i] = new complex[n];
for (int j = 0; j < n; j++) {
res[i][j].real(AjBA1B_1[i][j]);
res[i][j].imag(-1.0 * A1B_AjBA1B_1[i][j]);
}
}
return res;
}
三、代码
完整代码如下:(包含main函数中测试代码)
#include
using namespace std;
// 矩阵加法 a+b,其中a、b均为n*m型矩阵
double** Add(double** a, double** b, int n, int m) {
double** res = new double* [n];
for (int i = 0; i < n; i++) res[i] = new double[m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
res[i][j] = a[i][j] + b[i][j];
}
}
return res;
}
// 矩阵乘法,a*b,a为n*m型矩阵,b为m*o型矩阵
double** Mul(double** a, double** b, int n, int m, int o) {
double** res = new double* [n];
double temp = 0.0;
for (int i = 0; i < n; i++) res[i] = new double[o];
for (int i = 0; i < n; i++) {
for (int j = 0; j < o; j++) {
temp = 0.0;
for (int k = 0; k < m; k++) {
temp += a[i][k] * b[k][j];
}
res[i][j] = temp;
}
}
return res;
}
void swap(double* a, double* b); //声明子程序
// 实数矩阵求逆,返回a的逆,其中a为num型方阵
double** inv(double** a, int num)
{
int* is, * js, i, j, k;
int n = num;
double temp, fmax;
double** tp = new double* [num];
for (int i = 0; i < num; i++) tp[i] = new double[num];
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
tp[i][j] = a[i][j];
}
}
is = new int[n];
js = new int[n];
for (k = 0; k < n; k++)
{
fmax = 0.0;
for (i = k; i < n; i++) {
for (j = k; j < n; j++)
{
temp = fabs(tp[i][j]);//找最大值
if (temp > fmax)
{
fmax = temp;
is[k] = i; js[k] = j;
}
}
}
if ((fmax + 1.0) == 1.0)
{
delete[] is;
delete[] js;
return NULL;
}
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[k][j], &tp[i][j]);//交换指针
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[i][k], &tp[i][j]); //交换指针
tp[k][k] = 1.0 / tp[k][k];
for (j = 0; j < n; j++)
if (j != k)
tp[k][j] *= tp[k][k];
for (i = 0; i < n; i++)
if (i != k)
for (j = 0; j < n; j++)
if (j != k)
tp[i][j] = tp[i][j] - tp[i][k] * tp[k][j];
for (i = 0; i < n; i++)
if (i != k)
tp[i][k] *= -tp[k][k];
}
for (k = n - 1; k >= 0; k--)
{
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[j][i], &tp[k][i]);
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[j][i], &tp[j][k]);
}
delete[] is;
delete[] js;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
}
}
return tp;
}
void swap(double* a, double* b)
{
double c;
c = *a;
*a = *b;
*b = c;
}
complex** GetMatrixInverse(complex** src, int n) {
double** A = new double* [n];
double** B = new double* [n];
for (int i = 0; i < n; i++) {
A[i] = new double[n];
B[i] = new double[n];
for (int j = 0; j < n; j++) {
A[i][j] = src[i][j].real();
B[i][j] = src[i][j].imag();
}
}
double** A1 = inv(A, n);
double** A1B = Mul(A1, B, n, n, n);
double** BA1B = Mul(B, A1B, n, n, n);
double** AjBA1B = Add(A, BA1B, n, n);
double** AjBA1B_1 = inv(AjBA1B, n);
double** A1B_AjBA1B_1 = Mul(A1B, AjBA1B_1, n, n, n);
complex** res = new complex * [n];
for (int i = 0; i < n; i++) {
res[i] = new complex[n];
for (int j = 0; j < n; j++) {
res[i][j].real(AjBA1B_1[i][j]);
res[i][j].imag(-1.0 * A1B_AjBA1B_1[i][j]);
}
}
return res;
}
int main() {
complex** temp = new complex * [3];
for (int i = 0; i < 3; i++) {
temp[i] = new complex[3];
}
complex t1(1, 0);
temp[0][0] = t1;
temp[2][1] = t1;
temp[2][2] = t1;
complex t2(1, 1);
temp[0][2] = t2;
temp[1][1] = t2;
complex t3(0, 1);
temp[1][0] = t3;
complex t4(2, -1);
temp[0][1] = t4;
complex t5(1, 2);
temp[1][2] = t5;
complex t6(-1, 1);
temp[2][0] = t6;
cout << "原方程:" << endl;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << temp[i][j]<<" ";
}
cout << endl;
}
cout << endl <<"求逆:"<** res = GetMatrixInverse(temp, 3);
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << res[i][j] << " ";
}
cout << endl;
}
system("pause");
return 0;
}
四、测试
构造复数矩阵:
[[1, 2-i, 1+i],
[i, 1+i, 1+2i],
[-1+i, 1, 1]]
使用本代码测试结果截图:
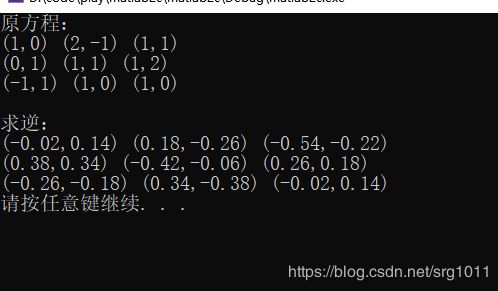
使用matlab运行结果截图:

可以看出运算结果是对的。