【总结】树状数组

概念

树状数组($BinaryIndexedTree,BIT$)也是一个区间查询和单点修改复杂度都为log(n)的数据结构。主要用于查询任意两点之间的所有元素之和。

一亿些基本操作

0.前置芝士：

1.lowbit 2.前缀和(包括二维)、差分

1.单点修改，区间查询

$BIT$的最基本操作，首先我们要知道$BIT$这东东到底是什么，先看一张烂大街的图：

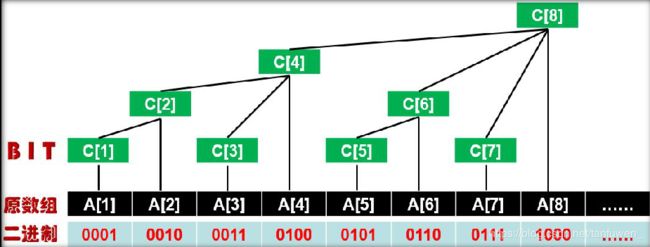
它有这样一个性质：$C[i]$一定有$lowbit(i)$个子节点(不一定是直接节点)且$C[i]=A[1]+A[2]+....A[i](前缀和)$，按照这个性质，我们就可以建出这棵树

现在我们回到正题，如何解决单点修改，区间查询？

首先是单点修改，让我们想想，假如修改$A[1]$，会对$C$中的那些节点造成影响
就是$A[1]$爬上去经过的嘛，那如何求得这些数呢，观察一下C下标，1，2，4，8，好像就是依次$\times 2$耶，是吗？看看改变A[5]的情况：

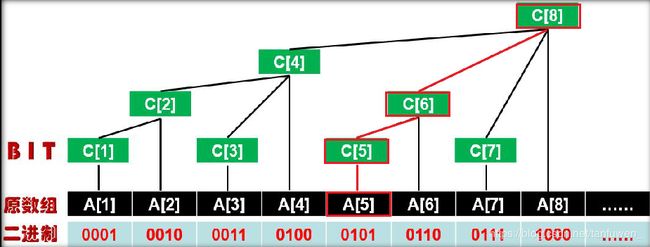
爬还是一样的爬，但下标就不一样了，5，6，8，看看规律？？？

没有？？？那看看他们的差：1，2？？？=
没看出来？？？再看看原下标对应的2进制数？？？
对了，每次增加的就是lowbit(i),其中i为下标

有了这点，单点修改就明白多了：

int lowbit(int x){//求lowbit 
	return x & -x;
}
void upd(int k,int x){//单点更新，a[k]+=x; 
	for(int i=k;i<=n;i+=lowbit(i)){
		BIT[i]+=x;
	}
}

另外，单点修改也可以用来对BIT初始化：

int t;
for(int i=1;i<=n;i++){
	scanf("%d",&t);
	upd(i,t);
}

OK，来到我们的区间查询
先说：区间查询其实是假的，它查询的其实是前缀和，但我们可以用前缀和来对出区间和
以查询前缀和[1,5] (为了简便，记A[1]+A[2]+…+A[n]为Sum(n))为例，为了保证查询尽量简单，我们以分割区域尽量少为标准，不难发现Sum[5]=C[4]+C[5]

又到了找规律的时候，找找5和4的关系？

额。。。有点难发现，但结合单点修改+连蒙带猜不难发现4=5-lowbit(5),那就清晰了，每次减lowbit(i)就行了，和单点修改恰恰相反

int Sum(int k,int l){
	int s=0;
	for(int i=k;i>=1;i-=lowbit(i)){
		for(int j=l;j>=1;j-=lowbit(j)){
			s+=BIT[i][j];
		}
	}
	return s;
}

2.区间修改，单点查询

前面我们已经知道树状数组可以进行单点修改，区间查询，而$BIT$的本质其实就是一个效率更快的前缀和，思考一下，前缀和的互逆运算不就是差分吗，对于查分求前缀和求到的是单点，而对查分数组进行单点修改却改的是区间($a[l]+x,a[r+1]-x$),这不就对上了吗

所以：

1. 将A的差分数组P作为原数组，建立$BIT$，
2. 区间修改：$[l,r]$中的所有数$+x$，即为$P[l]+x,P[r+1]-x$,对$P$进行两次$update$即可
3. 单点查询：求$A[i]$的值，即为$求P_i$的前缀和，对$P$进行$Sum$即可

代码：
upd、Sum函数同上
区间修改$:[l,r]$中的所有数$+x$

upd(l,x);
upd(r+1,-x);

单点查询:求$A[i]$的值

Sum(i);

3.区间修改，区间查询

P[]仍为A[]的差分数组，那么原数组的前缀和：
$A[1]+A[2]+\dots \dots +A[n]$
$=P[1]+(P[1]+P[2])+(P[1]+P[2]+P[3])+\dots \dots +(P[1]+P[2]+\dots \dots +P[n])$
$=n\ast P[1]+(n-1)\ast P[2]+(n-2)\ast P[3]+\dots \dots +P[n]$
$=n\ast (P[1]+P[2]+P[3]+\dots \dots +P[n])-(0\ast P[1]+1\ast P[2]+2\ast P[3]+\dots \dots +(n-1)\ast P[n])$
观察减式两边，分别将P[i]和(i-1)p[i]建立两个树状数组BIT1和BIT2，BIT1就是差分数组，区间修改按上一例进行；BIT2的增量就不是x了，而是x*(i-1)。至于区间查询，我们已经知道原数组前缀和了，直接相减即可查询区间和。
代码:

#include
#include
using namespace std;
int n;
int q;
long long BIT1[1000005],BIT2[1000005];
int a[1000005],p[1000005];
int lowbit(int x){
	return x & -x;
}
void upd(int k,int x){
	for(int i=k;i<=n;i+=lowbit(i)){
		BIT1[i]+=x, BIT2[i] += (long long)(k - 1) * x;
	}
}
long long Sum(int k){
	long long s=0;
	for(int i=k;i>=1;i-=lowbit(i)){
		s+=k*BIT1[i]-BIT2[i];
	}
	return s;
}
int main(){
	scanf("%d %d",&n,&q);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		p[i]=a[i]-a[i-1]; 
		upd(i,p[i]);
	}
	while(q--){
		int type;
		scanf("%d",&type);
		if(type==1){
			int l,r,x;
			scanf("%d %d %d",&l,&r,&x);
			upd(l,x);
			upd(r+1,-x);
		}
		else{
			int l,r;
			scanf("%d %d",&l,&r);
			printf("%lld\n",Sum(r)-Sum(l-1));
		}
	}
return 0;
} 

4.二维树状数组:单点修改，区间查询

思考一下二维前缀和以及普通前缀和的关系：