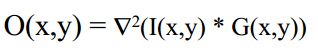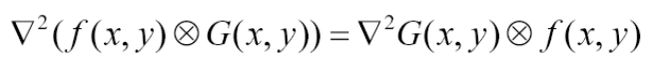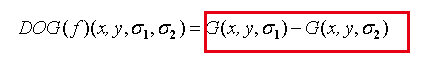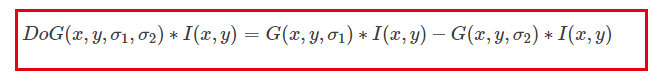【计算机视觉】Lecture 11:LoG和DoG滤波算子
今天的主题
高斯拉普拉斯 (LoG) 滤波算子
- 用于寻找边缘
- 也有助于寻找斑点!
使用高斯差分 (DoG) 来近似
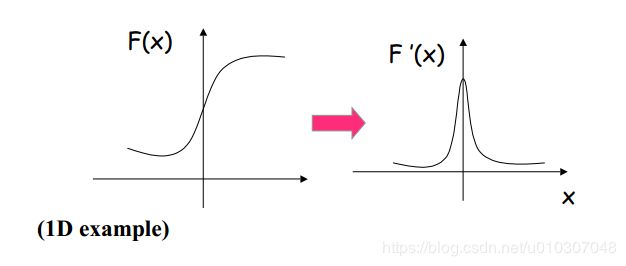
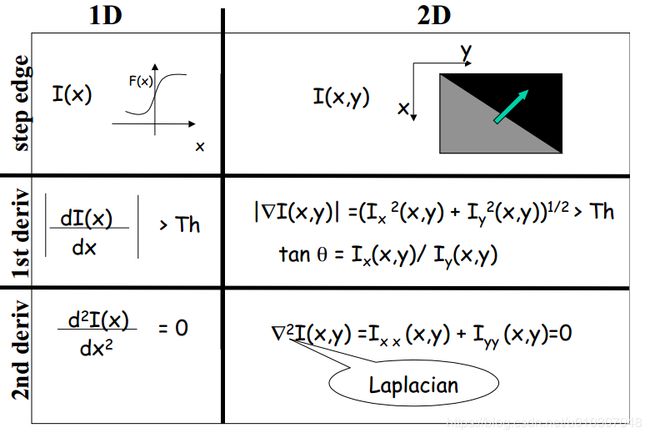
回忆:一阶导数滤波器
输入图像灰度的急剧变化对应于输入信号一阶导数的“峰或谷”
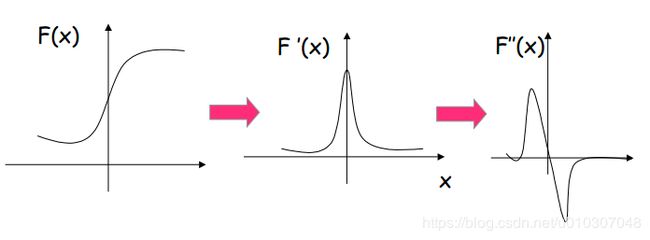
二阶导数滤波器
输入信号一阶导数的峰或谷对应于输入信号二阶导数的“零交叉点”。
数值导数
泰勒级数展开
中心差分近似于二阶导数
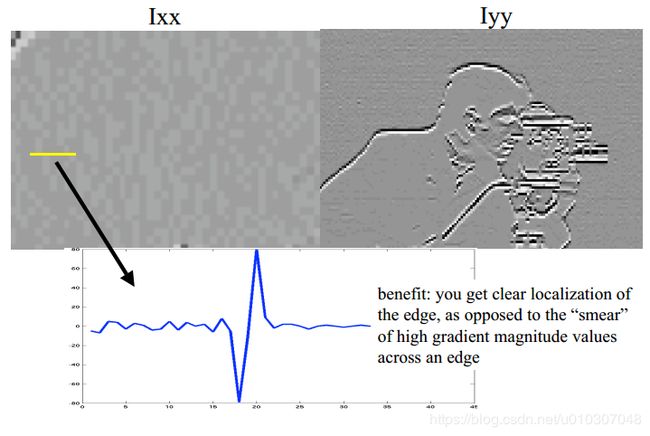
例子:二阶导数
优点:可以获得边缘的清晰定位,而不是边缘上高梯度幅值的“涂抹”
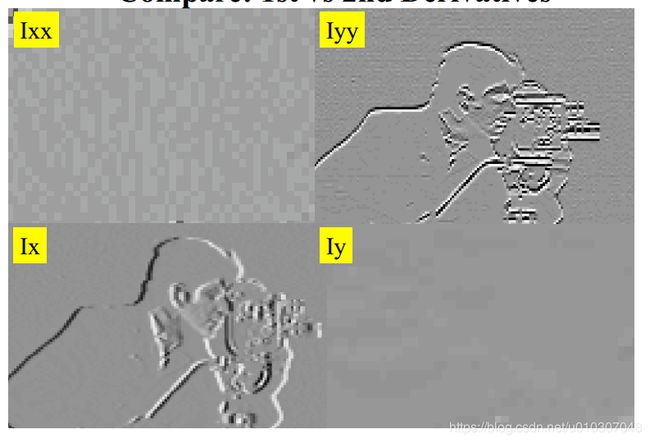
比较:一阶vs二阶导数
寻找零交叉点
在一阶导数中找到作为峰值的边缘的另一种近似方法是在二阶导数中找到零交叉点。
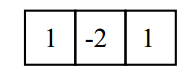
在一维面中,卷积 [1 -2 1] 并寻找响应(接近)为零的像素?
问题:当一阶导数为零时,二阶导数也为零。也就是说当与恒定灰度值区域卷积时,滤波器 [1 -2 1] 也产生零。
所以,在一维面中,用 [1 -2 1] 卷积并寻找响应接近于零且一阶导数的幅值“足够大”的像素。
边缘检测总结
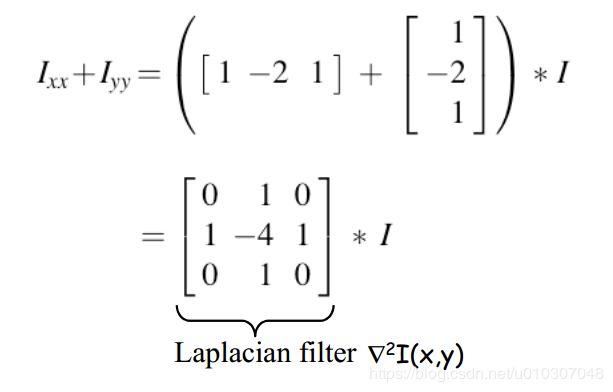
有限差分拉普拉斯
例子:拉普拉斯
关于拉普拉斯的注意点
![]() 是一个标量
是一个标量
优点:使用单个mask就可以获取
缺点:方向信息丢失
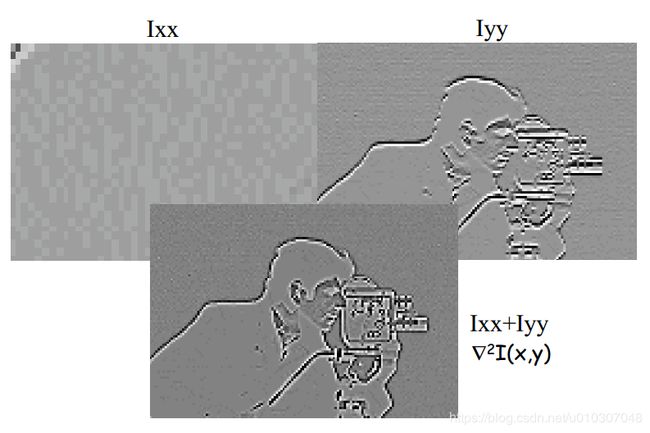
![]() 是两个维度二阶导数相加
是两个维度二阶导数相加
数值求导会放大噪声 (Lecture 4)
对噪声非常敏感
需要加滤波器
它总是与平滑操作相结合:先平滑(高斯滤波,来进行降噪处理,就形成了拉普拉斯高斯算子LoG(Laplace of Gaussian))再拉普拉斯
LoG滤波器
首先平滑 (高斯滤波器)
然后,找到零交叉点 (拉普拉斯滤波器)
也就是一个线性滤波器:
等式左边:高斯滤波图像的拉普拉斯变换(先高斯和图像卷积,然后求二阶导数)
等式右边:高斯的拉普拉斯变换 (LoG) 滤波图像(先高斯的二阶导数,然后卷积图像)
一维高斯和导数
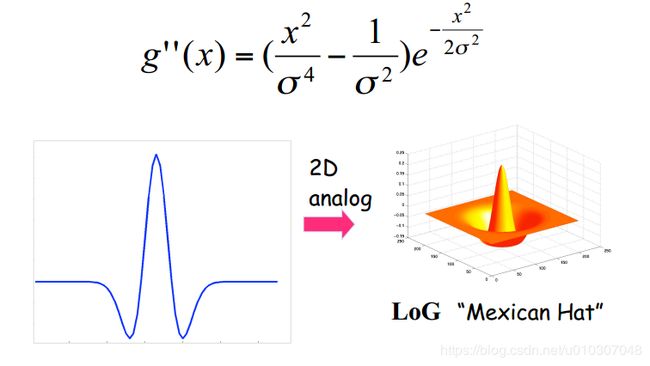
高斯的二阶导数
LoG算子的效果
带通滤波器(抑制高频和低频部分)
作为边缘检测器的零交叉点
原始零交叉点(无对比度阈值)
注意:闭合轮廓
你可能已经注意到零交叉点形成闭合轮廓
在地形图上考虑等高线
每一个都是一个闭合的轮廓
零交叉点是高度为0的等高线。
请记住,在我们的例子中,高度图是一个经过LoG滤波的图像——一个同时具有正和负“高度”的曲面
LoG的其他应用:Blob检测
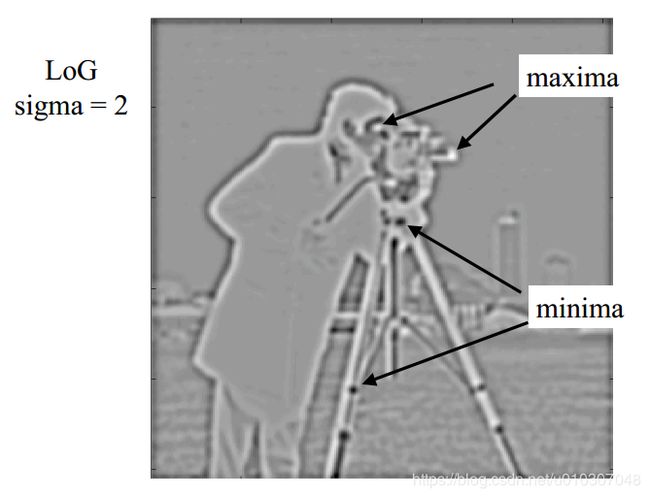
例子:LoG极值
LoG 斑点 (Blob) 检测
LoG滤波器极值定位 “blobs”:
极大值:亮背景上的暗斑点
极小值:暗背景上的亮斑点
斑点的尺度(大小,像素半径)由LoG滤波器的sigma参数确定
这个参数是从最前面的高斯滤波器来的,参数越大,则滤波器的范围越大,高斯滤波后就会更模糊。
观察和概括
LoG看起来有点像一只眼睛,它在眼睛区域的响应最大!
LoG:在亮的背景上看起来像是黑色的斑点
高斯导数(一阶导,前面加高斯):看起来像垂直和水平的阶跃边缘
回忆:使用滤波器的卷积(和互相关)可以被看作是将想要找到的内容与图像中的所有局部区域进行比较(卷积和互相关可以看作是找跟mask相似的块)。
关键思想:使用滤波器的互相关可以被看作是将想要找到的内容与图像中的所有局部区域进行比较(互相关可以看作是找跟mask相似的块)。
最大响应:亮背景上的暗斑点
最小响应:暗背景上的亮斑点
最大响应:垂直边缘;左侧较浅
最小响应:垂直边缘;右侧较浅
灰度的黑白就如同亮度的明暗,灰度值越高则图像越亮
有效实现 用DoG的LoG近似方法
LoG可以用两个不同尺度(不同Sigma)的高斯滤波器差(DoG)来近似
近似的LoG算子为:
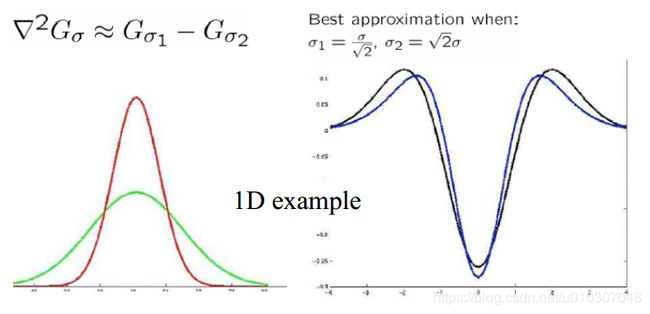
LoG可以用两个不同尺度(不同Sigma)的高斯滤波器差(DoG)来近似
高斯的可分解性和级联性可以适用于DoG,因此可以进行LoG算子的有效实现。
对图像进行两次高斯平滑再将结果相减就可以近似得到LoG作用与图像的效果了。
DoG近似也可以解释LoG的带通滤波作用(高斯是一个低通滤波器,一个低通减去另一个低通等于带通)
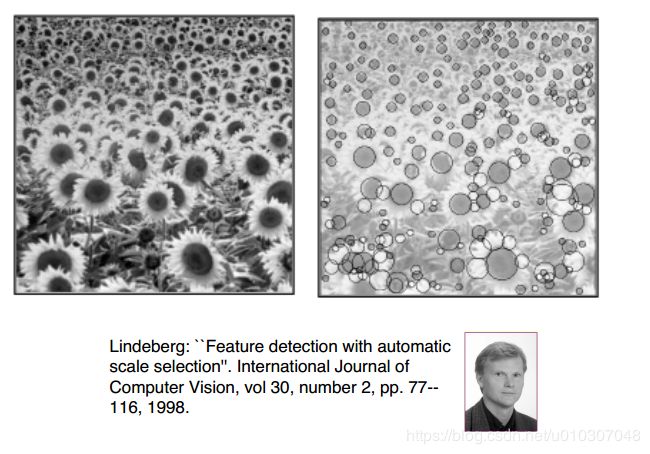
回到斑点检测
Lindeberg:斑点在LoG(或DoG)尺度空间体积内被检测为空间和尺度上的局部极值。
LoG的其他应用:斑点检测
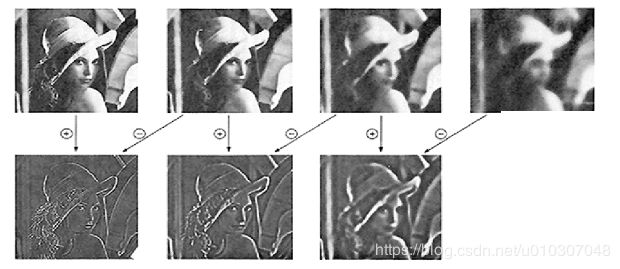
LoG的其他应用:图像编码
高斯金字塔的粗糙层预测下一个更精细层的显示。
虽然预测不准确,但意味着不必存储下一个精细尺度层的所有信息。
拉普拉斯金字塔储存了差异