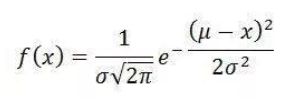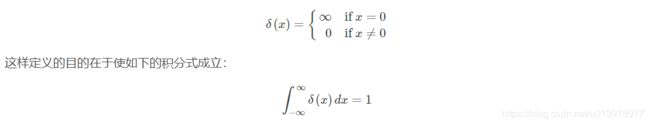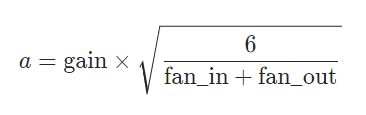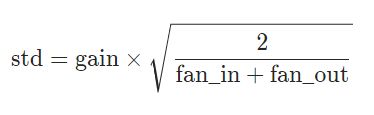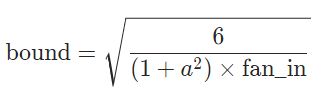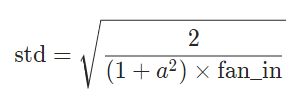Pytorch:参数初始化 笔记
一、参数初始化概述
在设计好神经网络结构之后,权重初始化方式会很大程度上影响模型的训练过程和最终效果。
权重初始化方式包括ImageNet预训练参数,kaiming_uniform方式以及多种权重初始化方式。这篇笔记主要记录一下Pytorch中内置的各种权重初始化方式的原理与使用。
神经网络中需要进行参数初始化操作的有Linear,Conv,BN等。
二、Pytorch中的参数初始化方法
2.1 不进行初始化操作,系统的默认初始化方法(来源于pytorch0.4源码)
Conv{1,2,3}d 都是继承于_ConvNd,其中对于参数的默认初始化方法如下:
def reset_parameters(self):
n = self.in_channels
for k in self.kernel_size:
n *= k
stdv = 1. / math.sqrt(n)
self.weight.data.uniform_(-stdv, stdv)
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)Linear
def reset_parameters(self):
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)BN{1,2,3}d 都是继承于_BatchNorm,其中对于参数的默认初始化方法如下:
def reset_parameters(self):
self.reset_running_stats()
if self.affine:
self.weight.data.uniform_()
self.bias.data.zero_()2.2 torch.nn.init.uniform_(tensor, a=0, b=1)
使用均匀分布U(a,b)初始化Tensor,即Tensor的填充值是等概率的范围为 [a,b) 的值。均值为 (a + b)/ 2.
w = torch.empty(2, 3)
nn.init.uniform_(w)
print(w)
'''
tensor([[0.8473, 0.3358, 0.0248],
[0.1876, 0.9774, 0.0559]])
'''2.3 torch.nn.init.normal_(tensor, mean=0, std=1)
高斯分布(Gaussian distribution),也称正态分布。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
w = torch.empty(2, 3)
nn.init.normal_(w)
print(w)
'''
tensor([[-1.9642, 1.0553, 1.0911],
[ 0.7136, 1.7050, 0.4172]])
'''2.4 torch.nn.init.constant_(tensor, val)
将Tensor填充为常量值。
w = torch.empty(2, 3)
nn.init.constant_(w, 0.3)
print(w)
'''
tensor([[0.3000, 0.3000, 0.3000],
[0.3000, 0.3000, 0.3000]])
'''2.5 torch.nn.init.eye_(tensor)
主对角线为1,其余元素为0。
w = torch.empty(2, 3)
nn.init.eye_(w)
print(w)
'''
tensor([[1., 0., 0.],
[0., 1., 0.]])
'''2.6 torch.nn.init.dirac_(tensor)
必须是{3, 4, 5}为tensor,使用Dirac delta function(狄拉克δ函数)进行初始化。
w = torch.empty(3,3,3)
nn.init.dirac_(w)
print(w)
'''
tensor([[[0., 1., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 1., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 1., 0.]]])
'''2.7 torch.nn.init.xavier_uniform_(tensor, gain=1)
“Understanding the difficulty of training deep feedforward neural networks” - Glorot, X. & Bengio, Y. (2010).
Using a uniform distribution. The resulting tensor will have values sampled from U(−a,a)
w = torch.empty(2,3)
nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('relu'))
print(w)
'''
tensor([[-0.4091, -1.1049, -0.6557],
[-1.0230, -0.4674, -0.4145]])
'''2.8 torch.nn.init.xavier_normal_(tensor, gain=1)
“Understanding the difficulty of training deep feedforward neural networks” - Glorot, X. & Bengio, Y. (2010)。
The resulting tensor will have values sampled from N(0,std)。
w = torch.empty(2,3)
nn.init.xavier_normal_(w)
print(w)
'''
tensor([[ 1.1797, -0.7723, -1.3113],
[ 0.3550, -0.3806, -0.5848]])
'''2.9 torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
“Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification” - He, K. et al. (2015)
The resulting tensor will have values sampled from U(−bound,bound):
w = torch.empty(2,3)
nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')
print(w)
'''
tensor([[ 1.1015, -1.2635, -0.8618],
[ 0.8951, -0.1690, 0.0104]])
'''2.10 torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
“Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification” - He, K. et al. (2015)
The resulting tensor will have values sampled from N(0,std)
w = torch.empty(2,3)
nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')
print(w)
'''
tensor([[ 0.0952, 0.0116, -0.4601],
[-2.4272, -1.7924, 1.3828]])
'''三、Pytorch权重初始化方法
3.1 使用For循环进行权重初始化
net = MyNet()
for m in net.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)3.2 使用Apply函数进行权重初始化
def weights_init_kaiming(m):
classname = m.__class__.__name__
# print(classname)
if classname.find('Conv') != -1:
init.kaiming_normal(m.weight.data, a=0, mode='fan_in')
elif classname.find('Linear') != -1:
init.kaiming_normal_(m.weight.data, a=0, mode='fan_out')
init.constant_(m.bias.data, 0.0)
elif classname.find('BatchNorm1d') != -1:
init.normal_(m.weight.data, 1.0, 0.02)
init.constant_(m.bias.data, 0.0)
def weights_init(m):
if isinstance(m, nn.Conv2d):
xavier(m.weight.data)
xavier(m.bias.data)
net=MyNet()
# apply函数会递归地搜索网络内的所有module并把参数表示的函数应用到所有的module上。
net.apply(weights_init_kaiming)
net.apply(weights_init)
参考
- https://ptorch.com/docs/8/torch-nn-init
- https://blog.csdn.net/u011668104/article/details/81670544