机器学习入门04——糖尿病数据预测

利用Logistic回归技术实现糖尿病发病预测

数据说明

数据说明： Pima Indians Diabetes Data Set（皮马印第安人糖尿病数据集） 根据现有的医疗信息预测5年内皮马印第安人糖尿病发作的概率。
数据链接：https://archive.ics.uci.edu/ml/datasets/Pima+Indians+Diabetes
p.s.: Kaggle也有一个Practice Fusion Diabetes Classification任务，可以试试:)
https://www.kaggle.com/c/pf2012-diabetes

1)文件说明

pima-indians-diabetes.csv：数据文件

2)字段说明

数据集共9个字段:
pregnants：怀孕次数
Plasma_glucose_concentration：口服葡萄糖耐量试验中2小时后的血浆葡萄糖浓度
blood_pressure：舒张压，单位:mm Hg
Triceps_skin_fold_thickness：三头肌皮褶厚度，单位：mm
serum_insulin：餐后血清胰岛素，单位:mm
BMI：体重指数（体重（公斤）/ 身高（米）^2）
Diabetes_pedigree_function：糖尿病家系作用
Age：年龄
Target：标签， 0表示不发病，1表示发病

第一步 特征工程

对于原始数据的处理使用了一下几个方法：

• 使用中值补充缺失数据
• 使用StandardScaler()对数据进行标准化处理
• 保存为csv格式

import numpy as np
import pandas as pd
#input data
train = pd.read_csv("pima-indians-diabetes.csv")
print(train.head())

#查看缺失值较多的数据统计
NaN_col_names = ['Plasma_glucose_concentration','blood_pressure','Triceps_skin_fold_thickness','serum_insulin','BMI']
train[NaN_col_names] = train[NaN_col_names].replace(0, np.NaN)
print(train.isnull().sum())


#中值补充确实值
medians = train.median() 
train = train.fillna(medians)

print(train.isnull().sum())


#  get labels
y_train = train['Target']   
X_train = train.drop(["Target"], axis=1)

#用于保存特征工程之后的结果
feat_names = X_train.columns

# 数据标准化
from sklearn.preprocessing import StandardScaler

# 初始化特征的标准化器
ss_X = StandardScaler()

# 分别对训练和测试数据的特征进行标准化处理
X_train = ss_X.fit_transform(X_train)

#存为csv格式
X_train = pd.DataFrame(columns = feat_names, data = X_train)

train = pd.concat([X_train, y_train], axis = 1)

train.to_csv('FE_pima-indians-diabetes.csv',index = False,header=True)

print(train.head())

第二步 训练模型

训练模型主要分为以下几个步骤：

• 导入数据
• 分别使用L1正则和L2正则训练模型
• 使用5折交叉验证
• 使用log似然损失和正确率对模型进行超参数调优
• 绘制CV误差曲线

# 首先 import 必要的模块
import pandas as pd 
import numpy as np

from sklearn.model_selection import GridSearchCV

import matplotlib.pyplot as plt

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
#%matplotlib inline


# 读取数据

train = pd.read_csv('FE_pima-indians-diabetes.csv')

y_train = train['Target']   
X_train = train.drop(["Target"], axis=1)

#保存特征名字以备后用（可视化）
feat_names = X_train.columns 

#需要调优的参数
# 请尝试将L1正则和L2正则分开，并配合合适的优化求解算法（slover）
penaltys = ['l1','l2']

#训练数据多，C可以大一点（更多相信数据）
Cs = [0.01, 0.1, 1, 10, 100, 1000, 10000]

tuned_parameters = dict(penalty = penaltys, C = Cs)#组合调优参数

lr_penalty= LogisticRegression()
#grid= GridSearchCV(lr_penalty, tuned_parameters,cv=5, scoring='neg_log_loss')#log似然损失
grid= GridSearchCV(lr_penalty, tuned_parameters,cv=5, scoring='accuracy')#正确率
grid.fit(X_train,y_train)

# examine the best model
print(-grid.best_score_)#打印模型参数
print(grid.best_params_)


#绘制CV误差曲线分析模型
# plot CV误差曲线
test_means = grid.cv_results_[ 'mean_test_score' ]
test_stds = grid.cv_results_[ 'std_test_score' ]
train_means = grid.cv_results_[ 'mean_train_score' ]
train_stds = grid.cv_results_[ 'std_train_score' ]


# plot results
n_Cs = len(Cs)
number_penaltys = len(penaltys)
test_scores = np.array(test_means).reshape(n_Cs,number_penaltys)
train_scores = np.array(train_means).reshape(n_Cs,number_penaltys)
test_stds = np.array(test_stds).reshape(n_Cs,number_penaltys)
train_stds = np.array(train_stds).reshape(n_Cs,number_penaltys)

x_axis = np.log10(Cs)
for i, value in enumerate(penaltys):
    #pyplot.plot(log(Cs), test_scores[i], label= 'penalty:'   + str(value))
    plt.errorbar(x_axis, -test_scores[:,i], yerr=test_stds[:,i] ,label = penaltys[i] +' Test')
    #plt.errorbar(x_axis, -train_scores[:,i], yerr=train_stds[:,i] ,label = penaltys[i] +' Train')
    
plt.legend()
plt.xlabel( 'log(C)' )                                                                                                      
plt.ylabel( 'logloss' )
plt.savefig('LogisticGridSearchCV_C.png' )

plt.show()

import cPickle

cPickle.dump(grid.best_estimator_, open("FE_pima-indians-diabetes", 'wb'))

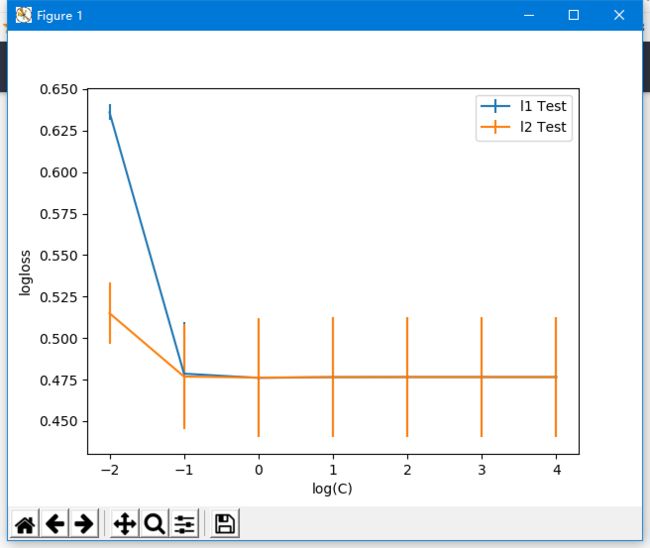
使用log似然损失对Logistic回归模型的正则超参数调优

参数结果：

0.47602775434873434
{'C': 1, 'penalty': 'l1'}

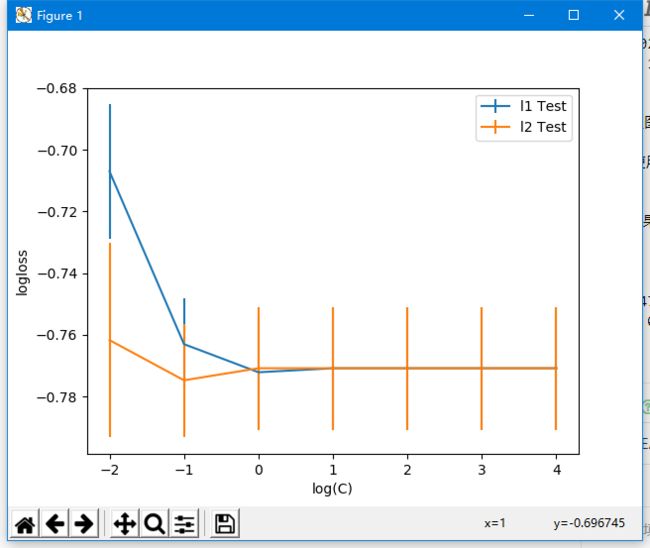
使用log似然损失对Logistic回归模型的正则超参数调优

参数结果：

-0.7747395833333334
{'C': 0.1, 'penalty': 'l2'}

可以看到，使用正确率和l2正则对Logistic回归模型的正则超参数调优可以使损失函数最小

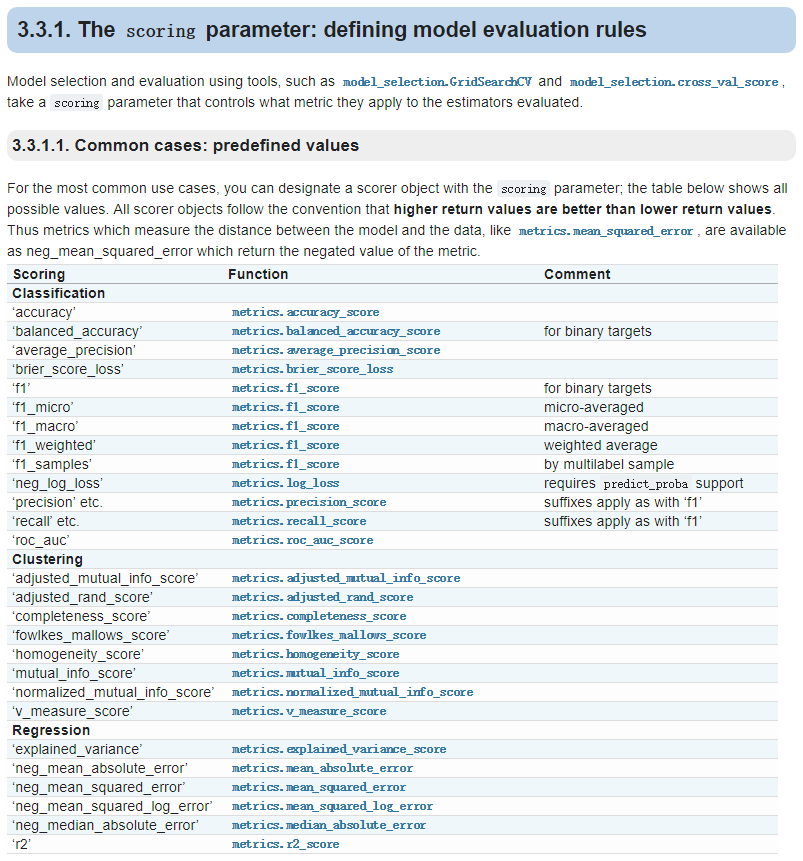
GridSearchCV(）中scoring的值可以选用一下参数：

点击这里可以到官网查看！！！

项目源代码：糖尿病发病率预测