《Practice on Long Sequential User Behavior Modeling for Click-Through Rate Prediction》
前言
因为需要处理不定长的行为序列,找到了这篇KDD2019文章。
Title:《Practice on Long Sequential User Behavior Modeling for Click-Through Rate Prediction》
ref:https://arxiv.org/abs/1905.09248
code:https://github.com/UIC-Paper/MIMN/
这个仓库还把阿里妈妈UIC的几个前置工作(DIN,DIEN)的代码都放上去了,都是用tf写的。
原论文写的有点不清楚,具体原理需要自己额外看NTM(神经图灵机)的论文才能充分理解。
1 阿里原论文
读写部分简单,略过。
1.1 Memory Utilization Control
根据定义, g t = ∑ c = 1 t w c w ~ g_t = \sum_{c=1}^{t} w_{c}^{\widetilde{w}} gt=∑c=1twcw
也就是说,计算 g t g_{t} gt需要知道 w t w ~ w_{t}^{\widetilde{w}} wtw 。
根据公式(6),计算 w t w ~ w_{t}^{\widetilde{w}} wtw 又需要知道 P t P_t Pt。
根据公式(5),计算 P t P_t Pt需要知道 g t g_t gt。
这不是死循环了吗?
大哥这怎么求解?
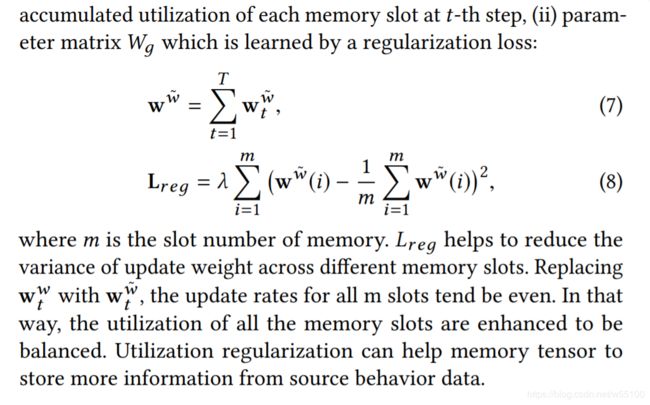
W g W_g Wg是一个自定义的可训练参数,用来计算 w t w ~ w_{t}^{\widetilde{w}} wtw ,
而最终 w t w ~ w_{t}^{\widetilde{w}} wtw 会用来计算 L o s s r e g Loss_{reg} Lossreg,
所以会随着 L o s s r e g Loss_{reg} Lossreg在训练时得到更新。
1.2 Memory induction Unit
MIN部分是为了弥补普通NTM无法习得high-order信息的遗憾。
MIN内部也有一个记忆矩阵S,形状与NTM中的那个一模一样,也是m个slot。
本部分采用GRU单元。
在时刻t,
计算前文提过的NTM里的那个 w t r w_{t}^{r} wtr,形状(m),每个值对应一个槽。
然后从中取得topK个值的index,这些index分别对应一个记忆槽。
对选中的某个index i,执行,
S t ( i ) = G R U ( S t − 1 ( i ) , M t ( i ) , e t ) , 公式 ( 9 ) S_t(i)=GRU(S_{t-1}(i),M_t(i),e_t) \text{, 公式} (9) St(i)=GRU(St−1(i),Mt(i),et), 公式(9)
注意这里的 M t ( i ) M_t(i) Mt(i)也是前文NTM里的。
e t e_t et是embd后的行为向量。
根据公式(9)就可以知道,MIN部分的记忆矩阵S,融合了来自原始行为的信息和NTM记忆池中存储的信息,2部分。
2 神经图灵机
阿里这个作者写的属实不清不楚,为了弄明白原理,只能去找
神经图灵机原论文(https://arxiv.org/abs/1410.5401)。
define
Neural Turning Machine,NTM
由2个component组成,controller与memory bank。
由若干heads链接controller与memory。
其中memory的形状为(N,M)。
heads包含2个类别,read head与write head。
每个类别的head可以有≥1个。
Heads emit outputs that determine the memory locations to interact with.
w t w_t wt defines to which degree the heads read or write at each location.
(注:此处memory location等价于阿里论文里的memory slot)
2.1 Read
写成矩阵运算形式。
在time t,每个read head产出一个 w t r , s h a p e = ( N ) w_t^r,shape=(N) wtr,shape=(N)
最终返回的read-vector公式为:
r t = w t ⊙ M t r_t=w_t \odot M_t rt=wt⊙Mt
s h a p e : ( M ) = ( N ) ⊙ ( N , M ) shape:(M) = (N)\odot (N,M) shape:(M)=(N)⊙(N,M)
2.2 Write
在time t,每个write head产出:
① w t w , s h a p e = ( N ) ① w_t^w,shape=(N) ①wtw,shape=(N)
② e t , s h a p e = ( M ) ② e_t,shape=(M) ②et,shape=(M)
③ a t , s h a p e = ( M ) ③ a_t,shape=(M) ③at,shape=(M)
对memory的write,总是执行先减后加。
2.2.1 firstly, sub part
写成矩阵运算形式。
M ~ t = M t − 1 ⋅ [ 1 − w t ⊗ e t ] \widetilde{M}_t=M_{t-1} \cdot [\bold{1}-w_t \otimes e_t] M t=Mt−1⋅[1−wt⊗et],其中 1 为 全 1 矩 阵 \bold{1}为全1矩阵 1为全1矩阵, 运 算 符 ⋅ 表 示 点 乘 运算符\cdot表示点乘 运算符⋅表示点乘。
s h a p e : ( N , M ) = ( N , M ) ⋅ [ ( N , M ) − ( N ) ⊗ ( M ) ] shape:(N,M)=(N,M)\cdot[(N,M)-(N)\otimes (M)] shape:(N,M)=(N,M)⋅[(N,M)−(N)⊗(M)]。
2.2.2 secondly,add part
写成矩阵运算形式。
M t = M ~ t + w t ⊗ a t M_t = \widetilde{M}_t + w_t \otimes a_t Mt=M t+wt⊗at
s h a p e : ( N , M ) = ( N , M ) + ( N ) ⊗ ( M ) shape:(N,M) = (N,M)+(N)\otimes (M) shape:(N,M)=(N,M)+(N)⊗(M)
2.2.3 补充说明
按论文里的说法,multi-heads存在时,所谓的"先减后加”,指的是将所有write heads的sub都做完,再把所有heads的add都加上。
上述规则的好处在于,如此一来,多个write heads之间的顺序关系就不重要了。
因为是把所有sub都做完,而此处sub的本质是点乘运算,显然右边的多个系数矩阵可以任意交换次序不影响最终结果。
同理在做所有add的时候,加法项任意交换次序不影响最终结果。
但是
我在github上看到的开源实现,似乎均没有遵守这一原则。
例如这个仓库https://github.com/loudinthecloud/pytorch-ntm
作者的写法是有n对heads时,每对依次read,write,read,write。

从更新公式来看,这种写法,就与顺序相关了。
这n对heads,一旦改变顺序必然改变结果。
3 实现思路
虽然开源的实现没有遵循order-free 的原则,但基本的代码框架已经搭好了。
我看了一下有几个细节需要再修改一下,
- memory不需要丢给head做属性,head的唯一作用不过是产出需要的几个 w t , e t , a t w_t,e_t,a_t wt,et,at,读写过程的调用可以再上调一层。
- 遵循order-free原则,修改流程
- 我现在需要用到NTM的项目,input是不定长的序列,因此不能用开源代码里的定长方案,需要修改为支持不定长序列运算的方案。
关于支持不定长序列。这个很复杂。
他原来的方案,每次input是(bz,input_dim)。
这个本质上是(bz,1,input_dim),即每次其实只输入了一个时间t。
然后需要循环len_seq次,才能把总的(bz,len_seq,input_dim)的数据更新完。
最后输入一次 torch.zeros(bz,input_dim) 去查询最终特征。
但是在我现在的数据集上,对不同的bz(i),其len_seq(i)并不相同。
因此原来等长的矩阵运算就不能做了。
有一种思路是padding 0 到等长。
但这样做对于模型的效果是未知的。
模型能否把0当成一种无意义的输入,从而把 e t = 0 , a t = 0 e_t=0,a_t=0 et=0,at=0,使得既不遗忘,也不更新,这是我无法控制的事情。
甚至可以预见很大概率上,即便输入全0,也不能做到不遗忘不更新。
过去的纯矩阵运算是可以用mask来解决padding0的不确定行为问题。
但这个模型的序列特性导致要这么做会非常非常麻烦。
我只好用比较蠢的办法,一个一个算了。
先不考虑batch。
一个序列行为List[ embd_vector ] , shape=(lenseq,embd_size)
每次输入一个time step,也就是(embd_size)向量。
此时更新的步骤为。
#伪代码,仅供参考
init_state = {
'last_read':torch.rand(n_heads*M),#每个read头返回一个(M)形状的结果$r_t$
'last_control': torch.rand(n_lstm_layers,bz=1,hidden_size),#采用lstm作为controller的核心结构,也可以改成别的单元,做对应调整即可。
'last_head':torch.randn(2*n_heads,M) #n_heads对读写头,2*n_heads个头,每个头返回一个(M)形状的权重$w_t$
}
cur_input = torch.cat([x,state['last_read']],dim=0)
cur_control_out, state['last_control'] = self.controller(cur_input,state['last_control')
#简单点,假设就一对读写头。
r_t, w_read = readhead(cur_control_out, state['last_head'][0])
w_write = head(cur_control_out, state['last_head'][1])
state['last_read'] = r_t
state['last_head'] = torch.cat([w_read,w_write],dim=1) #(2,M)
reads=[]
reads.append(r_t)
#最终提取到的,step t的特征为control的输出与read的输出拼接
cur_feature = torch.cat([cur_control_out]+reads)
return cur_feature,state
补充
现在可以解释在阿里这篇论文中遇到的几个问题了。
- g t g_t gt的计算是否出现套娃?不会,根据原论文的想法,在t时刻的 g t g_t gt应该[0,t-1]时刻的状态累加,其中0时刻是一个初始变量。阿里论文里标出[0,t]的累加属于行文错误。
- 在阿里论文中 w g w_g wg现在是一个自定义的可训练参数矩阵了,用于平衡t时刻为止所有位置已被使用的量,这与NTM论文里的 w t g w_t^g wtg需要做区分。
#参考:https://blog.csdn.net/ppp8300885/article/details/80383246
