机器学习（三）：拉格朗日乘子与梯度下降法

这里介绍两个在以后的机器学习算法中经常使用的技巧：拉格朗日乘子（Lagrange multiplier）和梯度下降法（Gradient descent）。

1. 拉格朗日乘子法

拉格朗日乘子被⽤于寻找多元变量在⼀个或者多个限制条件下的驻点。

1.1 等式约束条件

考虑这样一个问题：
求解 f(x1,x2) 的最大值，其中x1和x2必须满足如下限制条件: g(x1,x2)=0 。

求解方法1：将 g(x1,x2)=0 转化为 x2=h(x1) 带入f函数，然后使用微分法求解驻点 x∗1 ，然后得到驻点 x∗2=h(x∗1) 。
这种⽅法的⼀个问题是，把x2显式地表⽰为x1的函数，即找到限制⽅程的解析解很困难。并且，这种⽅法把x1和x2区别对待，这破坏了这些变量之间⾃然存在的对称性。

由此我们引入拉格朗日乘子法。

1.1.1 约束条件 g(x)=0 的特性

设向量 x∈RD ，则 g(x)=0 表示一个D-1维的曲面。
有

∇g(x)正交于此曲面

证明： 考虑⼀个位于限制曲⾯上的点x以及这个点附近同样位于曲⾯上的点x + ϵ。如
果我们在点x处进⾏泰勒展开，那么我们有

g(x+ϵ)≈g(x)+ϵT∇>g(x)

我们有：

g(x+ϵ)=g(x)=0⇒ϵT∇g(x)>≈0

ϵ→0⇒ϵT∇g(x)=0

ϵ 平行于曲面，所以 ∇g(x) 正交于曲面。

1.1.2 原问题转化为拉格朗日函数

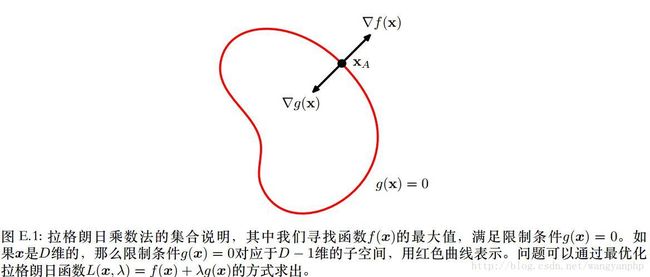
在g(x)=0上寻找一个 x∗ ,使得f(x)最大。必然有 ∇f(x∗) 正交于限制曲面。

证明：

f(x∗+ϵ)≈f(x∗)+ϵT∇f(x∗)

如果 ∇f(x∗) 不正交于限制曲面，则必然存在 ϵ≠0 使得 ϵT∇f(x∗)>0 ，则 x∗ 就不再是驻点。

所以对于驻点， ∇f//∇g ，所以必然有： ∇f+λ∇g=0 。
其中 λ≠0 被称为拉格朗⽇乘数（ Lagrange multiplier）。注意， λ的符号任意。
由此我们定义拉格朗日函数：

L(x,λ)=f(x)+λg(x)

驻点可由 ∇xL=0 求得。

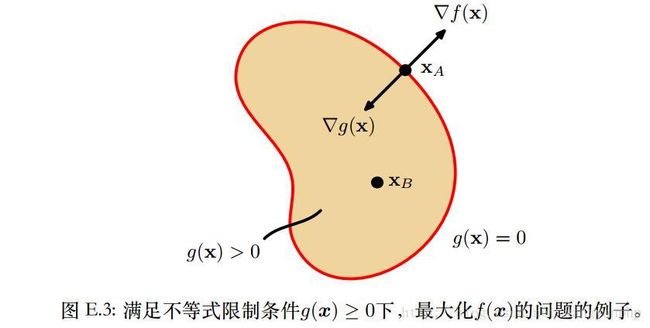
1.2 不等式约束条件

考虑在 g(x)≥0 下，f(x)的驻点。

• 如果驻点位于g(x)>0上，驻点只有一种可能 ∇f=0 ，此时g(x)不起作用，也即拉格朗日函数L中λ=0；
• 如果驻点位于g(x)=0上，那么此问题等同于上述的等式约束条件。有所不同的是， ∇f 必然指向 g(x)<0 的方向，也即：对于λ>0，有 ∇f=−λ∇g 。
  上述两种情况都会导致 λg(x)=0
  因此在限制条件g(x) ≥ 0下最⼤化f(x)的问题的解可以通过下⾯的⽅式获得：
  
  L(x,λ)=f(x)+λg(x)
  
  限制条件为：
  
  g(x)≥0
  λ≥0
  λg(x)=0
  被称为KKT条件。

2. 梯度下降法

2.1梯度下降法原理

梯度下降法（gradient descent）或最速下降法（steepest descent）是求解无约束最优化问题的一种常用方法。
问题描述：假设 f(x),x∈RD 上具有一阶连续偏导数，要求解使得f(x)取最小值的点x*。

梯度下降法是一种迭代算法。选取适当的初值 x0 ，不断迭代更新x，进行目标函数的最小化，直到收敛。
假设第t次迭代值为 xt ，如何得到 xt+1 呢？
假设 xt+1 是 xt 向某一方向v（v是单位向量）移动了 η 长度，则我们希望在给定长度 η 下，选取一个方向， f(xt+1 下降最多，也即：

min||v||=1f(xt+ηv)=f(xt)+ηvT∇f(xt)

我们很容易得到：当方向v与 ∇f(xt) 完全相反时， f(xt+1) 下降最快。
也即：

v=−∇f(xt)||∇f(xt)||

这样会产生什么效果呢？

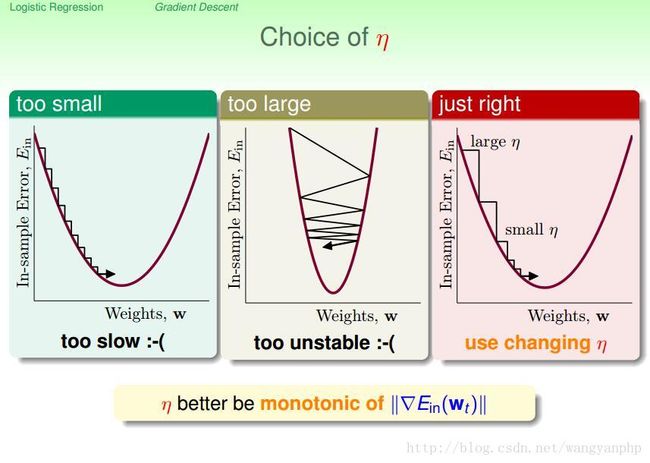
当 η 太小时，梯度下降算法会很慢；如果 η 太大，那么算法会不稳定。好的方法是：当梯度比较平缓时，η小一点；当梯度比较陡时，η大一点。也即η与 ∇f(xt) 成正比。
使：

η=λ||∇f(xt)||

有：

xt+1=xt+ηv=xt+λ||∇f(xt)||⋅−∇f(xt)||∇f(xt)||=xt−λ∇f(xt)

2.2 梯度下降法步骤

1. 取初始值 x0 ，t=0；
2. 计算 f(xt)，∇f(xt) ，如果 ||∇f(xt)||<ϵ ，停止迭代，令 x∗=xt ；否则 xt+1=xt−λ∇f(xt) 。
3. 计算 f(xt+1) ，如果 ||f(xt+1)−f(xt)||<ϵ or ||xt+1−xt||<ϵ 时，停止迭代，令 x∗=xt+1 。
4. 否则，置t=t+1；转步骤2。

说明：
1. 我们也可以不指定λ，而是每次在步骤2中计算λ，其中λ为： minλ≥0f(xt−λ∇f(xt)) 。
2. 当目标函数是凸函数时，梯度下降法的解是全局最优解；一般情况下，其解不保证是全局最优解。

2.3 梯度下降的使用策略

2.3.1 Scaling

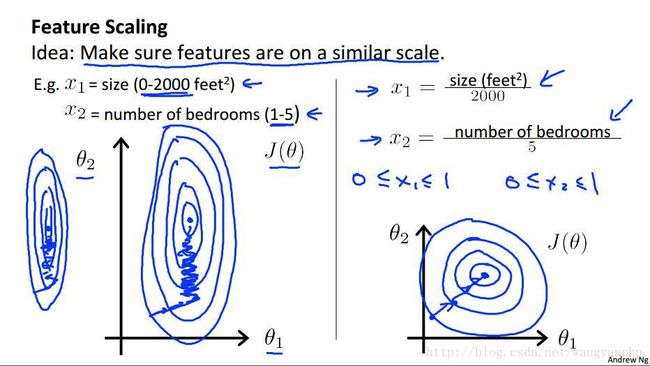
如上图，假设有两个feature：x1和x2。如果直接做梯度下降的话，效果如左图：效率会很低。我们通常是将feature变换为 −1≤xi≤1 ，当然也没有固定的限制，只要feature大体上变得在同一范围之间即可。大小相差3倍左右是可以接受的。譬如： −3≤xi≤3 或 −13≤xi≤13 。
我们经常进行均值归一化：

2.3.2 确保梯度下降法正确的工作

如何确保其正确的工作，当我们运行梯度下降算法时，我们需要观察 Ein 是否随着迭代次数下降：

J与迭代次数的正确关系如上图所示，我们可以通过上图确定合理的迭代次数。如果需要迭代次数太多，也即下降太慢，则说明学习速率太低，需要用更大的学习速率。

那么异常情况是什么呢？

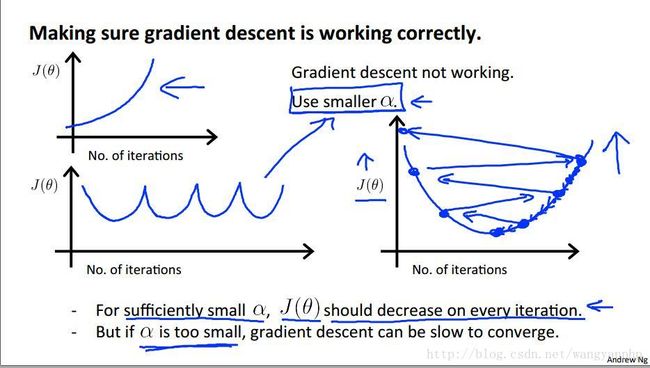
如上图，损失函数J并不随着迭代次数递减，这说明学习速率过大，需要用更小的学习速率。

通常情况下，我们会试验多个不同的学习速率λ，选择合适的学习速率：

2.4 梯度下降的其他变式

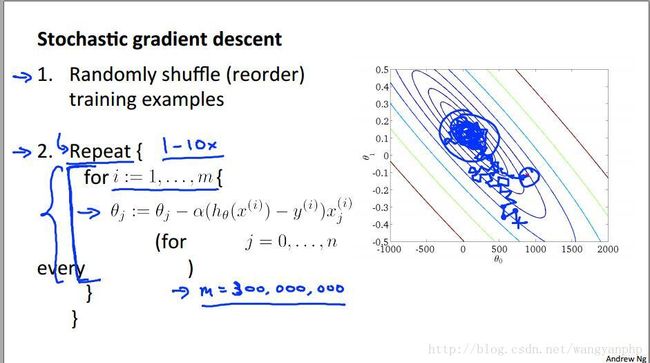
2.4.1 随机梯度下降法

考虑如下算法：

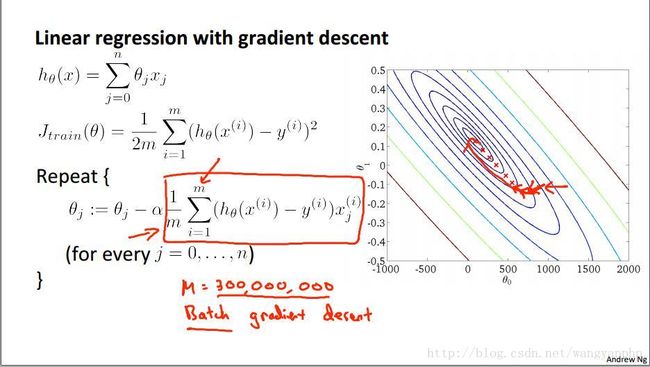
我们使用梯度下降算法进行线性回归。假设training set有3亿数据，那么每次迭代，对于每一个特征参数，都需要对3亿个数据同时进行运算，这样做的效率太低。

我们仔细观察上式中梯度 1m∑mi=1(h(x(i)−y(i))x(i) ，它是由m个数据平均而来的，我们设

∇j(θ,x(i),y(i))=(h(x(i)−y(i))x(i)

将所有的m个点视为整体，则有：

∇J(θ)=E(∇j(θ,x(i),y(i)))

这一关系就是随机变量中样本点与期望之间的关系，有：

∇j(θ,x(i),y(i))=∇J(θ)+variance

我们完全可以随机选择一个点来近似梯度，而不是每次计算都使用所有点：

2.4.2 Mini-batch 梯度下降法

根据随机梯度的思路，我们很容易的就能有mini-batch梯度的想法：
在梯度计算中，将m视为总体，是随机选取某个样本来估计 ∇J(θ) 好，还是选取b个样本来估计 ∇J(θ) 好？根据Hoeffding定理很容易得出结论。