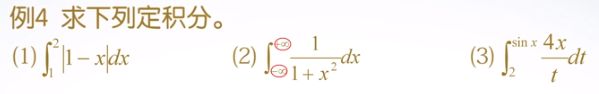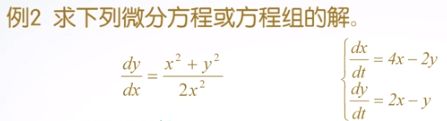Matlab学习之—符号计算

慕课地址

7.1 符号对象

7.1.1 符号对象的建立

sym函数

符号计算的结果是一个精确的数学表达式，更像是一种符号推演，结果是完全精确的。
数值计算的结果是一个数值，是近似解。

syms命令

7.1.2 符号对象的运算

syms x;
f = 2*x^2 +3*x-5;
g = x^2+7;
f+g

结果：

3*x^2 + 3*x + 2

syms x;
assume(x<0);
abs(x) == x

结果

ans =
	-x == x

assume(x,'positive');
abs(x) ==x

结果

ans = 
x == x

两种方式得到的结果完全相同。

syms a b;
s = a^3 - b^3;
factor(s)

结果

ans = 
 	[ a - b, a^2 + a*b + b^2]

factor (12)

结果

ans =
     2     2     3

%梅森素数的验证问题。请验证M19 、 M23 、 M29 、 M31是否为梅森素数。
syms p;
m=2^p-1;   %定义梅森数的公式
p=19;
m19=eval(m)  %求M19的值
factor(m19)  %验证是否为素数

p=23;
m23=eval(m)
factor(m23)

p=29;
m29=eval(m)
factor(m29)

p=31;
m31=eval(m)
factor(m31)

结果：
M19 M31是梅森素数，M23和M29不是。

%例1 求方程ax^2+bx+c=0的根。
syms a b c x;
f=a*x^2+b*x+c
g=coeffs(f,x)  %提取表达式系数，系数从低次到高次
g=g(end:-1:1)  %反转系数矩阵，由高次到低次排列
roots(g)   %调用求根公式

7.1.3 符号矩阵

syms a b x y alp;
m = [a^3-b^3, sin(alp)^2+cos(alp)^2;(15*x*y-3*x^2)/(x-5*y),78]

m = 
[                    a^3 - b^3, cos(alp)^2 + sin(alp)^2]
[ (- 3*x^2 + 15*y*x)/(x - 5*y), 

化简

simplify(m)

ans =
[ a^3 - b^3,  1]
[      -3*x, 78]

由于符号矩阵也是一个矩阵，所以有关矩阵的运算对符号矩阵也仍然适用，前面介绍过的点运算符和相关函数，如diag inv det rank trace等等都可以直接应用于符号矩阵。

%例2 当λ取何值时，以下齐次线性方程组有非零解。
syms lamda;
A=[1-lamda,-2,4;2,3-lamda,1;1,1,1-lamda];
D=det(A);
factor(D)

结果

ans =
[ -1, lamda, lamda - 2, lamda - 3]

从而得知，当 $\lambda$=0、 $\lambda$=2或 $\lambda$=3时，原方程组有非零解。

7.2 符号微积分

7.2.1 符号函数的极限

%例1 求下列极限。
%（1）
syms a m x n;
f=(x^(1/m)-a^(1/m))/(x-a);
limit(f,x,a) 

结果

ans =
	a^(1/m - 1)/m

% （2）
g=(1+1/n)^n;
limit(g,n,inf)

结果

ans = 
	exp(1)   %自然常数e

7.2.2 符号函数的导数

在符号函数的变量多于一个的情况下，diff函数也可以用于求偏导数。

%例2 求下列函数的导数。
（1）
syms  x y z;
f=sqrt(1+exp(x));
diff(f)  % 默认求x的一阶导数 

ans =
	exp(x)/(2*(exp(x) + 1)^(1/2))

（2）
g=x*exp(y)/y^2;
diff(g,x)   % 求g关于x的一阶偏导数
            
diff(g,y)    % 求g关于y的一阶偏导数

ans =
	exp(y)/y^2
ans =
	(x*exp(y))/y^2 - (2*x*exp(y))/y^3

极限、导数、微分的概念是紧密关联的。有极限是可导的前提，而导数是微分之商，因此导数也称为微商。

7.2.3 符号函数的积分

不定积分

h = 3*x
int (h)

ans = 
(3*x^2)/2

%例3 求下列不定积分。
(1)
syms x t;
f=(3-x^2)^3;
int(f)

ans =
	- x^7/7 + (9*x^5)/5 - 9*x^3 + 27*x

%(2)
g=5*x*t/(1+x^2);
int(g,t)   %如果不指定变量将以x作为主变量进行积分

ans =
	(5*t^2*x)/(2*(x^2 + 1))

定积分

%例4 求下列定积分。
%（1）
syms x t;
int(abs(1-x),1,2)

ans =
	1/2

%（2）
int(1/(1+x^2),-inf,inf)

ans =
 	pi

%（3）
int(4*x/t,t,2,sin(x))

ans =
	4*x*(log(sin(x)) - log(2))  %符号函数

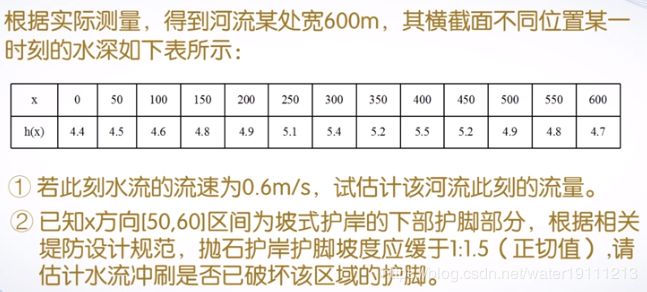
%河道水流量的估算问题。
%(1)
xi=0:50:600;
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7];
p=polyfit(xi,yi,3); %曲线拟合
plot(xi,yi,'o',xi,polyval(p,xi)); 
syms y x;
y=poly2sym(p,x);  %拟合曲线的多项式形式转化为符号表达式
s=int(y,x,0,600); %计算横截面面积    
v=s*0.6;          %计算水流量    
eval(v)           %1787.4（m3/s）

%（2）
yn=-yi;  %曲线倒转，是的拟合曲线方向与实际相符合
p=polyfit(xi,yn,3);
plot(xi,yn,'o',xi,polyval(p,xi));
syms y x yii;
y=poly2sym(p,x);
yii=diff(y,x); 
x=50:60;                                    
k=eval(yii);                                
all(abs(k)<1/1.5)

结果是1
或

x = 50:60;
y = polyval(p,x);
k = diff(y)/1;
all(abs(k)<1/1.5)

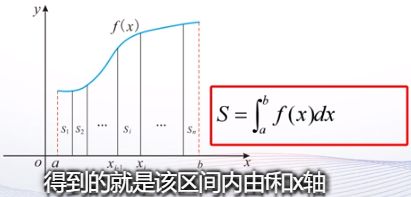
7.3 级数

7.3.1 级数求和

sum函数可以进行级数求和，但是项数必须有限，而且要表示成向量形式，如果级数是无限的或者项数非常多，用sum就无法解决了。这时，我们要用到符号表达式求和函数symsum.

%例1 求下列级数之和。
syms n;
s1=symsum(n^2,1,100)

s1 =
 	338350

s2=symsum((-1)^(n-1)/n,1,inf)

s2 =
 	log(2)

s3=symsum((-1)^(n-1)/(2*n-1),n,1,inf)

s3 =
	hypergeom([-1/2, 1], 1/2, -1) - 1 %超几何函数

hypergeom([-1/2, 1], 1/2, -1) - 1

ans =
    1.7854

eval(s3)*4  %将s3转化为数值形式再乘以4

ans =
   3.141592653589792

恰好是圆周率pi，在第三章第四节计算过这个级数，当时用的是for循环的方法，将级数的每一项计算出来依次加和，现在学习了级数加和方法之后，可以一步就计算出结果，比起用循环来，简洁多了。

%银行利率的计算问题。
syms k r;
%(1)
p2=symsum(50000*(1+0.045/k)^k,k,2,2);
eval(p2)

ans =
   5.2275e+04

%(2)
p4=symsum(50000*(1+0.045/k)^k,k,4,4);
eval(p4)

ans =
   5.2288e+04

%(3)
p12=symsum(50000*(1+0.045/k)^k,k,12,12);
eval(p12)

ans =
   5.2297e+04

%(4)
limit((1+r/k)^k,k,inf)

ans =
	exp(r)

50000*exp(0.045)

ans =
   5.2301e+04

所以即使是无数次计息，只要年利率确定，总金额也不会无限增长，它收敛于$p\ast e^r$

注意：在级数的计算中，因为小数都表示有理分数的形式，容易导致分子或分母出现极大整数从而无法计算的情况。

syms n;
s = symsum(1/n^2, n, 1, inf)

s = 
	pi^2/6

s1 = symsum(1/n^2,n,1,500)

s1 =
409896675094170203645010936925021767557940245019859473684...

eval(s1)

ans =
   NaN

7.3.2 泰勒级数

泰勒级数最重要的功能是能够将一个任意函数表示为一个幂级数，并且对于大多数工程应用问题来说，只需要取幂级数的前有限项来表示该函数就，精度已经足够了。

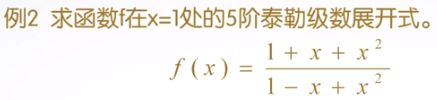
%例2 求函数f(x)在x=1处的5阶泰勒级数展开式。
syms x;
f=(1+x+x^2)/(1-x+x^2);
taylor(f,x,1,'Order',6)

ans =
	2*(x - 1)^3 - 2*(x - 1)^2 - 2*(x - 1)^5 + 3

expand(ans)  #符号变量展开函数，展开成多项式形式

ans =
 	- 2*x^5 + 10*x^4 - 18*x^3 + 12*x^2 + 1

%例3 利用泰勒展开式计算三角函数的值。
syms x;
f=taylor(cos(x),x,pi)
x=3;
eval(f)

ans =
   -0.9900

cos(3)

ans =
   -0.9900

通过泰勒级数展开的方法，成功地将三角函数的计算转换成了四则运算。

7.4 符号方程求解

7.4.1 代数方程符号求解

方法一：

syms x y a b c; 
solve(a*x^2+b*x+c==0)

方法二：

f=a*x^2+b*x+c==0;
solve(f)

方法三：

solve(a*x^2+b*x+c)

方法四：

f=a*x^2+b*x+c
solve(f)

有些时候用solve函数求解方程是会得到一个空解，而实际上这个方程是有解的，如：

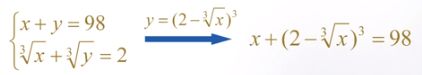
syms x y;
[u,v] = solve(x+y == 98, x^(1/3)+y^(1/3)==2)

u =
	Empty sym: 0-by-1 
v =
	Empty sym: 0-by-1

u = solve(x+(2-x^(1/3))^3 == 98)
v = 98-u

u = 
	125
v = 
	-27

7.4.2 常微分方程符号求解

syms x y t;
y=dsolve('Dy-(x^2+y^2)/x^2/2',x)

y =
                          x
 -x*(1/(C5 + log(x)/2) - 1)   %通解

常微分方程组的通解求解

[x,y]=dsolve('Dx=4*x-2*y','Dy=2*x-y',t)

x = 
	C8/2 + 2*C7*exp(3*t)
y = 
	C8 + C7*exp(3*t)

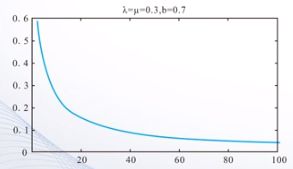
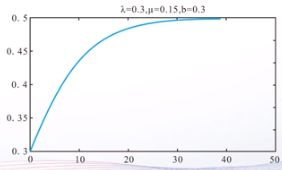
%疾病传染问题。
syms a b c y t;  % a代表λ，c代表μ，
f=dsolve('Dy=a*y*(1-y)-c*y', 'y(0)=b',t)

f = 
((a - c)*(tanh((t + (2*atanh((2*a*b)/(a - c) - 1))/(a - c))*(a/2 - c/2)) + 1))/(2*a)

假如$\lambda =\mu$，即a =c， 则再次解常微分方程：

f=dsolve('Dy=a*y*(1-y)-a*y', 'y(0)=b',t)

f = 
	1/(a*t + 1/b)