matlab笔记总结（4）

https://www.bilibili.com/video/BV1MA4y1d7so/?spm_id_from=333.788&vd_source=3ef6540f8473c7367625a53b7b77fd66

司守奎老师在B站的讲解视频

https://matlabacademy.mathworks.com/cn/details/matlab-onramp/gettingstarted
MATLAB官方的入门之旅（英文）

MATLAB软件及算法实现

1.如何调整自己的工作区
2.使用matlab时的注意事项，比如不能按CTRL+Q
3.语句后面加分号，不是交互式，不加分号，会同时打印结果 即交互式。
4.字符串使用单引号才可以。
5.变量赋值不需要提前声明，随时使用。
6.clear清除变量，clc清除屏幕。
7.who和whos查看我们已经拥有的变量的各项树形。
类型强制转换。

一、MATLAB程序设计基础

MATLAB是一款以矩阵为基本运算单位的用途广泛，发展迅速，功能强大的数学与工程计算软件，我们先从认识MATLAB软件开始。

全世界数以百万计的工程师和科学家都在使用 MATLAB® 分析和设计改变着我们的世界的系统和产品。基于矩阵的 MATLAB 语言是世界上表示计算数学最自然的方式。可以使用内置图形轻松可视化数据和深入了解数据。欢迎您使用桌面环境进行试验、探索和发现。这些 MATLAB 工具和功能全部进行了严格测试，可彼此配合工作。

MATLAB 可帮助您不仅仅将自己的创意停留在桌面。您可以对大型数据集运行分析，并扩展到集群和云。MATLAB 代码可以与其他语言集成，使您能够在 Web、企业和生产系统中部署算法和应用程序。

clear: 删除变量。
clc: 清除屏幕的内容，但是不会清除已经存在的变量。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ODpay7nJ-1682140527941)(2023-03-08-22-27-48.png)]

主界面上有5个窗口：主窗口，命令窗口，当前目录窗口，工作空间窗口，命令历史窗口，我们主要使用主窗口和命令窗口，其它窗口是辅助性的。命令窗口是我们和系统交互的场所，我们先来看一个实例：

例：计算，即123的45次方。这个问题用MATLAB来解决非常容易，只要在命令窗口中直接输入123^45，然后回车即可，得到的结果为1.1110e+094，表示。

为了进行更为复杂的运算，我们对MATLAB程序设计的一般方法作一点讨论。

1.1 MATLAB的基本操作和矩阵的基本运算

工作空间常用的管理指令有：

（1）who及whos（列出工作空间的所有变量）：查询指令

（2）clear：清除工作空间中的所有变量

 clear var1 var2：清除工作空间中的变量var1和var2 
 clc: 清理窗口

（3）save FileName ：把全部内存变量保存为Filename.mat文件

 save FileName v1 v2：把变量v1和v2保存为Filename.mat文件
 save FileName v1 v2 –append：把变量v1和v2添加到Filename.mat文件

（4）load FileName ：把Filename.mat文件中全部变量调入内存
load FileName v1 v2：把Filename.mat文件中v1 , v2调入内存

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aFS9IXeJ-1682140527943)(2023-04-10-19-32-10.png)]

连接字符串
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jr9cj2kr-1682140527944)(2023-04-10-19-38-02.png)]

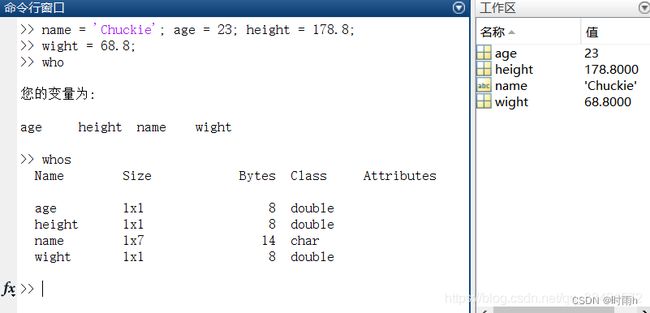
who whos
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jkZwgK29-1682140527945)(2023-04-10-19-48-59.png)]
（如果我们在一行中以 ; 分割，那么每个单独语句会被单独执行）

上面的栗子中，我们可以清楚地看到who 和 whos 的区别，who这个命令仅仅是列出变量的名字，而whos这个命令，显示的信息更加的全面，包括数据的大小（由于matlab默认用二维数组存放，所以对于数字，就是一行一列的数组，就是单个的值），类型，占了多少空间等数据。

baseNum = 123.456;
toUint8 = uint8(baseNum);
toUint32 = uint32(baseNum);%这个是注释的符号%
whos;

​

​​桌面基础知识

启动 MATLAB® 时，桌面会以默认布局显示。

桌面包括下列面板：


使用 MATLAB 时，可发出创建变量和调用函数的命令。例如，通过在命令行中键入以下语句来创建名为 a 的变量：

a = 1
MATLAB 将变量 a 添加到工作区，并在命令行窗口中显示结果。

a = 1
创建更多变量。

b = 2
b = 2
c = a + b
c = 3
d = cos(a)
d = 0.5403

如果未指定输出变量，MATLAB 将使用变量 ans（answer 的缩略形式）来存储计算结果。

sin(a)
ans =0.8415

如果语句以分号结束，MATLAB 会执行计算，但不在命令行窗口中显示输出。

e = a*b;
按向上 (↑) 和向下箭头键 (↓) 可以重新调用以前的命令。在空白命令行中或在键入命令的前几个字符之后按箭头键。例如，要重新调用命令 b = 2，请键入 b，然后按向上箭头键。

​

2.矩阵的产生

MATLAB的操作对象为矩阵。标量被看作是1×1的矩阵，维行向量或列向量可看作是或维矩阵。
行向量生成基本格式：start: step: end（step缺省时为1）
例如：在命令窗口中提示符>> 后输入，x=1:5，按回车【Enter】后，显示输出结果如下：

x =
1 2 3 4 5

Matlab的每条命令后，若为逗号“，”或无标点符号，则显示命令的结果；若命令后为分号“；”，则禁止显示结果，用“%”来实现注释功能。

利用下面两个函数也可以产生向量。

linspace：线性等分向量，例如，a=linspace(0,2*pi,100)。

logspace：对数等分向量，例如，a=logspace(0,2*pi,100)。

在矩阵的输入中，约定：(1) 元素之间用空格或逗号隔开；

(2) 用中括号方[ ]把所有元素括起来；

(3) 用分号（；）说明行结束。
在命令窗口，输入矩阵时，按Shift+Enter键表示开始输入新的一行，且要求所有的行具有相同的列。
例如：a=[1 2 3; 4,5 6; 7 8,9]
该矩阵一直保存在工作空间，直至被修改。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U90y57Sh-1682140527947)(2023-04-10-20-12-42.png)]

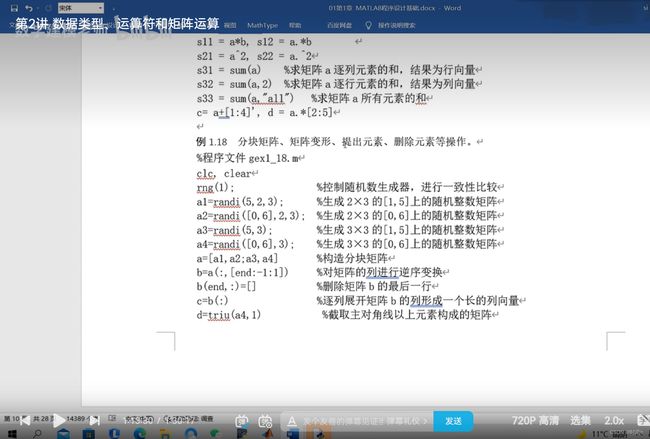
%程序文件gex118.m
clc,cleare
8(1);
%控制随机数生成器，进行一致性比较
al=and(5,2,3):
%生成2×3的[1,5]上的随机整数矩阵
a2=xand([0,6],2,3);
%生成2×3的[0,6]上的随机整数矩阵
a3-randi(5,3);
%生成3×3的[1,5]上的随机整数矩阵
a4=xand([0,6],3);
%生成3×3的[0,6]上的随机整数矩阵
a=[al,a2;a3,a4]
%构造分块矩阵
b=a(:,[end:-1:l])
%对矩阵的列进行逆序变换
b(end,:)=[]
%删除矩阵b的最后一行
c=b(:）
%逐列展开矩阵b的列形成一个长的列向量~
d=triu(a4,1)
%截取主对角线以上元素构成的矩阵

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tczup5JP-1682140527948)(2023-04-10-20-14-10.png)]

MATLAB画图

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2SRHVUvG-1682140527948)(2023-04-21-16-52-43.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jAFxF3nk-1682140527948)(2023-04-21-16-56-30.png)]

二维图和三维图

线图
要创建二维线图，请使用 plot 函数。例如，绘制在从 0 到 2π 的值组成的线性间距向量上的正弦函数：

x = linspace(0,2*pi);
y = sin(x);
plot(x,y)


可以标记轴并添加标题。

xlabel("x")
ylabel("sin(x)")
title("Plot of the Sine Function")


通过向 plot 函数添加第三个输入参数，您可以使用红色虚线绘制相同的变量。

plot(x,y,"r--")


"r--" 为线条设定。每个设定可包含表示线条颜色、样式和标记的字符。标记是在绘制的每个数据点上显示的符号，例如，+、o 或 *。例如，g:*" 请求绘制使用 * 标记的绿色点线。

请注意，为第一幅绘图定义的标题和标签不再被用于当前的图窗窗口中。默认情况下，每次调用绘图函数、重置坐标区及其他元素以准备新绘图时，MATLAB® 都会清空图窗。

要将绘图添加到现有图窗中，请使用 hold on。在使用 hold off 或关闭窗口之前，当前图窗窗口中会显示所有绘图。

x = linspace(0,2*pi);
y = sin(x);
plot(x,y)

hold on

y2 = cos(x);
plot(x,y2,":")
legend("sin","cos")

hold off


三维绘图
三维图通常显示一个由带两个变量的函数 z=f(x,y) 定义的曲面图。例如，对于给定的行向量和列向量 x 和 y，每个向量包含 [-2,2] 范围内的 20 个点，计算 z=xe
−x
2
−y
2
 。

x = linspace(-2,2,20);
y = x';
z = x .* exp(-x.^2 - y.^2);
然后，创建曲面图。

surf(x,y,z)


surf 函数及其伴随函数 mesh 以三维形式显示曲面图。surf 使用颜色显示曲面图的连接线和面。mesh 生成仅以颜色标记连接线条的线框曲面图。

多个绘图
您可以使用 tiledlayout 或 subplot 在同一窗口的不同部分显示多个绘图。

tiledlayout 函数是在 R2019b 中引入的，该函数比 subplot 提供更多对标签和间距的控制。例如，在图窗窗口中创建 2×2 布局。然后，每当您要某个绘图出现在下一区域中时，请调用 nexttile。

t = tiledlayout(2,2);
title(t,"Trigonometric Functions")
x = linspace(0,30);

nexttile
plot(x,sin(x))
title("Sine")

nexttile
plot(x,cos(x))
title("Cosine")

nexttile
plot(x,tan(x))
title("Tangent")

nexttile
plot(x,sec(x))
title("Secant")

计算一元二次方程

以科学计算开始，使用matlab计算精确度很高，我们可以尝试来计算一下黄金分割率（定义大家可以自行百度一下，这里就不再说了）：

计算黄金分割率的公式是：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0i7Biv3O-1682140527949)(2023-04-22-11-39-06.png)]

如果使用加法，得到的是1.618…，如果使用减法，得到的是0.618…，这两个结果都是正确的。因为他们两个只相差1.

首先，我们把这个公式转化一下，把根号去掉，转化为一个一元二次方程：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AnqftjgQ-1682140527949)(2023-04-22-11-39-24.png)]

（因为+号时无解，所以舍去）

然后我们就只需要使用matlab解开这个方程了！

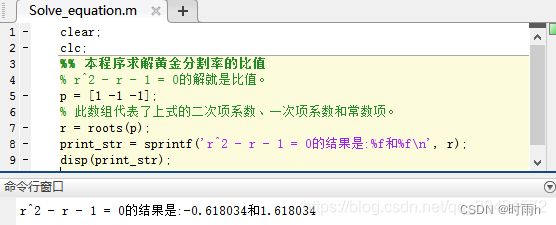
clear;
clc;
%% 本程序求解黄金分割率的比值
% r^2 - r - 1 = 0的解就是比值。
p = [1 -1 -1];
% 此数组代表了上式的二次项系数、一次项系数和常数项。
r = roots(p);
print_str = sprintf('r^2 - r - 1 = 0的结果是:%f和%f\n', r);
disp(print_str);

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ziBTm98n-1682140527949)(2023-04-22-11-39-37.png)]
当然，如果我们实现不知道各个系数，只知道我们的公式（假设），我们可以使用solve函数来计算，可以大大节省我们的时间：

%% 第二种计算的方法。
clear;
clc;
r2 = solve('r^2 - r - 1 = 0');
print_str = sprintf('r*r - r - 1 = 0的结果是:%f和%f\n', r2);
disp(print_str);

同样也能得到我们想要的结果，但同时注意：占位符是 %f 千万不能写成其他的。

但是你可能觉得这个精确度不高，没问题，使用 vpa 方法可以提高精确度到很多位！！

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nVyeDkvD-1682140527949)(2023-04-22-11-41-28.png)]

第一个参数是我们的数据，第二个参数是我们精确到小数点后的位数。可以得到很多位的结果（好像理论是无限，但是前提是电脑的CPU够厉害并且你有足够的耐心并且你的内存够大！！在我的电脑上，计算到小数点后五万位已经有明显的一秒左右延迟了。）

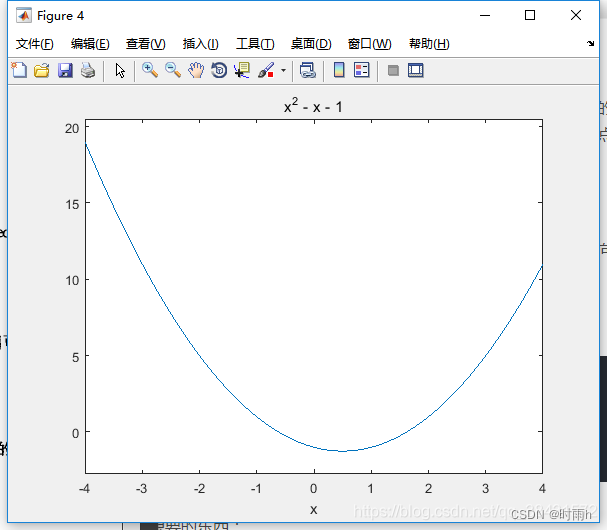
看一元方程的图形

上面我们计算了这个方程，大家知道，在数学中，一元二次方程的表现是开口向上或者向下的抛物线，方程的解就是与X轴的交点（即零点）。

那么如何在matlab中表现呢？下面上代码！

%% 显示函数的图像

f = inline( 'x^2 - x - 1');  % 写出我们的函数
% 但是这个inline马上就不能用了，但是只是前期学习，不要介意
ezplot(f, -4, 4);   %显示我们的函数图形，
hold on;

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uNsv9ZsL-1682140527950)(2023-04-22-11-42-24.png)]

有个小疑问？

假如我们写成另一个形式呢（1/x - (x - 1)）？很容易知道，这俩图像虽然图形不一样，但是也是黄金分割率公式的变形，只需移项消元即可得到这个形式，很明显，这个世子有个点是不存在的（点0，不能为分母），这个公式的图形也明显类似于反比例函数（在点0处的间断点是第二类间断点，0+0处是正无穷大，0-0处是负无穷大）。

这个没问题！matlab会计算我们需要的函数图形，有间断点会计算极限，尽可能的满足我们（这次我们在代码里标出这个解的位置），代码如下：

%% 第二种形式
f = inline('1/x - (x - 1)');  % 写出我们的函数
ezplot(f, -2, 2);
zeor1 = fzero(f, 1);  % 找第一个函数零点，在x=1附近
zero2 = fzero(f, -1); % 找第二个函数零点，在x=-1附近
hold on;
plot(zeor1, 0, 'o'); % 在第一个零点出画一个字母o
plot(zero2, 0, 'o'); % 在第一个零点出画一个字母o
而图形，如同我们预期，显示出了一个双曲线，并且在零点处标出了我们的符号：
————————————————
版权声明：本文为CSDN博主「ChuckieZhu」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_38431572/article/details/105127864

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mtolQoWL-1682140527950)(2023-04-22-11-42-55.png)]

使用roots函数求一元二次方程的根。

使用solve函数求方程的根（注意哦，没说是几次的。大家可以试试三次函数等，甚至没实数根的大家也可以试试，我们要从认识得到实践，然后再根据实践得到新的认识！）

使用inline函数和ezplot函数一起绘制函数图形（小技巧：ezplot音似：easy plot，简单绘制，方便我们记忆）

使用 fzero 函数和 plot 函数绘制某一点处的零点。

斐波那契数列——新手来看，保证看懂。

https://blog.csdn.net/qq_38431572/article/details/105207508
编写 fibo_use.m 文件的内容代码

%% 清理可能存在的旧数据
clc; % 清屏
clear;  % 清除变量
close;  % 关闭可能存在的窗口
%% 我们在这里调用，这里是主要代码
n = 5; % 我们计算前几个斐波那契数列
res = fibonacci_mine(n);  % 调用计算函数
disp('结果是：')
disp(res);  % 打印结果

编写 fibonacci_mine.m 文件中的代码

function fibo = fibonacci_mine(n)
% 功能：计算前n个斐波那契数列
% 参数：n 代表需要前n个斐波那契数列
% 返回值： fibo  一个 n行1列的矩阵，代表前n个斐波那契数
fibo = zeros(n, 1);  % 把fibo作为n行1列的空矩阵，里面元素都为0
fibo(1) = 1;  
fibo(2) = 2;  % 把启动条件写出来
for k = 3:n  % for 循环，从 3 到 n（包含 3 也包含 n）
    fibo(k) = fibo(k-1) + fibo(k-2);
end
return 

今日总结

今天，我们通过计算斐波那契数列，学到了下面的知识点：

如何声明、定义、调用函数（文件）。

给函数传递参数、接受函数的返回值。

matlab中矩阵的简单使用和下标索引。

一句话：我调用你，与你无关。即软件工程的思想：模块化。

matlab中for循环（遍历）的使用。

如何从一个文件调用另一个函数文件。

使用matlab求解线性方程组

https://blog.csdn.net/qq_38431572/article/details/105585584

非常详细+补充基本知识
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9JdoVUWg-1682140527950)(2023-04-22-11-58-07.png)]

%% 显示这两个矩阵
%% 方程组求解
clc;
clear;
A = [4 1 -2;
     2 2  1;
     3 1 -1];
% 定义一个3行3列的矩阵A，行与行之间使用分号隔开，每一行之间的元素使用空格隔开
B = [1;
     2; 
     3]; %定义矩阵B
disp(A);disp(B); %显示A和B
X = A\B;  % 左除
disp(X);

可能会有些人觉得奇怪，怎么A在左边并且这个写的是斜杠呢？

如果我们学习过矩阵便知道，矩阵的乘法是没法前后调换的，即 AB 不等于 BA，也就是说，AX = B，要求这个X，我们需要在两边的左边同时除以A（严谨说法叫做乘以A的逆矩阵），即 1/A * A X = 1/A * B，也叫做左除，而在matlab中，左除符号就是这个“ \ ”符号，所以应这样使用，**即 A \ B代表 1/A * B（**严谨来说，就是A的逆矩阵B），即可得到X。

运行后我们便可看到解矩阵的结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QChYPvew-1682140527951)(2023-04-22-12-04-14.png)]

左除和右除

https://blog.csdn.net/qq_38431572/article/details/105585584

零基础学线代 ｜ 矩阵的乘法（左乘与右乘，可交换矩阵）
https://www.bilibili.com/video/BV1QP4y1d71i/?spm_id_from=333.337.search-card.all.click&vd_source=3ef6540f8473c7367625a53b7b77fd66

更好的来处理矩阵的乘法运算

然后根据乘法的运算法则，可以发现，这个方程是没法解的（因为根本就没法乘，前面矩阵1列，后面矩阵3行，不相等，没法进行乘法运算）
所以，如果进行这样的乘法运算，我们需要把X的解矩阵变换（注意，变换后乘出来的结果和之前的方程组不一样，不一样！）：

总结

在matlab中定义矩阵：A = [1 2 3; 2 3 4; 3 4 5]，每行元素空格隔开，两行之间使用分号隔开。

线性代数矩阵乘法运算、求解知识。乘法时注意行列的数量，要前列=后行才能相乘。且AB不一定等于BA（还是有可能相等的，所以用不一定）

关于矩阵乘法左除、右除的区别。AX=B，求X用左除，XA=B，求X用右除。

在matlab中求解两种矩阵方程的方法。X=A\B（左除斜线向左），X=B/A（右除斜线向右）。

使用matlab求解定积分和不定积分的问题

https://blog.csdn.net/qq_38431572/article/details/105822907

计算不定积分

%%计算不定积分
clc; clear;
syms x;  % 定义一个符号，x。
f = 'x';  % 定义一个原函数
F = int(f, x);  % 计算不定积分
disp(F); % 显示原函数

没错，就是这个int函数即可，下面逐句讲解代码：

syms x; 定义一个符号x，代表我们函数中的变量的名字，比如：y = 2x中的x就是变量。

f = ‘x’; 这句话就是声明了个字符串，没什么特别之处。

F = int(f, x); int函数是计算积分的函数，第一个参数是函数字符串，第二个参数是变量的符号

如果我们定义的符号是t，即(syms t;)，我们下面就需要写f = ‘t’，F = int(f, t)。。。。。

int函数将计算结果以字符串形式返回，我们用一个变量接收，同时disp显示到屏幕上，我们就能看到输出的结果：

很容易验证，x的一个原函数就是x^2/2。（这个int函数只返回一个原函数，如果需要其他的自行加上常数即可）。

在matlab中计算定积分

计算定积分时，和不定积分一样简单，代码只需改动少量即可：

%%计算定积分
clc; clear;
syms x;  % 定义一个符号，x。
f = 'x';  % 定义一个原函数
F = int(f, x, 0, 10);  % 计算不定积分
disp(F); % 显示原函数

与计算不定积分唯一的区别就是函数不同，在定积分中，int的参数列表是这样的：

1. 函数

2. 变量符号

3. 下限

4. 上限

使用matlab建立多项式以及求导，商求导乘积求导等

使用matlab建立多项式

clc;clear;
%% 使用matlab建立多项式
p = [4 3 2 1 1]; %确定各项系数，和常数项。放在一个数组里面。
y = poly2sym(p); %创建目标多项式，这个函数返回了一个符号变量，即我们的函数
disp(y); %显示y.

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N7B0Vm9r-1682140527952)(2023-04-22-12-42-29.png)]

PS: 如果需要定义一个特殊的函数比如 y = 4x^4 ，那么我们可以认为3次、2次、1次系数都为0，常数项也为0，写入数组即可。

通过已知方程的根建立多项式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uohtGvHN-1682140527953)(2023-04-22-12-42-41.png)]

clc;clear;
%% 使用根建立多项式
r = [1 2 3]; %随意编一些根
p = poly(r); %调用求多项式的函数
y = poly2sym(p); %得到多项式的符号变量
disp(y);

对多项式进行求导

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CToZTQOg-1682140527954)(2023-04-22-12-44-34.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pSAz7LMx-1682140527955)(2023-04-22-12-44-47.png)]

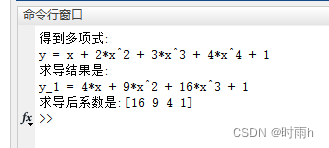
使用matlab进行求导

clc; clear;
%% 对多项式进行求导
p = [4 3 2 1 1]; %建立我们的多项式
y = poly2sym(p); %得到多项式的符号变量
temp_str = sprintf('得到多项式:\ny = %s', y); %将式子格式化到一个字符串中
disp(temp_str); %显示
p_1 = polyder(p); %求一次导,注意polyder求导传递的是p而不是y
y_1 = poly2sym(p_1); %转化为符号变量
temp_str = sprintf('求导结果是:\ny_1 = %s\n求导后系数是:[%d %d %d %d]', y_1, p_1);
disp(temp_str);

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fGReLCwM-1682140527955)(2023-04-22-12-45-37.png)]

y_1中的常数1来自于y中的x求导，y中的1求导后成为了0，就没了。

那么，这仅仅是一个多项式求导，乘积求导、商求导，请继续往下看：

%% 乘积求导
clc; clear;
p_1 = [4 4 2];
p_2 = [2 4 5]; % 随意胡诌几个数
y_1 = poly2sym(p_1);
y_2 = poly2sym(p_2); % 转化为符号变量
temp_str = sprintf('原来的两个函数为：\n 1. y_1 = %s\n 2. y_2 = %s', y_1, y_2);
disp(temp_str);
res_p = polyder(p_1, p_2); % 乘积求导后的系数
res_y = poly2sym(res_p); %转化为符号变量
temp_str = sprintf('结果为：y = %s', res_y);
disp(temp_str);

商求导：

这个部分比较麻烦，商求导后返回值是有两个，因为很有可能出现求导后还是分数的形式，所以返回值是一个分子、一个分母，代码如下：

%% 商求导
clc; clear;
p_1 = [4 4 2];
p_2 = [2 4 5]; % 随意胡诌几个数
y_1 = poly2sym(p_1);
y_2 = poly2sym(p_2); % 转化为符号变量
temp_str = sprintf('原来的两个函数为：\n 1. y_1 = %s\n 2. y_2 = %s', y_1, y_2);
disp(temp_str);
[res_p_Num, res_p_Den] = polyder(p_1, p_2);
% 注意此处，与乘积求导几乎一样，只是返回值不同，
% 前面的是分子，后面的是分母
res_y_Num = poly2sym(res_p_Num);
res_y_Den = poly2sym(res_p_Den); %转化为符号变量
temp_str = sprintf('结果为：y = (%s)/(%s)', res_y_Num, res_y_Den);
disp(temp_str);

————————————————
版权声明：本文为CSDN博主「ChuckieZhu」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_38431572/article/details/106591517

商求导分子分母为什么要分开获得???

polyder函数的定义就是这样

[q,d]=polyder(a,b)

q代表求导后分子多项式的系数矩阵，d代表分母多项式的系数矩阵

高级积分运算、二重积分

复习定积分（单变量）
在之前，先复习一下之前学习的内容。使用matlab求解定积分的步骤大概如下：

定义符号变量（syms关键字）

定义内联函数（inline函数）

使用matlab内置函数进行计算定积分或者不定积分（使用int函数，具体求解定积分还是不定积分，根据参数的数量决定）
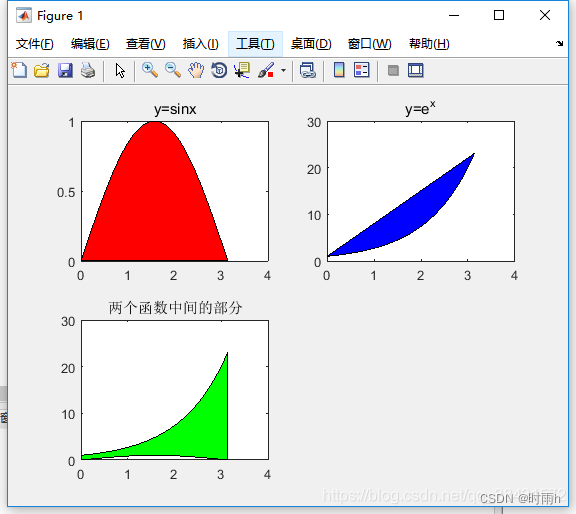
我们都知道：定积分是求解一个图形与坐标轴围成的面积。而今天我们需要深入理解一下：定积分是求解两条曲线之间围成的面积，如果只有一个公式，比如x，我们可以理解成 x-0，y=x 这个函数减去了 y=0这个常数函数，或者说，上面函数与x轴围成的面积减去了下面函数与x轴围成的面积（并且这个面积在x轴上方是正的，下方是负的），这样我们就可以推广，假设我们现在有两条曲线，一个是sinx，一个是 ,我们求在0-pi的范围内，两个图形围成的面积，容易知道，两个图形大概是这样围起来的：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GLJ05t8q-1682140527956)(2023-04-22-12-49-22.png)]

%% 目标图像
clc;clear all;  % 清除原先的东西
 
x = 0:0.01:pi;  % x的范围是0-pi，以0.01为一个小分割点细分出一个范围
y1 = sin(x);    % sinx
y2 = exp(x);    % e^x
 
figure;         % 弄一个figure的框体
hold on;        % 保持这个窗体，保证后面的内容都画在了上面，hold off解除
 
subplot(221);   % 开辟子窗体，221:共2行2列，里面的第一个
fill(x,y1,'r'); % 画图并填充颜色，变量是x，函数是y1，颜色是r，红色
title('y=sinx');% 设置标题，必需先fill，才能添加标题，否则会失败
 
subplot(222);   % 开辟子窗体，222，共2行2列，里面第二个
fill(x,y2,'b'); % b 蓝色
title('y=e^x');
 
subplot(223);   % 开辟子窗体，223，共2行2列，里面第三个
fill([x, fliplr(x)],[y1,fliplr(y2)],'g');
                % 两个函数直接填充颜色，每一个方括号代表一个函数的内容
title('两个函数中间的部分');
hold off;

%% 对上面的函数进行计算定积分
syms x;
f = 'exp(x) - sin(x)';
res_int = int(f, x, 0, pi);
disp(res_int);

二重积分

https://blog.csdn.net/qq_38431572/article/details/107008015

%% 计算二重积分
clear all;
f = @(x,y)x.*cos(y); % 定义一个函数句柄，两个变量分别是x,y
% 这样定义函数句柄时，需要在所有的运算前加一个.（表示对应元素各自计算，不按照矩阵的规则）
ymax = @(x) x;  % 根据0<=y<=x处，右方的y=x反解出y，
res = integral2(f,0,1,0,ymax);
% 计算二重积分的函数 
% integral2(fun, xmin, xmax, ymin, ymax)
disp(res);

%% 看一看这个曲面吧
[x,y] = meshgrid(0:0.001:1, 0:0.001:1);
% 设置x和y的区间，以及细分程度
z = (x.*cos(y));  % 使用一个z来代表这个函数
mesh(x,y,z)  % 画出二维曲面图像
title('x*cos(y)')

二维中的数据可视化，使用matlab绘图

https://blog.csdn.net/qq_38431572/article/details/107289661

MATLAB数据可视化

绘图

绘制图形（二维）一般使用plot函数，这个函数一般能满足很多画图的功能了，比如我们能绘制一个函数图像：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vOT9vqTo-1682140527957)(2023-04-22-12-56-07.png)]

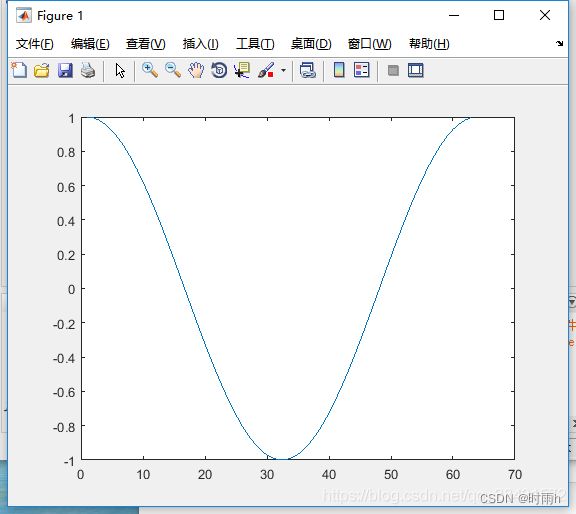
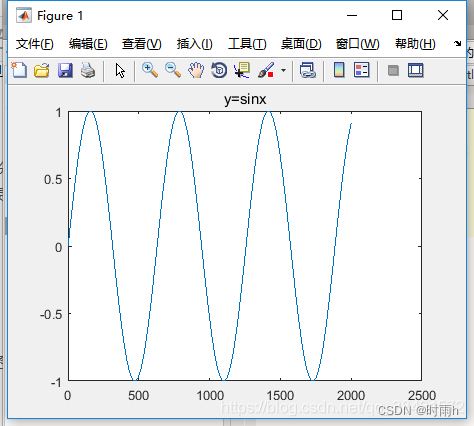
%% 使用plot绘图
clear all;
syms x;     % 声明一个符号x
x = 0:0.01:20;  % 给定范围
f = sin(x);   % 声明函数
figure;     % 打开绘图窗口
plot(f);    % 画图
title('y=sinx');

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TmN6zofH-1682140527957)(2023-04-22-13-02-56.png)]

%% 使用plot绘图
clear all;
syms x;     % 声明一个符号x
x = 0:0.01:20;  % 给定范围
f = sin(x);   % 声明函数
figure;     % 打开绘图窗口
plot(f,'o--c');    % 画图
title('y=sinx o--c');

在同一个figure里面绘制多个图形

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jILR62Dg-1682140527958)(2023-04-22-13-03-41.png)]

%% 同时绘制多个函数在一起
clear all;
syms x;
x = 0:0.01:pi/3;  % 设置x的取值范围
% f = [sin(x);
%    tan(x);
%    x];  % 定义一个函数的矩阵
f = [sin(x);tan(x);x];
figure;
plot(x, f);

本期小结

相比于前几期的内容，本期内容似乎有点轻松，但是我感觉也算是讲清楚了plot的用法（至少现阶段绝对是够用了，并且能准确的理解里面的内容），下面来小结一下吧：

学会了使用plot绘制一个向量

学会了使用plot绘制一个函数图像

学会了使用plot绘制一个矩阵的折线图

学会了绘制多个函数在同一个图像中

懂得了x 和函数 f 的实质内容

学会了定制绘图的曲线样式。

二维中的数据可视化，使用matlab绘图

https://blog.csdn.net/qq_38431572/article/details/113127864

画一个图像并且给图像加上标题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s4sldssz-1682140527958)(2023-04-22-13-06-47.png)]

%% 给图形加上标题（这个我记得前面提过）
syms x;     % 声明一个变量x
x = 0:0.1:2*pi;   % x的取值范围，从0-2*pi，以0.1为分割取值
y = cos(x);         % 函数
figure;     % 打开绘图窗口
plot(y);     % 画出y，如果你想更改曲线形状，可以参考第九讲，比如
            % plot(y, 'o--c')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TU8VRGHR-1682140527959)(2023-04-22-13-07-12.png)]

三维中的数据可视化

https://blog.csdn.net/qq_38431572/article/details/113524903

三维中有plot()吗？
在三维画图中，有对应的 plot3() 函数用于画三维空间中的图像，但是，我们回忆一下plot是如何工作的：

plot接收的参数是矩阵（或者说数组），然后根据传入的参数画点，使用直线把点连接起来，如果点足够密集，展示出来后，在我们眼睛看来，画出来就是一个曲线。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BFOakdyz-1682140527959)(2023-04-22-13-11-31.png)]

%% plot对比
x1 = 0:0.1:2*pi;    % x1 每两个点的距离是0.1
y = sin(x1);
x2 = 0:1:2*pi;      % x2 每两个点的距离是1
z = sin(x2);
figure;
subplot(2, 1, 1);   % 分块画图
plot(x1, y);        % 画sinx1
title('密集打点 y=sinx1')
subplot(2, 1, 2);
plot(x2, z);        % 画sinx2
title('不太密集打点 z=sinx2');

而 plot3() 同样，也是在传入的三个矩阵中找三维空间中的点，然后使用直线连接，所以可以很直观的理解到：plot3() 是画的空间曲线（直线）。我们下面看个例子：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iSYUAwWF-1682140527961)(2023-04-22-13-11-55.png)]

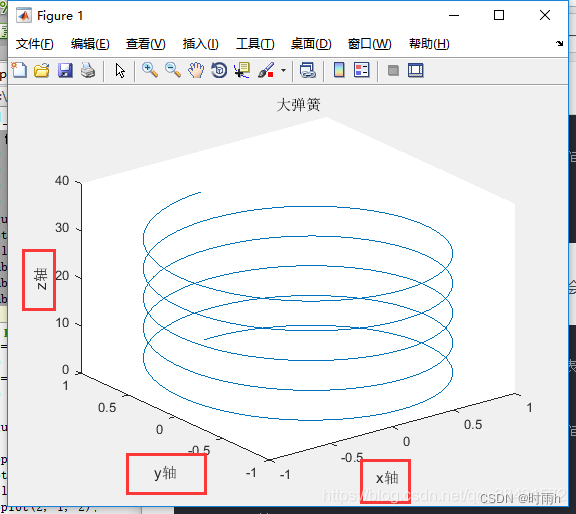
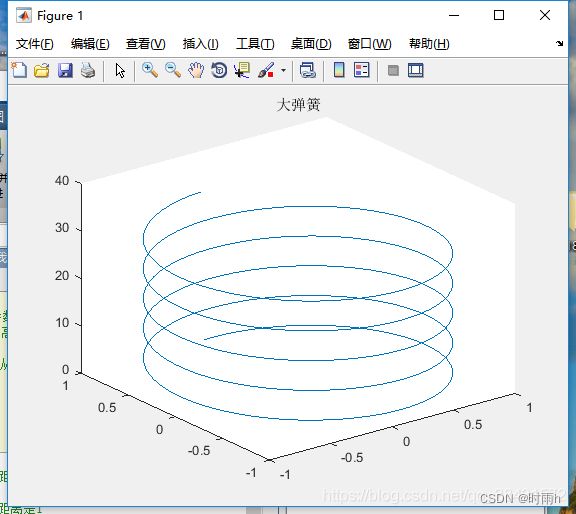
%% 使用plot3 画一个螺旋向上的线
t = 0:0.1:10*pi;    % 空间曲线使用参数方程比较容易表示出来
z = t;          % z轴随着t的增加而升高
x = sin(t);
y = cos(t);     % x^2+y^2 = 1，所以从上向下看是空间圆
figure;
plot3(x, y, z); % 画图
title('大弹簧');

其余的参数和二维中的plot 大同小异，相信大家都能会了，这里还有一个小知识点，补充一下：如果我们想给坐标轴命名，使用下面的代码：

%% 使用plot3 画一个螺旋向上的线
t = 0:0.1:10*pi;    % 空间曲线使用参数方程比较容易表示出来
z = t;          % z轴随着t的增加而升高
x = sin(t);
y = cos(t);     % x^2+y^2 = 1，所以从上向下看是空间圆
figure;
plot3(x, y, z); % 画图
title('大弹簧');
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')

在二维中，不写zlabel即可，如图：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uHSZm82h-1682140527961)(2023-04-22-13-12-35.png)]

我想画曲面，怎么画？
在第八讲中我们稍微提了一下meshgrid()和mesh()画出一个空间曲面，我们先来回顾一下这两个函数（假设我们画z = sinx + cosx吧，随便捏造的函数）：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WaNRIuQt-1682140527962)(2023-04-22-13-12-48.png)]

%% meshgrid和mesh的使用
clear all;
[x, y] = meshgrid(-2*pi:0.1:2*pi, -2*pi:0.1:2*pi);
z = sin(x) + cos(x);
figure;
mesh(x, y, z);
title('z = sinx + cosx');