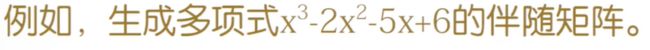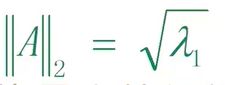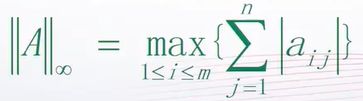MATLAB笔记2:MATLAB矩阵处理
目录
一、特殊矩阵
1.zeros函数的调用格式
2.用于专门学科的特殊矩阵
魔方矩阵 Magic Square
范德蒙矩阵
希尔伯特矩阵
伴随矩阵
帕斯卡矩阵
二、矩阵变换
1.对角阵
提取矩阵的对角线元素
构造对角矩阵
2.三角阵
上三角阵
下三角阵
3.矩阵的转置
4.矩阵的旋转
5.矩阵的翻转
6.矩阵的求逆
三、矩阵求值
1.方阵的行列式
2.矩阵的秩
3.矩阵的迹
4.向量和矩阵的范数
向量的三种常用范数:
矩阵的范数
5.矩阵的条件数
四、矩阵的特征值与特征向量
1.矩阵特征值的数学定义
2.特征值的集合意义
五、稀疏矩阵
1.矩阵的存储方式
2.稀疏存储方式的产生
完全存储方式与稀疏存储方式之间的转化
直接建立稀疏存储矩阵
带状稀疏矩阵得稀疏存储
单位矩阵的稀疏存储
一、特殊矩阵
zeros函数:产生全0矩阵,即零矩阵。
ones函数:产生全1矩阵,即幺矩阵。
eye函数:产生对角线为1的矩阵。当矩阵是方阵时,得到一个单位矩阵。
rand函数:产生(0,1)区间均匀分布的随机矩阵。
randn函数:产生均值为0,方差为1的标准正态分布随机矩阵。
1.zeros函数的调用格式
zeros(m):产生m*m零矩阵。
zeros(m,n):产生m*n零矩阵。
zeros(size(A)):产生与矩阵A同样大小的零矩阵。
其中,size函数返回矩阵A的行数列数组成的向量
例子:
>> A=zeros(2,3)
A =
0 0 0
0 0 0
>> zeros(size(reshape(A,3,2)))
ans =
0 0
0 0
0 0
其中,
reshape函数将A转换为3行2列的函数。
例子:
首先产生5阶两位随机整数矩阵A,再产生均值为0.6、方差为0.1的5阶正态分布随机矩阵B,最后验证(A+B)L = LA+LB(其中L为单位矩阵)。
rand函数:产生(0,1)开区间均匀分布的随机数x。
fix(a+(b - a + 1)*x):产生[a,b]区间上均匀分布的随机整数。
randn函数:产生均值为0、方差为1的标准正态分布随机数x。
u + 西格玛x:得到均值为u,方差为西格玛的平方的随机数。
double是MATLAB中默认数值数据类型,它可为大多数计算提供足够的精度。数值变量自动存储为64位(8字节)双精度浮点值。
>> A=fix(10+(99-10+1)*rand(5));
>> B=0.6+sqrt(0.1)*randn(5);
>> C=eye(5);
>> (A+B)*C==C*A+B*C
ans =
5×5 logical 数组
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1其中,sqrt,平方根。
logical 将数值转换未逻辑值。
语法:L=logical(A) 将 A 转换为一个逻辑值数组。A 中的任意非零元素都将转换为逻辑值 1 (true),零则转换为逻辑值 0 (false)。复数值和 NaN 不能转换为逻辑值,因此会导致转换错误。
2.用于专门学科的特殊矩阵
魔方矩阵 Magic Square
>> M=magic(3)
M =
8 1 6
3 5 7
4 9 2n阶魔方阵由1、2、3、... 、n方共n方个整数组成,且每行、每列以及主、副对角线上各n个元素之和都相等。
n阶魔方阵每行每列元素的和为(1+2+3+...+n方)/n = (n + n三次方)/2。
MATLAB函数magic(n)产生一个特定的魔方阵。
例子:产生8阶魔方阵,求其每行每列元素的和。
>> M=magic(8);
>> sum(M(1,:))
ans =
260
>> sum(M(:,1))
ans =
260范德蒙矩阵
在MATLAB中,函数vander(V)生成以向量V为基础的范德蒙(Vandermonde)矩阵。
>> A=vander(1:5)
A =
1 1 1 1 1
16 8 4 2 1
81 27 9 3 1
256 64 16 4 1
625 125 25 5 1
范德蒙矩阵常用在各种通信系统的纠错编码中,例如,常用的Reed-Solomon编码即以范德蒙矩阵为基础。
希尔伯特矩阵
在MATLAB中,生成n阶希尔伯特矩阵的函数时hilb(n)
>> format rat
>> H=hilb(4)
H =
1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6 其中,rat为转换成有理数的形式输出,有理分式近似值
伴随矩阵
MATLAB生成伴随矩阵的函数是compan(p),其中p是一个多项式的系数向量,高次幂系数排在前,低次幂系数排在后面。
>> p=[1,-2,-5,6];
>> A=compan(p)
A =
2 5 -6
1 0 0
0 1 0 伴随矩阵特征值的根等于多项式的根
帕斯卡矩阵
杨辉三角形表是二项式 (x+y)^n 展开后的系数随自然数 n 的增大组成的一个三角形表。
如4阶帕斯卡矩阵为:
Pascal(4)=
[1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20]
对比杨辉三角:
以上即为杨辉三角的排列性质
pascal是矩阵实验室(Matrix Laboratory)MATLAB中的函数,利用pascal函数可以在矩阵实验室中方便的得到任意阶帕斯卡矩阵。设A为帕斯卡矩阵,则在MATLAB命令窗口中输入A=pascal(n),n为正整数,可得到阶数为n的帕斯卡矩阵。
Pascal矩阵的第一行元素和第一列元素都为1,其余位置处的元素是该元素的左边元素加上同列中行数小于其的其他元素。例如:a(i,j)=a(i,j-1)+a(i-1,j-1)+……+a(1,j-1)。
>> format rat
>> P=pascal(5)
P =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> inv(P)
ans =
5 -10 10 -5 1
-10 30 -35 19 -4
10 -35 46 -27 6
-5 19 -27 17 -4
1 -4 6 -4 1
二、矩阵变换
包括
对角阵
三角阵
矩阵的转置
矩阵的旋转
矩阵的翻转
矩阵求逆
1.对角阵
对角矩阵:只有对角线上有非零元素的矩阵。
数量矩阵:对角线上的元素相等的对角矩阵。
单位矩阵,对角线上的元素都为1的对角矩阵。
提取矩阵的对角线元素
diag(A):提取矩阵A主对角线元素,产生一个列向量。
diag(A,k):提取矩阵A第k条对角线的元素,产生一个列向量。
构造对角矩阵
diag(V):以向量V为主对角线元素,产生对角矩阵。
diag(V,k):以向量V为第k条对角线元素,产生对角矩阵。
例子:
先建立5*5矩阵A,然后将A的第一行元素乘以1,第二行乘以2,... ,第五行乘以5。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]
A =
7 0 1 0 5
3 5 7 4 1
4 0 3 0 2
1 1 9 2 3
1 8 5 2 9
>> D=diag(1:5);
>> D*A
ans =
7 0 1 0 5
6 10 14 8 2
12 0 9 0 6
4 4 36 8 12
5 40 25 10 45
例子:要将A的各列元素分别乘以对角阵的对角线元素,如何实现?
>> A*D
ans =
7 0 3 0 25
3 10 21 16 5
4 0 9 0 10
1 2 27 8 15
1 16 15 8 45
2.三角阵
上三角阵:矩阵的对角线以下的元素全为零的矩阵。
upper triangular matrix
下三角阵:对角线以上的元素全为零的矩阵。
上三角阵
triu(A):提取矩阵A的主对角线及以上的元素。
triu(A,k):提取矩阵A的第k条对角线及以上的元素。
>> triu(ones(4),-1)
ans =
1 1 1 1
1 1 1 1
0 1 1 1
0 0 1 1 其中,ones函数产生四阶全1矩阵。
下三角阵
在MATLAB中,提取矩阵A的下三角矩阵的函数是tril,其用法与triu函数完全相同。
3.矩阵的转置
转置运算符是小数点后面接单引号 .'
共轭转置,其运算符是单引号 ' ,它在转置的基础上还要取每个数的复共轭。
>> A=[1,3;3+4i,1-2i]
A =
1 + 0i 3 + 0i
3 + 4i 1 - 2i
>> A.'
ans =
1 + 0i 3 + 4i
3 + 0i 1 - 2i
>> A'
ans =
1 + 0i 3 - 4i
3 + 0i 1 + 2i
4.矩阵的旋转
rot90(A,k):将矩阵A逆时针方向旋转90度的k倍,当k为1时可省略。
>> A=[1,3,2;-3,2,1;4,1,2]
A =
1 3 2
-3 2 1
4 1 2
>> rot90(A)
ans =
2 1 2
3 2 1
1 -3 4
>> rot90(A,2)
ans =
2 1 4
1 2 -3
2 3 1
5.矩阵的翻转
所谓左右翻转,是,第一列最后一列调换,第二列和倒数第二列调换,以此类推。
所谓上下翻转,是 行 行
fliplr(A):对矩阵A实施左右翻转。
flipud(A):对矩阵A实施上下翻转。
例子:验证魔方阵的主对角线、副对角线元素之和相等。
>> A=magic(5);
>> D1=diag(A);
>> sum(D1)
ans =
65
>> B=flipud(A);
>> D2=diag(B);
>> sum(D2)
ans =
65
6.矩阵的求逆
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵 。
inv(A):求方阵A的逆矩阵。
例子:
>> A=[1,2,3;1,4,9;1,8,27];
>> b=[5;-2;6];
>> x=inv(A)*b
x =
23
-29/2
11/3
//也可以是直接A左除b
>> x=A\b
x =
23
-29/2
11/3
三、矩阵求值
矩阵的行列式值
矩阵的秩
矩阵的迹
矩阵的范数
矩阵的条件数
1.方阵的行列式
把一个方阵看作一个行列式,并对其按行列式的规则求值,这个值就称为方阵所对应的行列式的值。
det(A):求方阵A所对应的行列式的值。
>> A=[1,3,2;-3,2,1;4,1,2]
A =
1 3 2
-3 2 1
4 1 2
>> det(inv(A))
ans =
1/11
>> 1/det(A)
ans =
1/11
2.矩阵的秩
矩阵线性无关的行数或列数称为矩阵的秩。
rank(A):求矩阵A的秩。
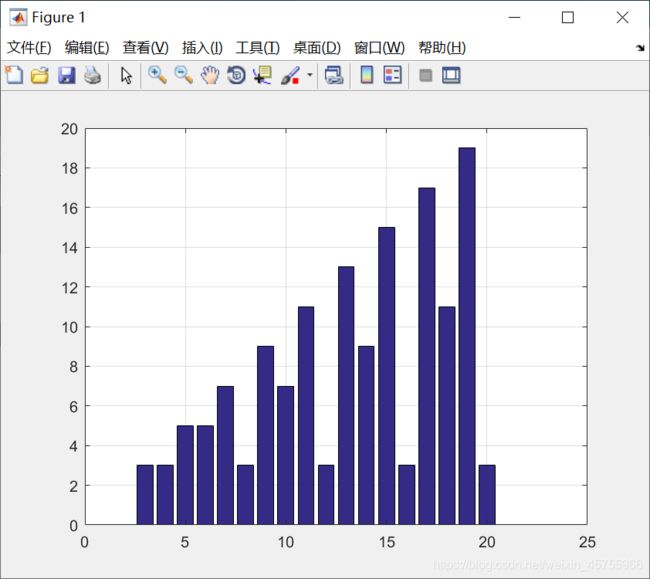
例子:求3~20阶魔方阵的秩。
for n =3:20
r(n)=rank(magic(n));
end
bar(r)
grid on
axis(2,2130,20)输出结果
3.矩阵的迹
矩阵的迹等于矩阵的对角线元素之和,也等于矩阵的特征值之和。
trace(A):求矩阵A的迹。
>> A=[1,3,2;-3,2,1;4,1,2]
A =
1 3 2
-3 2 1
4 1 2
>> b=trace(A)
b =
5
>> t=sum(diag(A))
t =
5
4.向量和矩阵的范数
矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。
向量的三种常用范数:
向量1—范数:向量元素的绝对值之和。
向量2—范数:向量元素绝对值的平方和的平方根。
向量无穷—范数:所有向量元素绝对值中的最大值。
norm(V)或norm(V,2):九三向量V的2—范数。
norm(V,1):计算向量V的1—范数。
norm(V,inf):计算向量V的无穷—范数。
矩阵的范数
从属于3种向量范数,矩阵范数计算公式如下。
矩阵A的1—范数:矩阵列元素绝对值之和的最大值。
矩阵A的2—范数:A’A矩阵的最大特征值的平方根。
其中拉姆达1为A‘A的最大特征值。
矩阵A的无穷—范数:所有矩阵行元素绝对值之和的的最大值。
MATLAB提供了三种求矩阵范数的函数,其函数调用格式与求向量的范数的函数完全相同。
>> x=[2 0 1;-1 1 0;-3 3 0]
x =
2 0 1
-1 1 0
-3 3 0
>> n=norm(x)
n =
5909/1251
>> n=norm(x,1)
n =
6
5.矩阵的条件数
矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积。
条件数越接近于1,矩阵的性能越好,反之,矩阵的性能越差。
在MATLAB中,计算矩阵A的三种条件数的函数是:
cond(A,1):计算A的1—范数下的条件数。
cond(A)或cond(A,2):计算A的2—范数下的条件数。
cond(A,inf):计算A的无穷—范数下的条件数。
例子:
求2~10阶希尔伯特矩阵的条件数。
for n=2:10
c(n)=cond(hilb(n));
end
format long
c'
//输出结果
>> Untitled3
ans =
1.0e+13 *
0
0.000000000001928
0.000000000052406
0.000000001551374
0.000000047660725
0.000001495105864
0.000047536735691
0.001525757556663
0.049315340455101
1.602502816811318
四、矩阵的特征值与特征向量
1.矩阵特征值的数学定义
设 A 是n阶方阵,如果存在数m和非零n维列向量 x,使得 Ax=mx 成立,则称 m 是矩阵A的一个特征值(characteristic value)或本征值(eigenvalue)。
函数调用格式有两种:
E=eig(A):求矩阵A的全部特征值,构成向量E。
[X,D]=eig(A):求矩阵A的全部特征值,构成对角阵D并产生矩阵X,X各列是相应的特征向量。
A =
1 3 2
-3 2 1
4 1 2
>> [X,D]=eig(A)
X =
1 至 2 列
-0.076924121145930 + 0.302382386347883i -0.076924121145930 - 0.302382386347883i
-0.626744812952564 - 0.072839067736789i -0.626744812952564 + 0.072839067736789i
0.710304851215854 + 0.000000000000000i 0.710304851215854 + 0.000000000000000i
3 列
0.415425551450934 + 0.000000000000000i
-0.223488190426173 + 0.000000000000000i
0.881745223940409 + 0.000000000000000i
D =
1 至 2 列
0.684450351230506 + 1.600285392545227i 0.000000000000000 + 0.000000000000000i
0.000000000000000 + 0.000000000000000i 0.684450351230506 - 1.600285392545227i
0.000000000000000 + 0.000000000000000i 0.000000000000000 + 0.000000000000000i
3 列
0.000000000000000 + 0.000000000000000i
0.000000000000000 + 0.000000000000000i
3.631099297538989 + 0.000000000000000i
例子:
程序代码:
R=[-1,2,0;2,-4,1;1,1,-6];
S=[1,2;2,3];
A=[R,zeros(3,2);zeros(2,3),S];
[X1,d1]=eig(R)
[X2,d2]=eig(S)
[X3,d3]=eig(A)
//输出:
>> Untitled3
X1 =
0.855336847706575 0.451748808798346 0.189889692402449
0.470284611344323 -0.839453879712591 -0.511105640718618
0.217327543786097 -0.302059923830942 0.838279743728139
d1 =
0.099647729675864 0 0
0 -4.716463058067783 0
0 0 -6.383184671608076
X2 =
-0.850650808352040 0.525731112119133
0.525731112119133 0.850650808352040
d2 =
-0.236067977499790 0
0 4.236067977499790
X3 =
0.855336847706575 0.451748808798346 0.189889692402449 0 0
0.470284611344323 -0.839453879712591 -0.511105640718618 0 0
0.217327543786097 -0.302059923830942 0.838279743728139 0 0
0 0 0 -0.850650808352040 -0.525731112119133
0 0 0 0.525731112119133 -0.850650808352040
d3 =
0.099647729675864 0 0 0 0
0 -4.716463058067783 0 0 0
0 0 -6.383184671608076 0 0
0 0 0 -0.236067977499790 0
0 0 0 0 4.236067977499790
2.特征值的集合意义
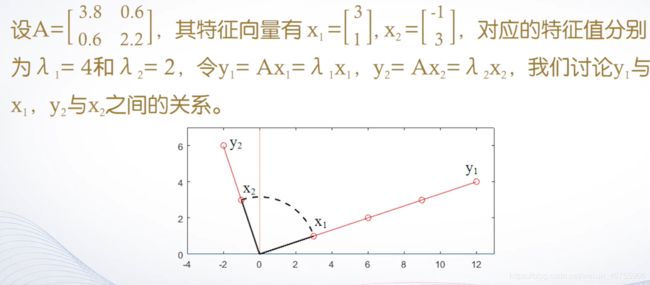
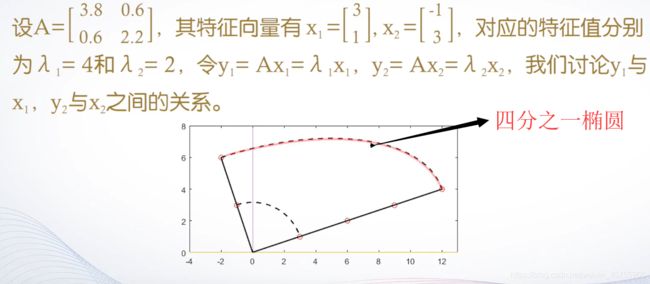
MATLAB提供了一个eigshow函数,可以演示单位圆上的向量x和Ax之间的关系,其运行画面如图所示。
例子:
x=[0,0.5,0.5,3,5.5,5.5,6,6,3,0;0,0,6,0,6,0,0,8,1,8];
A=[1,0.5;0,1];
y=A*x;
subplot(2,2,1);
fill(x(1,:),x(2,:),'r');
subplot(2,2,2);
fill(y(1,:),y(2,:),'r');输出结果:
五、稀疏矩阵
矩阵的存储方式
稀疏存储方式的产生
稀疏矩阵的应用实例
1.矩阵的存储方式
完全存储方式
稀疏存储方式
稀疏存储方式只存储矩阵的非零元素的值及其位置,即行号和列号。
注意,采用稀疏存储方式时,矩阵元素的存储顺序并没有改变,也是按列的顺序进行存储。
2.稀疏存储方式的产生
完全存储方式与稀疏存储方式之间的转化
A=sparse(S):将矩阵S转化为稀疏存储方式的矩阵A。
S=full(A):将矩阵A转化为完全存储方式的矩阵S。
>> A=sparse(eye(5))
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
>> B=full(A)
B =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> whos
Name Size Bytes Class Attributes
A 5x5 128 double sparse
B 5x5 200 double
直接建立稀疏存储矩阵
sparse函数的其他调用格式:
sparse(m,n):生成一个m*n的所有元素都是零的稀疏矩阵。
sparse(u,v,S):其中u、v、S是3个等长的向量。S是要建立的稀疏存储矩阵的非零元素,u(i)、v(i)分别是S(i)的行和列下标。
>> A=sparse([1,2,2],[2,1,4],[4,5,-7])
A =
(2,1) 5
(1,2) 4
(2,4) -7
>> B=full(A)
B =
0 4 0 0
5 0 0 -7
使用spconvert函数直接建立稀疏存储矩阵,其调用格式为:
B=spconvert(A)
A为一个m*3或m*4的矩阵,其每行表示一个非零元素,m是非零元素的个数。
A(i,1)表示第i个非零元素所在的行。
A(i,2)表示第i个非零元素所在的列。
A(i,3)表示第i个非零元素值的实部。
A(i,4)表示第i个非零元素值得虚部。
若矩阵得全部元素都是实数,则无需第四列。
例子:
>> A=[2,2,1;2,1,-1;2,4,3]
A =
2 2 1
2 1 -1
2 4 3
>> B=spconvert(A)
B =
(2,1) -1
(2,2) 1
(2,4) 3
带状稀疏矩阵得稀疏存储
稀疏矩阵有两种基本类型:无规则结构得稀疏矩阵与有规则结构得稀疏矩阵。
带状稀疏矩阵是指所有非零元素集中在对角线上得矩阵。
[B,d]=spdiags(A):从带状稀疏矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线得位置向量d。
A=spdiags(B,d,m,n):产生带状稀疏矩阵的稀疏存储矩阵A,其中m,n为原带状稀疏矩阵的行数与列数,矩阵B的第i列即为原带状稀疏矩阵的第i条非零对角线,向量d为原带状稀疏矩阵所有非零对角线的位置。
>> A=[11,0,0,12,0,0;0,21,0,0,22,0;0,0,31,0,0,32;41,0,0,42,0,0;0,51,0,0,52,0]
A =
11 0 0 12 0 0
0 21 0 0 22 0
0 0 31 0 0 32
41 0 0 42 0 0
0 51 0 0 52 0
>> [B,d]=spdiags(A)
B =
0 11 12
0 21 22
0 31 32
41 42 0
51 52 0
d =
-3
0
3
>> A=spdiags(B,d,5,6)
A =
(1,1) 11
(4,1) 41
(2,2) 21
(5,2) 51
(3,3) 31
(1,4) 12
(4,4) 42
(2,5) 22
(5,5) 52
(3,6) 32
单位矩阵的稀疏存储
speye(m,n)返回一个m*n的稀疏存储单位矩阵。
>> speye(3)
ans =
(1,1) 1
(2,2) 1
(3,3) 1
例子:
代码:
>> kf1=[1;1;2;1;0];
>> k0=[2;4;6;6;1];
>> k1=[0;3;1;4;2];
>> B=[kf1,k0,k1];
>> d=[-1;0;1];
>> A=spdiags(B,d,5,5);
>> f=[0;3;2;1;5];
>> x=A\f
x =
-0.1667
0.1111
2.7222
-3.6111
8.6111
注意:当参与运算的数据对不全是稀疏存储矩阵时,所得结果是完全存储形式。