学习笔记——优先队列和堆排序
优先队列
优先队列是一种特殊的数据结构,它支持两种重要的操作:删除最大元素和插入元素。
通过插入一系列元素然后一个一个删除,我们可以通过优先队列实现排序算法。
API
| API名称 | 说明 |
|---|---|
| Insert(int) | 插入一个元素 |
| Max() int | 返回最大的元素 |
| DelMax() int | 弹出最大元素 |
| IsEmpty() bool | 返回队列是否为空 |
| Size() int | 返回队列中元素的个数 |
初级实现
我们可以使用有序或无序的数组和链表实现优先队列。
- 通过改动删除元素的函数使它在删除的时候寻找最大的元素进行删除,这种实现被成为“惰性方法”——因为它尽在有必要的时候才采取行动。
- 另一种“积极方法”是在插入元素的时候就将元素插入到相应的位置,整个序列始终保持有序。
数组实现
我们使用一个go语言中的切片实现一个栈,然后将这个栈稍做改造即可实现优先队列:在弹出元素的时候先在栈中寻找最大的元素,然后把它和栈顶的元素交换,这样弹出来的就是最大的元素。以下是这种实现的部分代码(省略了几个简单的函数,全部代码在文末的GitHub仓库):
func (q PQ_array) Max() int {
max, _ := q.max()
return max
}
// 内部函数
// 遍历找出当前最大的元素和它的索引并返回
func (q PQ_array) max() (int, int) {
max, j := q.a[0], 0
for i := 1; i < len(q.a); i++ {
if q.a[i] > max {
max = q.a[i]
j = i
}
}
return max, j
}
// 将最大的元素和末尾元素交换并弹出最后的元素
func (q *PQ_array) DelMax() int {
max, j := q.max()
tmp := q.a[j]
q.a[j] = q.a[q.length-1]
q.a[q.length-1] = tmp
q.a = q.a[:q.length-1]
q.length--
return max
}
编写一个测试脚本进行测试:
func main() {
q := maxpq.PQ_array{}
a := []int{2, 4, 9, 1, 3, 96, 100, 34, 54}
for _, n := range a {
q.Insert(n)
}
fmt.Println(q.DelMax())
fmt.Println(q.Size())
fmt.Println(q.Max())
}
测试结果:
MacBook-Pro-2:优先队列 bbfat$ go run main.go
100
8
96
数组实现是一种“惰性方法”。
链表实现
我们这次来创作一个“积极方法”——在插入元素的时候就将其排序,由于数组的特性,进行这个操作需要移动许多元素,比较浪费,此时链表的优势就体现出来了:在任何位置插入元素的时间复杂度都是O(1)。
type PQ_list struct {
head *node
length int
}
type node struct {
val int
next *node
}
func (q *PQ_list) Insert(e int) {
p1, p2 := q.head, q.head
for p1 != nil && e < p1.val {
p2 = p1
p1 = p1.next
}
new := node{e, p1}
if p1 != p2 {
p2.next = &new
} else {
q.head = &new
}
q.length++
}
func (q PQ_list) Max() int {
return q.head.val
}
// 将最大的元素和末尾元素交换并弹出最后的元素
func (q *PQ_list) DelMax() int {
p := q.head.next
val := q.head.val
q.head = p
q.length--
return val
}
基于二叉堆实现优先队列
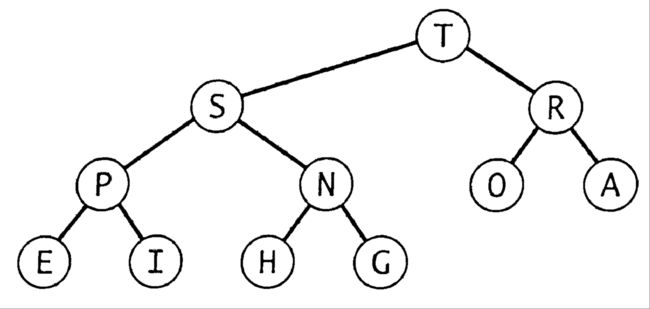
二叉堆(以下简称堆)是一种基于二叉树的数据结构。在堆中,每个元素都要保证能大于等于他的两个孩子元素。
- 当一颗二叉树的每个节点都大于等于它的两个子节点时,它被称为堆有序。
- 跟节点是堆有序的二叉树中最大的节点。
二叉堆的表示方法
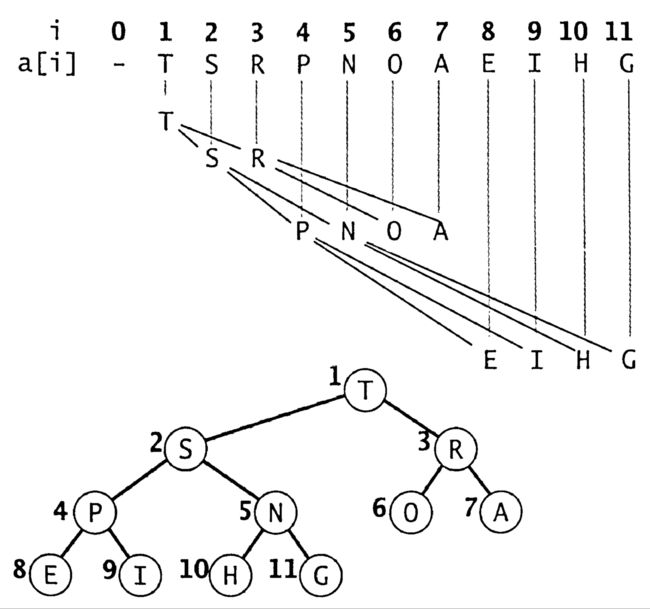
我们可以使用结构指针来表示堆有序的二叉树,每个元素都需要三个指针来找到它的父节点和子节点。但其实在这个问题中我们构造的是一颗完全二叉树,这使得我们的表示方法变得特别简单——用数组表示。具体方法是将二叉树的节点按照层级顺序放入数组中,根节点的位置在1,他的子节点位置在2和3。
- 二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级顺序存储(不实用数组的0索引位置)。
二叉堆的重要性质
- 位置为k的节点的父节点的位置为k/2
- 位置为k的节点的子节点的位置为k/2和k/2+1
上浮算法
如果堆的有序状态因为某个节点变得比他的父节点更大而被打破,那么我们就需要将这个节点上浮到合适的位置,上浮一次之后这个节点还是有可能比它的父节点大,我们就继续将它上浮,直到它比它的父节点小或它到达根节点为止。
type PQ_heap struct {
a []int
length int
}
func (q *PQ_heap) swim(k int) {
for k > 1 && q.a[k/2] < q.a[k] {
exch(q.a, k/2, k)
k /= 2
}
}
下沉算法
如果某个节点变得比它的两个子节点或其中之一更小,那么我们需要将它下沉到合适的位置。
先选出子节点中最大的那个,然后将它和子节点交换,然后继续向下寻找,直到该节点比两个子节点都大为止。
func (q *PQ_heap) sink(k int) {
for k*2 <= q.length {
j := k * 2
// 比较k的两个孩子谁更大
if j < q.length && q.a[j] < q.a[j+1] {
j++
}
// 如果k小于它最大的孩子则下沉结束
if !(q.a[k] < q.a[j]) {
break
}
exch(q.a, k, j)
k = j
}
}
插入元素
我们将新元素加到数组末尾,增加堆的大小并让这个新元素上浮到合适的位置。
func (q *PQ_heap) Insert(e int) {
if q.length == 0 {
q.a = append(q.a, 0, e)
} else {
q.a = append(q.a, e)
}
q.length++
q.swim(q.length)
}
[外链图片转存失败(img-c5oSFmr1-1566978263225)(https://img.hacpai.com/file/2019/08/image-124f1381.png)]
删除最大元素
我们从数组顶端删去最大的元素并将数组的最后一个元素放到顶端,减小堆的大小并让这个元素下沉到合适的位置。
// 将最大的元素和末尾元素交换并弹出最后的元素
func (q *PQ_heap) DelMax() int {
max := q.a[1]
q.a[1] = q.a[q.length]
q.a = q.a[:q.length]
q.length--
q.sink(1)
return max
}
- 对于一个含有N个元素基于堆的优先队列,插入元素操作只需不超过(lgN+1)次比较,删除最大元素的操作需要不超过2lgN次比较。
堆排序
func Sort(a []int) {
n := len(a)
for k := n / 2; k >= 1; k-- {
sink(a, k, n)
}
for n > 1 {
exch(a, 1, n)
n--
sink(a, 1, n)
}
}
func sink(a []int, k, n int) {
for k*2 <= n {
j := k * 2
if j < n && a[j] < a[j+1] {
j++
}
if !(a[k] < a[j]) {
break
}
exch(a, k, j)
k = j
}
}
第一个for循环构造了堆:
第二个for循环将最大的元素a[1]和a[n]交换并修复了堆,如此往复,直到堆变为空。
总结
堆排序在排序复杂性的研究中有着重要的地位,因为它是我们所知的唯一能够同时最优地利用空间和时间的方法—在最坏的情况下它也能保证使用~2NlgN次比较和恒定的额外空间。但现代系统的许多应用很少使用它,因为它无法利用缓存。数组元素很少和相邻的其他元素进行比较,因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法,如快速排序、归并排序,甚至是希尔排序。
另一方面,用堆实现的优先队列在现代应用程序中越来越重要,因为它能在插入操作和删除最大326元素操作混合的动态场景中保证对数级别的运行时间。
本节代码