《数据分析与挖掘 第六章 电力窃漏电用户自动识别系统》

电力窃漏电用户自动识别系统

数据预处理
有一张含有若干缺失值的表格，需要用拉格朗日插值法，将缺失值补齐:
这是三个用户的用电情况

import pandas as pd
from scipy.interpolate import lagrange

inputfile = 'missing_data.xls'

data = pd.read_excel(inputfile,header = None)
data1 = data.copy()

#自定义列向量插值函数
#s为列向量，n为被插值的位置，k为取前后的数据个数，默认5
def ployinterp_column(s,n,k = 5):
    y = s[list(range(n-k,n)) + list(range(n+1,n+1+k))]#前后各取k个数
    #print(y)
    y = y[y.notnull()]#剔除空值
    #print(y,y.index)
    return lagrange(y.index , list(y))(n)#插值并返回插值结果

#逐个元素判断是否需要插值
for i in data.columns:
    for j in range(len(data)):
        if (data[i].isnull())[j]:
            #print(i , ' ' , j)
            data[i][j] = ployinterp_column(data[i],j)

我们可以清楚的看出处理过程：
如在0列5行是nan：

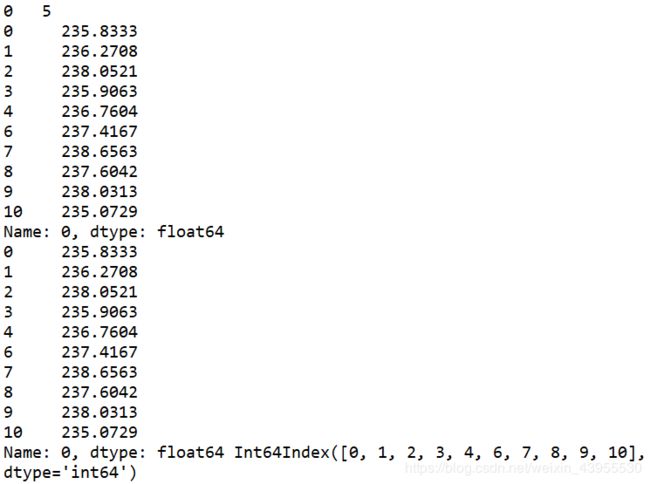
取了前五个数和后五个数，然后这是个数里面都没有空值，所以剔除空值之后还是十个数
然后用拉格朗日插值算了该出的值

再比如，在1列20行这里的空值，前后各取了五个数，但是这总共十个数中有空值，剔除了之后还剩五个值，用这5个点算该出的值

outputfile = 'missing_data_processed.xls'
data.to_excel(outputfile,header = None,index = False)

保存到xls格式

创建专家样本
补齐了空缺值之后，通过历史的用户的用电量情况和一些指标，如电量趋势下降指标，线损指标，警告类指标，以及是否是真的偷窃电，有一个样本，叫做专家样本，这个专家样本是为了给我们训练模型的，训练出模型了，就可以通过现有的监控的用户用电情况，预测出他是否有窃电行为

import numpy as np
import pandas as pd
from random import shuffle #导入随机函数shuffle

datafile = 'model.xls'
data = pd.read_excel(datafile) 
#如果表格有指定每列属性名，就不写“headeer = None”，属性名自动成为列名index
#header = None表示index没有名字用0,1,2...表示，不加这一行，自动将表格第一行变成index
data = np.mat(data)#将表格转为矩阵形式
data1 = data.copy()#作为打乱的对比，打乱之前的样子
shuffle(data)#随机打乱

p = 0.8#设置训练数据的比例
train = data[:int(len(data)*p),:]#前80%作为训练集
test = data[int(len(data)*p):,:]#后20%作为测试集

我们可以把没有打乱的data，copy到的data1与shuff打乱之后的data进行对比：

测试集和训练集的数据大小查看一下：

构建模型

• 构建LM神经网络模型

import numpy as np
import pandas as pd
from random import shuffle #导入随机函数shuffle

datafile = 'model.xls'
data = pd.read_excel(datafile) 
#如果表格有指定每列属性名，就不写“headeer = None”，属性名自动成为列名index
#header = None表示index没有名字用0,1,2...表示，不加这一行，自动将表格第一行变成index
data = np.mat(data)#将表格转为矩阵形式
data1 = data.copy()#作为打乱的对比，打乱之前的样子
shuffle(data)#随机打乱

p = 0.8#设置训练数据的比例
train = data[:int(len(data)*p),:]#前80%作为训练集
test = data[int(len(data)*p):,:]#后20%作为测试集

#构建LM神经网络模型
from keras.models import Sequential #导入神经网络初始化函数
from keras.layers.core import Dense, Activation #导入神经网络层函数、激活函数

netfile = 'net.model' #构建的神经网络模型存储路径

net = Sequential() #建立神经网络
net.add(Dense(input_dim = 3, output_dim = 10)) #添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu')) #隐藏层使用relu激活函数
net.add(Dense(input_dim = 10, output_dim = 1)) #添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid')) #输出层使用sigmoid激活函数
net.compile(loss = 'binary_crossentropy', optimizer = 'adam') #编译模型，使用adam方法求解

net.fit(train[:,:3], train[:,3], epochs=10, batch_size=1) #训练模型，循环10次
net.save_weights(netfile) #保存模型

predict_result = net.predict_classes(train[:,:3]).reshape(len(train)) #预测结果变形

可以看出10次训练的结果，loss在逐渐减少，如果进行100次：

最后的loss稳定在0.31的样子
十次训练的预测结果：

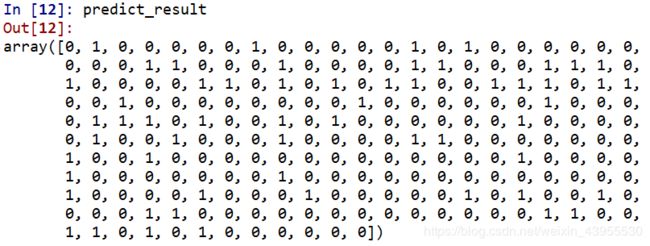
这看起来是一个array，其实是一个n*1的数

模型也保存下来了
接下来用混淆矩阵可视化：

from cm_plot import * #导入自行编写的混淆矩阵可视化函数
cm_plot(train[:,3], predict_result).show() #显示混淆矩阵可视化结果

cm_plot:

def cm_plot(y, yp):
  
  from sklearn.metrics import confusion_matrix #导入混淆矩阵函数

  cm = confusion_matrix(y, yp) #混淆矩阵
  
  import matplotlib.pyplot as plt #导入作图库
  plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
  plt.colorbar() #颜色标签
  
  for x in range(len(cm)): #数据标签
    for y in range(len(cm)):
      plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
  
  plt.ylabel('True label') #坐标轴标签
  plt.xlabel('Predicted label') #坐标轴标签
  return plt

• 构建CART决策树模型

import pandas as pd
from random import shuffle

datafile = 'model.xls'
treefile = 'tree.pkl'

data = pd.read_excel(datafile) #读取数据，数据的前三列是特征，第四列是标签
data = data.values #将表格转换为矩阵
shuffle(data) #随机打乱数据

p = 0.8 #设置训练数据比例
train = data[:int(len(data)*p),:] #前80%为训练集
test = data[int(len(data)*p):,:] #后20%为测试集

###这里之前都是一样的，打散数据分成训练集和测试集###

from sklearn.tree import DecisionTreeClassifier #导入决策树模型
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数

tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(train[:,:3],train[:,3]) #训练

#保存模型
from sklearn.externals import joblib
joblib.dump(tree, treefile) 

predict_result = tree.predict(train[:,:3])

在tree中tree.predict就是预测分类了，与LM神经网络不同，神经网络net.predict是预测概率，net.predict_classes才是预测分类

这是预测的结果
画出混淆矩阵：

cm = confusion_matrix(train[:,3], tree.predict(train[:,:3])) #混淆矩阵

import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
plt.colorbar() #颜色标签

for x in range(len(cm)): #数据标签
  for y in range(len(cm)):
    plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')

plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
plt.show() #显示作图结果


模型评价
除了混淆矩阵还可以用ROC曲线
用测试样本进行评估

from sklearn.metrics import roc_curve #导入ROC曲线函数
import matplotlib.pyplot as plt
predict_result = net.predict(test[:,:3]).reshape(len(test))
fpr, tpr, thresholds = roc_curve(test[:,3], predict_result, pos_label=1)
#fps和tps就是混淆矩阵中的FP和TP的值
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of LM') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果

对于CART树

from sklearn.metrics import roc_curve #导入ROC曲线函数

fpr, tpr, thresholds = roc_curve(test[:,3], tree.predict_proba(test[:,:3])[:,1], pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'green') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果

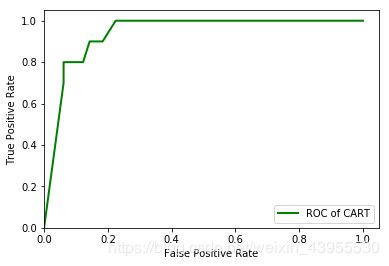
我们得到了LM神经网络训练100次和CART树分类之后的ROC图，怎么通过ROC来看模型好坏呢？
看那个ROC线下的面积更大，即更靠近正方形左上角，就说明该模型更适用
目前看来，CART树模型似乎更适合
但如果LM神经网络，训练1000次：

这样看，神经网络训练1000次的模型似乎有更好一些

用保存好的模型直接去预测以后来的数据，就不用在训练了