《动手学深度学习》Pytorch版学习打卡 (一)

背景：

有python和机器学习的基础，深度学习方面基础基本为0，了解到开源组织Datawhale和伯禹学习平台以及K-Lab合作推出了《动手学深度学习》这本书的Pytorch版代码讲解，就报名参加了。

学习资料：

《动手学深度学习》Pytoch版Github开源项目
Datawhale+伯禹学习平台网课

学习前的基础了解：

需要了解神经网络的一些基本概念、反向传播算法等
深度学习之反向传播算法

学习方法：

1.先看平台准备的Jupyter文件，搜集一些相关资料，了解知识点理论基础。
2.看视频里的代码讲解，将视频里听到的重点注释在下载的代码旁
3.搜集资料，看《动手学》原书，查漏补缺

第一次打卡内容

1. 用Pytorch实现一个线性回归

关键词：线性回归、矢量计算、单层神经网络、Pytoch的简洁实现

这里默认已经有了一定的线性回归算法的理论基础，主要就是线性回归的模型定义、损失函数、优化算法，没有的可以看书中关于线性回归的描述：线性回归的基本要素
用神经网络来表示一个线性回归主要表示为以下结构：

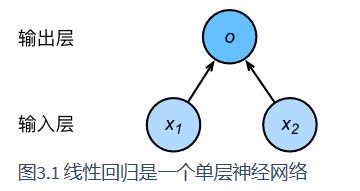
按照惯例神经网络的层数是指涉及计算的层的数量，这里只有输出层涉及到计算，因此这是一个单层的神经网络，同时，输出层的的神经元又和输入层的各个单元完全连接，因此输出层又是一个全连接层

矢量计算的优势：
我们可以通过如下代码了解矢量运算相比标量计算的速度优势

timer = Timer()
c = torch.zeros(n)
for i in range(n):
    c[i] = a[i] + b[i]
'%.5f sec' % timer.stop()

‘0.01188 sec’

timer.start()
d = a + b
'%.5f sec' % timer.stop()

‘0.00024 sec’
很明显后者的运算速度快很多，因此在计算中应尽量使用矢量计算方式

从0实现线性回归代码，运用Pytorch实现线性回归的代码在原书在线版都有，不详细贴出，可以从中大概总结出用Pytorch训练一个神经网络的基本步骤

• 读取数据（线性回归这次课中用的Pytorch中的utils.data模块）
• 定义模型
  做法1.继承torch.nn中的module，自己撰写网络/层，要定义类属性、函数、前向传播算法forward等。示意：
  做法2.使用nn.Sequential。Sequential是一个有序的容器，网络层将按照在传入Sequential的顺序依次被添加到计算图中。写法一示意：
• 初始化模型参数（多种初始化方法，一般用init模块进行初始化，这里要初始化的参数为权重W和偏差b
• 定义损失函数（nn模块中有很多损失函数）
• 定义优化算法（torch.optim提供了很多优化算法，比如就有小批量随机梯度下降算法SGD,还可以设置学习率

import torch.optim as optim

optimizer = optim.SGD([
               # 如果对某个参数不指定学习率，就使用最外层的默认学习率
               {'params': net.subnet1.parameters()}, # lr=0.03
               {'params': net.subnet2.parameters(), 'lr': 0.01}
           ], lr=0.03)

• 训练模型：在上述步骤完成后就可以开始传入训练了

num_epochs = 3
for epoch in range(1, num_epochs + 1):
   for X, y in data_iter:
       output = net(X)
       l = loss(output, y.view(-1, 1))
       optimizer.zero_grad() # 梯度清零，等价于net.zero_grad()
       l.backward()
       optimizer.step()
   print('epoch %d, loss: %f' % (epoch, l.item()))

需要注意的是要制定epochs次数，还要进行梯度清零，反向传播

以上就是使用Pytorch进行线性回归建模的学习笔记

2.Softmax回归与分类任务

在了解Softmax前要先简单了解一下分类任务，分类与回归的区别就是，

回归是给出预测的“值”，分类给出的是预测的“类别”。

softmax回归与分类的关系就是softmax回归输出的值的个数等于类别的个数，即softmax回归输出的值是预测为这三个类别分别的可能性，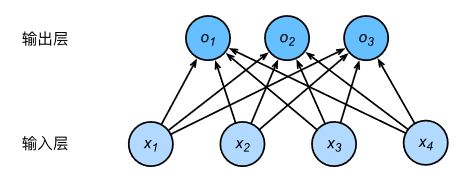
一般的办法就是将输出的值作为预测成这三个类别的置信度，值最大的类别为预测类别，但直接这样做的办法会带来问题，因为值为离散值，范围不确定，因此很难衡量，所以这里引入Softmax运算符

这里面exp(o)是以e为底数,o为指数的幂函数，通过这样的转换可以将原来的输出转换为一个(0,1)之间的概率分布，比如y₂ = 0.8，那么预测为类别2的概率就是80%

softmax回归计算表达式：

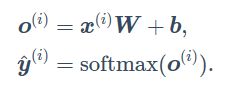
代码部分：
从0实现Softmax代码与使用Pytorch的简洁实现
其中涉及到的一些关于代码的细节可以通过看网课自行记录，和线性回归建模的步骤大同小异。
要注意的地方举例：

• 对于图像数据转换为tensor的步骤
• 简洁实现里定义网络模型时要定义一个额外的转换层

以上是关于Softmax回归的学习笔记

3.多层感知机（MLP）

对比于单层神经网络，多层感知机的区别就在于多了隐藏层（hidden layer）让输入层的输出作为隐藏层的输入，隐藏层的输出再作为输出层的输入

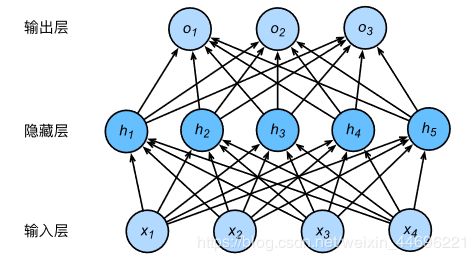
可以看出这个多层感知机中隐藏层和输出层都是全连接层，权重矩阵W共有45+53个元素
由于输入层的输出作为隐藏层的输入，隐藏层的输出再作为输出层的输入。隐藏层和输出层的输出分别可以用如下式子表示：

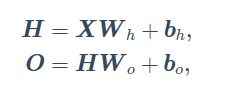
我们将其联立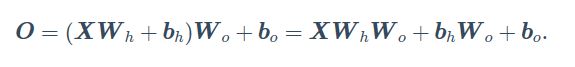
发现这还是一个单层神经网络的表达式，所以如果不做一些什么，即使有再多隐藏层，这个网络也还是相当于一个单层神经网络。
解决的办法就是为隐藏层添加一个非线性变换，即激活函数（activation function）

添加了激活函数后，多层感知机按照如下方式进行计算：

在分类问题中，我们可以对输出O做softmax运算，并使用softmax回归中的交叉熵损失函数。
在回归问题中，我们将输出层的输出个数设为1，并将输出O直接提供给线性回归中使用的平方损失函数

常见的激活函数：

• ReLU
  
  
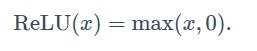
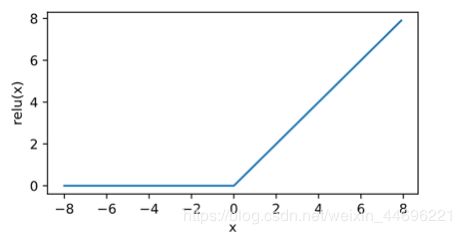
  即当x大于0时才等于本身
• sigmoid函数
  
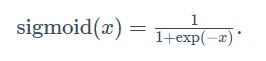
  sigmoid函数可以将元素的值变换到0到1之间，在早期的神经网络中比较常见，但现在逐渐被ReLU函数取代，因为他计算开销比较大
  
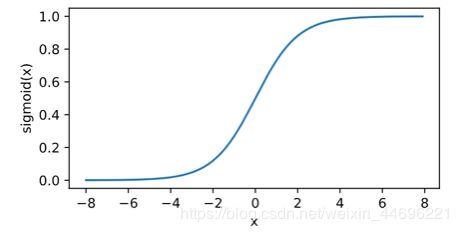
• tanh（双曲正切）函数
  tanh（双曲正切）函数可以将元素的值变换到-1和1之间：
  
  

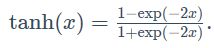
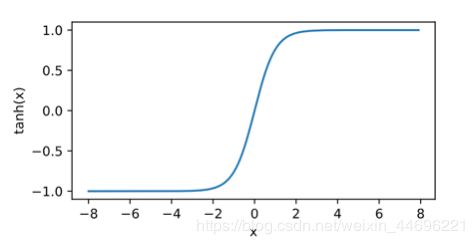
代码部分：
从0实现多层感知机和简洁实现多层感知机
和实现Softmax部分代码大同小异
不同的地方举例：

• 定义模型参数时多了隐藏层的参数
• 比起单层网络还需要定义激活函数

以上就是多层感知机的学习笔记

4.文本预处理

文本预处理是自然语言处理中重要的一步
就是为了将自然的文本处理成计算机能够处理的初步状态
简单的预处理主要包含以下几步：

• 读入文本
• 分词（分词工具如spaCy，NLTK，中文分词工具jieba）
• 去重，建立字典（即将每个词映射到一个唯一的索引形式）
• 将文本中的每一个词根据字典转换为索引的形式

文本预处理主要就是为了构建词典，最后的结果是得到了一个词与索引一一对应的词典，为语言模型做基础。

5.语言模型

基于统计的语言模型：

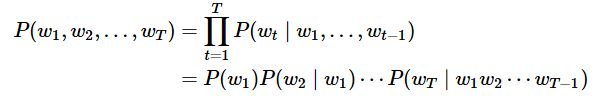
语言模型的参数就是词的概率以及给定前几个词情况下的条件概率。设训练数据集为一个大型文本语料库，如维基百科的所有条目，词的概率可以通过该词在训练数据集中的相对词频来计算，例如，w1的概率可以计算为：

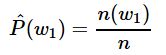
其中n(w1)为语料库中以w1作为第一个词的文本的数量，n为语料库中文本的总数量。类似的，给定w1w1情况下，w2w2的条件概率可以计算为：

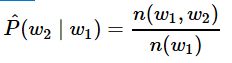
其中n(w1,w2)n(w1,w2)为语料库中以w1w1作为第一个词，w2w2作为第二个词的文本的数量。

n-元语法
n-元语法就是通过马尔可夫假设简化模型的一种方式，马尔科夫假设是指一个词的出现只与前面n个词相关，即n阶马尔可夫链（Markov chain of order nn），如果n=1，那么有
n-元语法是基于n−1阶马尔可夫链的概率语言模型。例如，当n=2时，含有4个词的文本序列的概率就可以改写为：

n-元语法的缺陷：参数空间过大，数据稀疏

语言模型数据集
建立语言模型数据集的做法就是读入文本，建立字符到索引的映射，这在文本预处理中提到，特殊的地方在于文本数据的读取。
文本数据属于时序数据。时序数据的一个样本通常包含连续的字符。假设时间步数为5，样本序列为5个字符，即“想”“要”“有”“直”“升”。该样本的标签序列为这些字符分别在训练集中的下一个字符，即X=“想要有直升”，Y=“要有直升机”。
我们主要采用如下两种方式对时序数据进行采样：

• 随机采样

1. batch_size是每个小批量的样本数，num_steps是每个样本所包含的时间步数。随机采样的核心步骤就是，先将样本空间-1，这是为了保证对于长度为n的数据，样本X只能由前n-1个字符。
2. 然后将-1剩下的样本 / num_steps，下取整，得到样本的个数，多出的样本舍去，然后根据batch_size，决定每个批量分别取这些样本中的几个样本。
3. 例如，对于0~29 共30个数，batch_size = 2 , num_steps = 6，计算（30-1）/6 下取整得4，即划分为
   [0,1,2,3,4,5] [6,7,8,9,10,11] [12,13,14,15,16,17] [18,19,20,21,22,23]
   然后每一个批量随机取其中两个样本，共可以取两个批量
   

• 相邻采样
  相邻采样的特点就是取出的两个随机小批量在原始序列上的位置相邻
  首先将样本数n划分成batch_size个，然后按照时间步长分别在这两个划分后的子集取样
  例如还是batch_size= 2 ， num_steps = 6，首先将0-29分成
  [0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10,11,12,13,14]
  [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]
  然后根据时间步长6从两个子集分别按顺序取出6个
  第一批取出
  
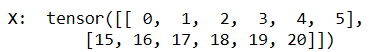
  第二批取出
  

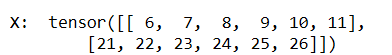
以上就是关于语言模型和两种采样方式的笔记

6.循环神经网络

关于神经网络的基础性知识整理：
循环神经网络基础
简单来说循环神经网络就是对于每一个隐藏层，除了当前输入层外，还有上一个隐藏层的状态信息（即状态H_t）共同作用于当前隐藏层

用公式描述就是：

H_t-1是上一个隐藏层的状态，W_xh是输入层的权重，W_hh是隐藏层之间的权重，在循环神经网络中，每个时间步共享参数W_xh、W_hh以及输出层权重W_qh

由于有了以上的特点，所以H_t能够捕捉截至当前时间步的序列的历史信息，就像是神经网络当前时间步的状态或记忆一样，然后通过计算当前步的输出，就可以进行预测下一步的信息。

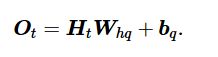
代码部分：
从0实现循环神经及简洁实现
需要注意到地方有：

• 将文本信息输入进循环神经网络除了建立词典，还需要将字符转化为向量，然后采样进模型。最简单的方式就是转化为one-hot向量，但带来的问题就是过于稀疏，造成维度灾难，现在一般用神经网络训练文本向量，如word2vec模型
• 循环神经网络容易造成梯度爆炸，可以进行梯度裁剪
• 用于评估模型，然后进行优化的指标叫困惑度，是对交叉熵损失函数指数运算得到的