PP预测（Forecast）功能中的常量预测模型（Constant Model）详解（重磅推荐）

PP预测（Forecast）功能中的常量预测模型（Constant Model）详解

作者：袁云飞（AlbertYuan）- 微信号yuanalbert

以下内容均为原创，希望对初学者有一些辅助作用，本人主要从事MM/QM/WM的相关工作，不专业处请多多指点，十足干货，码字不易，且行且珍惜，你们的关注就是我努力的动力，转载请引用出处，感激不尽；

PP模块里最不常用的物料计划功能就是—预测forecast；或许应该称为几乎不用的功能；

毕竟如果不了解其设计原则，运行管理，计算逻辑，适用范围得话，我们是没法精准推荐给用户使用的，而预测forecast这种计划的方式，往往在这几个方面都需要我们具备一定的专业知识了，不仅仅是IT技能，数学里的很多基础方法都将有助于我们理解SAP设计预测功能的初衷和原理；

而往往很多时候事与愿违，学信息化的人很难去从原理上去探索预测模型的数学来源，特别是要具备基于时间序列的分析这种数学方法，一般高等数学的知识是不足的；加上企业本身高速发展对于相关基础数据，参量等数据的沉淀较少，更难以使用；不过在了解了预测的基本原理后，小伙伴们应该就能深刻体会得到这些东西才是管理数据化，管理模型化，管理量化的魅力；下面我们从基础方向去带大家去尝试理解forecast；

物料计划是PP模块的一个重要组成部分，其核心要素在于通过不同的方式，对未来一段时间内预期的物料需求进行提前计划，从而根据相应的提前期进行有条不紊 的生产与采购活动。

在众多的物料计划方式中，MRP无疑是应用最为广泛的一种，这是因为MRP这种物料需求的计划方式逻辑清晰、容易理解、易于使用，且 MRP的顺利运行无需过多过严苛的先决条件。

同时，MRP的运算逻辑本身也十分合理、在功能上也强大，为企业物料计划员所广为接受。

MRP的物料计划方式是一种根据未来需求推算未来需求、以及根据未来需求推算未来供给的过程。

无论如何，我们一定要事先通过某种方式（如计划 独立需求、销售订单）将未来的物料需求给到系统，而后系统才能根据这些需求进行一系列的MRP运算。这样一来，当我们使用MRP的时候，就必须要花费一定 的工作量，找到一些可行的方法，将未来的物料需求输入到系统中。

因此可以说，虽然MRP的运行在很大程度上降低了计划员的工作量，但由于MRP本身以物料 需求的输入作为前提条件，则维护物料需求的工作量就是不可避免的。

除了最经典的MRP运算方式之外，还存在着另外一种物料计划方式，这就是预测（Forecast）。与MRP所不同的是，预测功能的本质 是根据过去的物料消耗值来推算未来的物料消耗值（即物料需求）。

在这种情况下，我们无需在系统中输入物料在未来的预期需求，系统就会直接根据物料在历史上 的消耗数据，自动推算出未来的物料需求。

预测功能在SAP系统中是一项非常高级与深入的功能，它可以实现物料需求推算的自动化、进而实现物料供给推算的自动化。我们再也不需绞尽脑汁地 去设想物料在未来的需求数据了，系统的自动运算会搞定一切。

不过，现实总是很残忍的；虽然预测功能是如此的高档与智能化，但真正在SAP系统中应用了这一功能的企业却是寥寥无几。

这其中最重要的原因就在于预测功能的成功应用需要太多、太复杂的先决条件，而绝大多数企业根本不具备这些先决条件。换句话说，极少有企业能将预测过程中出现的种种复杂与深奥的参数进行量化与固化。

在预测功能的应用当中，最为核心的部分就是物料需求的推算规则。系统之所以能够依据物料的历史消耗数据推算出物料的未来需求值，靠的就是有一个明 确的推算规则。

我们需要事先将推算规则赋予给系统，系统才能够在这个规则的基础上依据物料的历史消耗值进行计算。

通常而言，我们将这个用于进行预测计算的 规则称之为预测模型（Forecast Model），而将这个模型中所量化的计算方法称之为预测公式（Forecast Formula）。

因此，物料的历史消耗数据仅仅是预测运算的变量，而预测模型与预测公式则在预测功能的应用中占据了最为核心的位置。选择一个合适的预测模型是成功应用预测 功能的必要条件。

因为如果模型选得不得当，再丰富的物料历史消耗数据都是没有意义的。而如果我们想要选择好正确的预测模型，就必须要事先对每个预测模型的 运算原理、以及预测模型中每个参数所起到的作用有着充分的了解。

这就让人很为难了，如果是研究此的专家学者，应用丰富的数学知识，或许能窥探一二；而模型这种东西都是建立在比较深的数学原理的总结之上的；一般人需要比较丰富的数学背景以及应用背景才能找出切合实际的方案；

所以说预测这个功能是美丽的，现实却是残酷的；

我们先来认识一下SAP预测功能里的主要一些概念；

SAP系统所提供的各种预测模型主要包括：

1：移动平均模型–Moving Average Model

2：加权移动平均模型–Weighted Moving Average Model

3：一阶指数平滑模型（含季节因子）-- First-Order Exponential Smoothing Model

3.1：常数模型–Constant Model

3.2：通用一阶指数平滑模型（含季节因子）-- General First-Order Exponential Smoothing Model

4：二阶指数平滑模型 – Second-Order Exponential Smoothing Model

SAP系统所提供的五大预测值评估标准，它们是：

1：误差总量–Error Total

2：初始化预测平均绝对偏差（MAD I）–Mean Absolute Deviation for Forecast Initialization

3：事后预测平均绝对偏差（MAD II）–Mean Absolute Deviation for Ex-Post Forecast

4：跟踪信号–Tracking Signal

5：泰尔系数–Theil Coefficient

SAP系统所提供的预测值修正方法–公差巷（Tolerance Lane）

预测模型中涉及到的五大参数，它们分别是：

1：α – alpha （基本平滑因子）

2：β – beta （趋势平滑因子）

3：γ – gamma （季节平滑因子）

4：δ – delta （平均绝对偏差因子）

5：σ – sigma （异常控制因子）

到此，我们言归正传，讨论预测模型；

对于常量需求形式（Constant requirements pattern）：

如果手工分析到过去消耗的数据代表着一个常量消耗流，我们就可以选择常量模型或使用平滑因子的常量模型。

这两个模型中的预测计算采用的是“first-order exponential smoothing”一阶指数平滑方法。当采用平滑参数的时，系统计算不同的参数组合，就是尝试不同的α因子值，并选择最优的参数组合，这种组合具备最低的平均绝对值偏差MAD（lowest mean absolute deviation）。

如果过去消耗表现出常量方式的时候，还有另外两个可能性，就是移动平均模型或带权重的移动平均模型。

在权重移动平均模型中，可以通过设定权重对于单个的过去消耗值，这可以使得系统将不按照平等方式来计算预测值，而是加入权重一起评估，这样我们就可以将近期消耗的值多给点权重，使得其扮演更重要的角色，这个类似一指数平滑情况。

移动平均模型（moving average model）的计算公式：

移动平均模型被用于排除在时间序列计算方式上的错误。其计算N个过去时间序列值的平均值。计算N个值的平均值是这样计算的，如（1）；

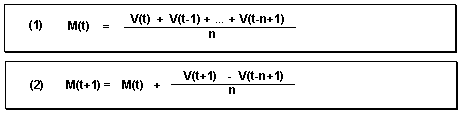
M（t）：第t+1个期间的预测值；

V（t）：期间t的消耗值；也可以说成对当前t期间的实际需求；

n：表示计算过去参与预测的期间的个数。

这里注意下公式1有个错误就是V（t）应该没有，V（t-n+1）应该是V（t-n）。

公式2的M（t+1）应该是M（t+2），V（t-n+1）应该是V（t-n）；公式2其实就是计算t+2期间的预测值，就是将公式1带入进去后就能看懂了。

还有就是如果你用过去n个期间的消耗值去预测未来n个期间，则除了n+1个期间是按照公式计算出来的，后面的期间的值都是同n+1的值一样的这个是固定的。

从公式1可以看出，计算t+1期间的预测就是通过对设定的过去n个期间的实际消耗值进行算术平均得到，不过，t+1期间的平均值（预测值）就是通过上一个期间的平均值，加上t+1期间的消耗值于n期间上的消耗值的差，除以n，也就是说，这个模型适用于从时间序列上来看是一个常量的情况，没有趋势没有季节，所有的历史数据都使用了权重因子1/n。

此模型适用环境：

1. 消耗值的波动比较平稳，无明显的上下起伏；

2. 消耗值的波动既无明显的趋势特征，也无明显的季节特征；

3. 各个消耗值所对应的历史期间在预测模型中具备相同的权重。

带权重移动平均模型（weighted moving average model）的计算公式：

公式（3）就是移动平均模型，其实就是使用的是相同权限的权限因子1/n的预测计算公式，（4）就是人工给出了每个权限因子的预测计算公式，其实就是加权平均数公式。

带权重的计算方式就是先分配一个权重组，里面包含了过去每个值的权重因子，所有权重因子的和是1。

这样每个过去值都会乘上这个权后后在进行平均值计算的。如果消耗趋势有点趋势性，就可以使用这个模型得到更好的效果。

由于权重的存在，可以给离现在最近的消耗值以大权重，不过这个模型十分依赖于给定的权重，所以要经常调整权重因子。

这里穿插一下关于移动平均法的概念介绍：（以便方便小伙伴们理解）

移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。

移动平均法适用于即期预测。

当产品需求既不快速增长也不快速下降，且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，是非常有用的。

移动平均法根据预测时使用的各元素的权重不同 

移动平均法是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。

因此，当时间序列的数值由于受周期变动和随机波动的影响，起伏较大，不易显示出事件的发展趋势时，使用移动平均法可以消除这些因素的影响，显示出事件的发展方向与趋势（即趋势线），然后依趋势线分析预测序列的长期趋势。 

移动平均法的种类：

移动平均法可以分为：简单移动平均和加权移动平均

一、简单移动平均法 
简单移动平均的各元素的权重都相等。简单的移动平均的计算公式如下： Ft=(At-1+At-2+At-3+…+At-n)/n式中， 
•	Ft--对下一期的预测值； 
•	n--移动平均的时期个数； 
•	At-1--前期实际值； 
•	At-2,At-3和At-n分别表示前两期、前三期直至前n期的实际值。 

二、加权移动平均法 
加权移动平均给固定跨越期限内的每个变量值以不同的权重。其原理是：历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。
除了以n为周期的周期性变化外，远离目标期的变量值的影响力相对较低，故应给予较低的权重。 加权移动平均法的计算公式如下： 

　　Ft=w1At-1+w2At-2+w3At-3+…+wnAt-n式中， 
•	w1--第t-1期实际销售额的权重； 
•	w2--第t-2期实际销售额的权重； 
•	wn--第t-n期实际销售额的权 
•	n--预测的时期数；w1+ w2+…+ wn=1 

常量模型中的一阶指数平滑（first-order exponential smoothing）的计算公式：

一阶指数平滑的原则是；越老的时间序列上的值，对于计算预测来说越不重要；当前预测的错误被带入随后预测执行中。

The older the time series values, the less important they become for the calculation of the forecast.

The present forecast error is taken into account for the following forecasts.

指数平滑法是布朗(Robert G…Brown)所提出，布朗(Robert G…Brown)认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续到最近的未来，所以将较大的权数放在最近的资料。

指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测，所有预测方法中，指数平滑是用得最多的一种。

简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；

而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。

也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。

所以说一阶指数平滑法预测t+1期间的话，只考虑t期间的实际消耗值，和t-1期间的平滑值S（t-1）。

指数平滑法的基本公式是：

• St–时间t的平滑值；
• yt–时间t的实际值； 也就是消耗值
• S(t – 1)–时间t-1的平滑值；
• a–平滑常数，其取值范围为[0,1]；

这个公式仅仅是用来计算t期间的平滑值的。根据我们设定的平滑因子来计算。
由该公式可知：

1.St是yt和 S（t – 1）的加权算数平均数，随着a取值的大小变化，决定yt和 S(t – 1)对St的影响程度，当a取1时，St = yt；当a取0时，St = St − 1。

2.St具有逐期追溯性质，可探源至S(t − t + 1)为止，包括全部数据。其过程中，平滑常数以指数形式递减，故称之为指数平滑法。

指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1，远期实际值对本期平滑值影响程度的下降越迅速；平滑常数a越接近于 0，远期实际值对本期平滑值影响程度的下降越缓慢。

由此，当时间数列相对平稳时，可取较大的a；当时间数列波动较大时，应取较小的a，以不忽略远期实际值的影响。生产预测中，平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。

3.尽管St包含有全期数据的影响，但实际计算时，仅需要两个数值，即yt和 S（t – 1），再加上一个常数a，这就使指数滑动平均具逐期递推性质，从而给预测带来了极大的方便。

4.根据公式

当欲用指数平滑法时才开始收集数据，则不存在y0。无从产生S0，自然无法据指数平滑公式求出S1，指数平滑法定义S1为初始值。

初始值的确定也是指数平滑过程的一个重要条件。

如果能够找到y1以前的历史资料，那么，初始值S1的确定是不成问题的。数据较少时可用全期平均、移动平均法；

数据较多时，可用最小二乘法。但不能使用指数平滑法本身确定初始值，因为数据必会枯竭。

如果仅有从y1开始的数据，那么确定初始值的方法有：

1）取S1等于y1；

2）待积累若干数据后，取S1等于前面若干数据的简单算术平均数，如：S1=（y1+ y2+y3）/3等等。

所以说SAP在进行预测前也是先要确定一个初始值的，也就有了初始化的说法，SAP的自动初始化采用的是取预测期间的最早一个期间的消耗值作为S1，也就是S1=Y1。

指数平滑的预测公式

据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。

一次指数平滑预测；当时间数列无明显的趋势变化，可用一次指数平滑预测。其预测公式为：

y（t+1）’=ayt+(1-a)yt’

式中：

y（t+1）’：t+1期的预测值，即本期（t期）的平滑值St ；
yt：t期的实际值；
yt’：t期的预测值，即上期的平滑值S（t-1）

该公式又可以写作：y（t+1）’=yt’+a(yt- yt’)。可见，下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。

公式是：


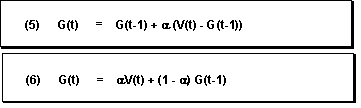
公式5就是计算公式，公式6是5的转换形式。系统会计算出一个基本值，其实这个值就是预测值，不过如果这个值有小数，则会被向上取整。

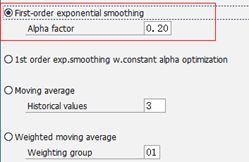
1.如果观察值的长期趋势变动接近稳定的常数，应取居中阿尔法值(一般取0.6—0.4)使观察值在指数平滑中具有大小接近的权数；

2.如果观察值呈现明显的季节性变动时，则宜取较大的阿尔法值(一般取0.6一0.9)，使近期观察在指数平滑值中具有较大作用，从而使近期观察值能迅速反映在未来的预测值中；

3.如果观察值的长期趋势变动较缓慢，则宜取较小的α值(一般取0.1—0.4)，使远期观察值的特征也能反映在指数平滑值中。

在确定预测值时，还应加以修正，在指数平滑值S，的基础上再加一个趋势值β，因而，原来指数平滑公式也应加一个b。

如何快速根据消耗的变化来进行预测，主要取决于我们提供的平滑因子α。如果设置α=0，则t+1期间的预测值就是t-1期间的平滑值，也就是说预测将不会根据t期间的消耗值来做出反应变化。

如果α=1，则预测值就是t期间的实际消耗值，预测做出迅速反应。但我们通常不会取两个极端，总是双方都互相参考来进行预测。

SAP系统认为一般来说α设定在0.1到0.5之间比较合适。

常量模型中使用调整因子的一阶指数平滑（first-order exponential smoothing）的计算公式：
SAP里在一阶平滑方法里改良出了，带调整因子的方法，其主要原理就是系统自动计算不同的平滑因子参数α的组合，来计算出很多组的平滑值，然后每组计算出一个MAD，系统选择最小的MAD来进行预测。

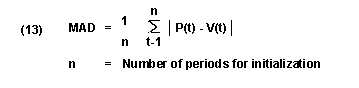
MAD就是每组期间中的每个t期间的预测值减去实际消耗值的绝对值，然后求和，后除以设置的期间数量。

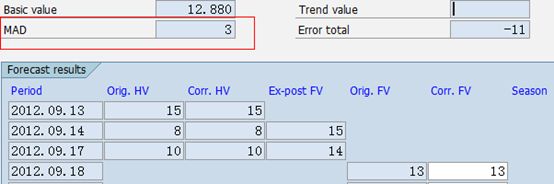
如上图，MAD的计算过程距离如下，三个过去期间的实际消耗值分别是15/8/10，可以先计算出每个过去期间的平滑之St。

15/13.6/12.88，15这个值由于是S1所以系统直接取第一个期间的实际值。由于n=3，所以计算MAD=（|15-15|+|13.6-8|+|12.88-10|）/3=2.82取整就是3；

这里简单为小伙伴们附带提一下趋势预测模型（Trend Model）的相关内容；

如果过去消耗的数据表现出一种趋势性，那么预测的时候选择趋势模型或二阶指数平滑模型（second-order exponential smoothing model），对应系统的模型选择是T/O/B。

在趋势模型中，系统依靠一阶指数平滑程序来计算预测值。在二阶指数平滑模型中，可以在使用或不使用参数优化的条件中进行选择。

T Trend model

O 2nd order trend with adjustment of smoothing factor

B 2nd order trend

下面的公式是集成了使用一阶指数平滑的趋势模型和季节模型一起的公式。



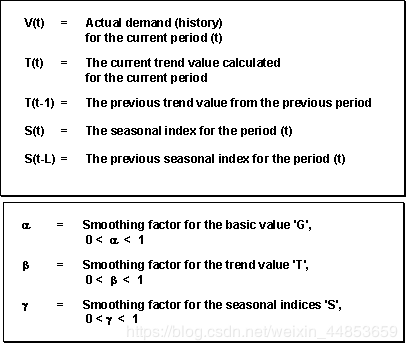
公式7就是一阶指数平滑趋势和季节模型的总预测公式；

i表示从当前t期间向未来的第i个期间（t+i），P（t+i）表示预测未来t+i期间的值。

和公式7相关的是，t期间的预测值也可以说成是基本值，也可以说成是平滑值G(t)；

T(t)趋势值t期间的趋势值；

当使用趋势模型的时候公式后面的S（t）=1，γ=0。

所以公式7就变成了：

P(t+i)=G(t)+i*T(t)；意思就是趋势预测的值，就是在t期间的预测的预测值或者叫平滑值，加上趋势值。

从公式8看出，G(t)也就是t期间的预测值，也可以说是t期间的基本值或平滑值，由于S(t)=1，然后得到的公式是G(t)：

G(t-1)+T(t-1)+α(V(t)-G(t-1)-T(t-1))

转换公式，合并同类项后得到：αV(t)+(1-α)G(t-1)+(1-α)T(t-1)

其实一看就知道G（t）的值就是t的预测值加上t-1期间的趋势值。公式9就是求t期间的趋势值的；

变形后得到：（1-β）T（t-1）+β（G（t）-G（t-1））

也就是说t期间的平滑值减去t-1期间的平滑值。

以上为本章全部内容，希望对小伙伴们有所帮助；