ArcFace 与 人脸识别三要素

ArcFace

CosFace, AM-Softmax

SphereFace

近年来，卷积神经网络由于在学习辨别特征方面的优势而显着提高了人脸识别的性能。为了增强 Softmax 损失的判别能力，乘性角度余量(SphereFace)和加性余弦余量(AM-Softmax, CosFace)分别将角度余量和余弦余量加入到损失函数中。
ArcFace 提出了一种新的监督信号，即加性角度裕度(ArcFace)，它具有比已有监督信号更好的几何解释。具体而言， ArcFace $\cos (\theta +m)$ 基于 L2标准化权重和特征，直接最大化角（弧）空间中的决策边界。与乘法角度裕度 $\cos (m\theta )$ 和加性余弦余量 $\cos \theta -m$ 相比，ArcFace 可以获得更具辨别力的深度特征。
ArcFace 在 MegaFace 挑战赛中获得了最领先的表现，并公开提供数据、模型和训练/测试代码。文章实验充分，主要为以下5组：

• 基于 LResNet34E-IR 网络和精炼的 MS1M 数据集，分析训练期间 SphereFace、CosineFace 和 ArcFace 的目标 logit 曲线和 $\theta$ 分布。
• 以 Softmax 作为损失函数在 VGG2 数据集上训练，并通过 LFW、CFP 和 AgeDB 评估不同的网络设置性能。
• 基于 SE-LResNet50E-IR 网络和 ArcFace 损失在 VGG2 数据集上训练，探索权重衰减(WD)值在 LFW、CFP 和 AgeDB 上对验证性能的影响。
• 基于 LMobileNetE 网络和 ArcFace 损失在精炼的 MS1M 数据集上训练模型，搜索最佳角度边距。
• 使用 LResNet100E-IR 网络在精炼的 MS1M 数据集上训练以参加 MegaFace 挑战。

基于深度卷积网络嵌入的人脸识别

人脸验证、人脸聚类和人脸识别的最先进方法是借助深度卷积网络嵌入的人脸表示(DeepFace, FaceNet, Deep Face Recognition)。通常在姿态归一化步骤之后，深度卷积网络负责将人脸图像映射到嵌入特征向量中，使得同一人的特征具有较小的距离，而不同个体的特征具有较大的距离。

基于深度卷积网络嵌入的各种人脸识别方法主要在以下三个方面有所不同：

训练数据

公共可用训练数据，例如 VGG-Face、VGG2-Face、CAISA-WebFace、UMDFaces，MS-Celeb-1M 和 MegaFace，身份数量范围从几千到五十万。虽然 MS-Celeb-1M 和 MegaFace 个体数量大，但它们会受到注释噪声和长尾分布的影响。相比之下，Google 的私有训练数据身份数量高达有数百万。从人脸识别供应商测试(FRVT)的最新业绩报告中来看，中国创业公司依图借助其私有的18亿张人脸图像排名第一。由于训练数据数量级上的差异，工业界的人脸识别模型比学术界的模型表现更好。训练数据的差异也使得一些深度人脸识别结果不能完全重现。

网络结构和设置

高容量深度卷积网络，例如 ResNet[14, 15, CenterLoss, RangeLoss, SphereFace]和 Inception-ResNet[3]，较之 VGG 网络[31]和 Google InceptionV1 网络(FaceNet)可以获得更好的性能。不同的深度人脸识别应用倾向于速度和准确度之间的不同权衡(MobileNets, ShuffleNet)。 对于移动设备上的人脸验证，实时级运行速度和紧凑的模型尺寸对于流畅的客户体验至关重要。而对于十亿级安全系统，高精度与效率同等重要。

损失函数的设计

(1) 基于欧几里德边界的损失。
在 DeepFace 和 Deep Face Recognition 中，通过一组已知身份训练 Softmax 分类层。然后从网络的中间层获取特征向量，并用于泛化到训练个体之外的识别。Center Loss、Range Loss 和 Marginal Loss 增加额外的惩罚来压缩内部方差或扩大类间距离以提高识别率，但所有这些仍然结合 Softmax 训练识别模型。然而，当身份数量增加到百万级别时，基于分类的方法(DeepFace, Deep Face Recognition)其分类层会消耗大量 GPU 内存，并且更适于每个身份平衡且足量的训练数据。

Contrastive Loss 和 Triplet Loss 利用配对训练策略。Contrastive Loss 函数由正对和负对组成。损失函数的梯度将正对聚到一起并将负对推开。Triplet Loss 最小化锚和正样本之间的距离，并使锚与来自不同身份的负样本之间的距离最大化。然而，由于需要选择有效训练样本，Contrastive Loss 和 Triplet Loss 的训练过程很棘手。

(2) 基于角和余弦边界的损失。

L-Softmax 提出大边界 Softmax ，通过向每个身份添加乘性角度约束来以改善特征辨别。SphereFace $\cos (m\theta )$ 将 L-Softmax 中的权重归一化。由于余弦函数的非单调性， SphereFace 应用分段函数以保证单调。SphereFace 在训练期间结合 Softmax 损失，以加快和确保收敛。为了克服 SphereFace 的优化难题，加性余弦余量(AM-Softmax, CosFace) $\cos (\theta )-m$ 将角度边界移至余弦空间。加性余弦余量的实现和优化比 SphereFace 容易得多。加法余弦余量很容易复现，并在 MegaFace(TencentAILab_FaceCNN_v1)上实现了最领先的性能。与基于欧几里得边界的损失相比，基于角和余弦边界的损失显式增加了对超球流形的判别约束，其本质上匹配了人脸位于流形上的先验条件。

ArcFace 的改进

上述三个属性：数据、网络和损失，对人脸识别模型性能的影响依次递减。ArcFace 亦从这三个方面上进行改进。

数据
ArcFace 训练前以自动和手动的方式完善了最大的公共可用训练数据 MS-Celeb-1M。其使用 Resnet-27[14, RangeLoss, MarginalLoss ]网络和以及 NIST 人脸识别奖挑战赛中的 Marginal Loss 检查了精制 MS1M 数据集的质量。发现 MegaFace 100万个干扰物与 FaceScrub 数据集之间存在数百个重叠人脸图像，这显着影响评估结果。于是手动从 MegaFace 干扰物中找到这些重叠人脸图像。
网络
以 VGG2 作为训练数据，论文对卷积网络配置进行了广泛的对比实验，并报告了 LFW、CFP和 AgeDB 的验证准确率。ArcFace 所提出的网络设置在大姿态和年龄变化下仍具有鲁棒性。同时还探讨了在速度和准确性之间的权衡。

损失
如下图所示，基于 L2归一化权重和特征，ArcFace 损失函数 $\cos (\theta +m)$ 直接最大化角（弧）空间中的决策边界。 ArcFace 优于基线方法，例如乘性角度余量(SphereFace)和加性余弦余量(AM-Softmax, CosFace)。论文从半难样本分布的角度解释了为什么 ArcFace 优于 Softmax、SphereFace 和 CosineFace(AM-Softmax, CosFace)。

从 Softmax 到 ArcFace

Softmax

使用最广的分类损失函数，Softmax损失为：
$$L_1=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{W_{y_i}^T{x}_i+b_{y_i}}}{{\sum }_{j=1}^n{e}^{W_j^T{x}_i+b_j}},$$
其中 $x_i\in {\mathbb{R}}^d$ 表示第 $i$ 个样本的深度特征，属于第 $y_i$ 类。依照 Center Loss、Range Loss、SphereFace 和 CosFace，在论文中将特征维度 $d$ 设置为 $512$。$W_j\in {\mathbb{R}}^d$ 表示最后一个全连接层权重 $W\in {\mathbb{R}}^{d\times n}$ 的第 $j$ 列而 $b\in {\mathbb{R}}^n$ 是偏置。批量大小和类别数分别为 $m$ 和 $n$。
传统的 Softmax 损失在深层人脸识别中应用广泛(Deep Face Recognition, VGGFace2)。然而，Softmax 损失函数没有明确地优化特征以使正对的相似性得分更高并且负对的相似性得分更低，这导致性能差距。

权重归一化

为简单起见，ArcFace 像 SphereFace 中一样固定偏置 $b_j=0$。然后转换目标 logit[32]如下：
$$W_j^T{x}_i=\Vert W_j\Vert \Vert x_i\Vert \cos {\theta }_j,$$

遵从 SphereFace、CosFace 和 NormFace，文中通过 L2归一化固定 $\Vert W_j\Vert =1$，这使得预测仅取决于特征向量和权重之间的角度。
$$L_2=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{\Vert x_i\Vert \cos ({\theta }_{y_i})}}{e^{\Vert x_i\Vert \cos ({\theta }_{y_i})}+{\sum }_{j=1,j̸=y_i}^n{e}^{\Vert x_i\Vert \cos {\theta }_j}}$$

在 SphereFace 的实验中，L2权重归一化对性能的提高甚微。

乘性角度余量

在 SphereFace 中，通过角度乘法引入角度边界距离 $m$。
$$L_3=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{\Vert x_i\Vert \cos (m{\theta }_{y_i})}}{e^{\Vert x_i\Vert \cos (m{\theta }_{y_i})}+{\sum }_{j=1,j̸=y_i}^n{e}^{\Vert x_i\Vert \cos {\theta }_j}},$$

其中 ${\theta }_{y_i}\in \left[0,\pi /m\right]$。为了消除这一约束，$\cos (m{\theta }_{y_i})$ 由分段单调函数 $\psi ({\theta }_{y_i})$代替。SphereFace 表示为：
$$L_4=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{\Vert x_i\Vert \psi ({\theta }_{y_i})}}{e^{\Vert x_i\Vert \psi ({\theta }_{y_i})}+{\sum }_{j=1,j̸=y_i}^n{e}^{\Vert x_i\Vert \cos {\theta }_j}},$$

其中 $\psi ({\theta }_{y_i})=(-1{)}^k\cos (m{\theta }_{y_i})-2k$，${\theta }_{y_i}\in \left[\frac{k\pi }{m},\frac{(k+1)\pi }{m}\right]$，$k\in \left[0,m-1\right]$，$m⩾1$ 是控制角度边距的大小的整数。然而， SphereFace 的实现中整合了 Softmax 监督以保证训练的收敛，并且权重由动态超参数 $\lambda$ 控制。加入额外的 Softmax 损失，$\psi ({\theta }_{y_i})$ 实际上是：
$$\psi ({\theta }_{y_i})=\frac{(-1{)}^k\cos (m{\theta }_{y_i})-2k+\lambda \cos ({\theta }_{y_i})}{1+\lambda }$$

其中 $\lambda$ 是一个额外的超参数，以利于 SphereFace 的训练。$\lambda$ 在开始时设置为1,000，并且减少到5以使每个类的角度空间更紧凑。这个额外的动态超参数 $\lambda$ 使得 SphereFace 的训练相对棘手。

特征归一化

特征归一化在人脸验证中应用广泛，例如 L2归一化欧几里德距离和余弦距离[29]。Parde 等人[30]观察到使用 Softmax 损失学习的特征的 L2范数可以提供人脸质量的信息。优质正面的特征具有高 L2范数，而具有极端姿态的模糊人脸有低 L2范数。L2-Softmax 将 L2约束添加到特征描述符，并将特征限制在固定半径的超球面上。使用现有的深度学习框架可以非常方便地实现对特征的 L2规范化，并显着提高人脸验证的性能。AM-Softmax 中指出，当低质量人脸图像的特征范数非常小时，梯度范数可能会非常大，这可能会增加梯度爆炸的风险。在 [25]，COCO Loss，TencentAILab FaceCNN v1 和 NormFace 中也指出了 特征归一化的优点，并且从分析、几何及实验角度解释了特征规范化。

正如我们从上面的工作中可以看到的，对特征和权重的 L2归一化是超球面度量学习的重要步骤。特征和权重归一化背后的直观洞察是消除径向变化并推动每个特征分布在超球面流形上。

与 L2-Softmax、CosFace、NormFace 和 AM-Softmax 的做法相同，我们通过 L2规范化固定 $\Vert x_i\Vert$ 并重新缩放 $\Vert x_i\Vert$ 到 $s$，这是超球半径，其下限在 L2-Softmax 中给出。本文实验中使用 $s=64$ 进行人脸识别(L2-Softmax, CosFace)。 基于特征和权重归一化，我们可以得到 $W_j^T{x}_i=\cos {\theta }_j$。

如果将特征规范化应用于 SphereFace，我们可以获得特征规范化的 SphereFace，表示为 SphereFace-FNorm：
$$L_5=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{s\psi ({\theta }_{y_i})}}{e^{s\psi ({\theta }_{y_i})}+{\sum }_{j=1,j̸=y_i}^n{e}^{s\cos {\theta }_j}}$$

附加余弦余量

在 AM-Softmax 和 CosFace 中，将角度边距 $m$移至 $\cos \theta$ 的外部，因此他们提出了余弦边界损失函数：
$$L_6=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{s(\cos ({\theta }_{y_i})-m)}}{e^{s(\cos ({\theta }_{y_i})-m)}+{\sum }_{j=1,j̸=y_i}^n{e}^{s\cos {\theta }_j}}.$$

本文将余弦余量 $m$ 设置为 $0.35$(AM-Softmax, CosFace)。与 SphereFace 相比，附加余弦余量（CosineFace）有三个优点：

• 非常容易实现，没有棘手的超参数;
• 没有 Softmax 监督，更清晰，更易收敛;
• 性能有明显改善。

附加角度边距

尽管 AM-Softmax 和 CosFace 中的余弦余量具有从余弦空间到角度空间的一对一映射，但这两个边距之间仍然存在差异。事实上，与余弦边界相比，角度边界具有更清晰的几何解释，并且角度空间中的边距对应于超球面流形上的弧距。

我们在 $\cos \theta$ 中添加一个角度余量 $m$。由于 $\cos (\theta +m)$ 低于 $\cos (\theta )$，当 $\theta \in \left[0,\pi -m\right]$ 时，约束对于分类更严格。所提 ArcFace 定义为：
$$L_7=-\frac{1}{m}\sum _{i=1}^m\log \frac{e^{s(\cos ({\theta }_{y_i}+m))}}{e^{s(\cos ({\theta }_{y_i}+m))}+{\sum }_{j=1,j̸=y_i}^n{e}^{s\cos {\theta }_j}},$$

约束条件：
$$W_j=\frac{W_j}{\Vert W_j\Vert },x_i=\frac{x_i}{\Vert x_i\Vert },\cos {\theta }_j=W_j^T{x}_i.$$

如果对提出的附加角度余量 $\cos (\theta +m)$ 展开，可以得到 $\cos (\theta +m)=\cos \theta \cos m-\sin \theta \sin m$。 与 AM-Softmax 和 CosFace 中提出的附加余弦余量 $\cos (\theta )-m$ 相比，ArcFace 二者类似，但由于 $\sin \theta$，边界距离是动态的。

图2 .说明了 ArcFace，及弧边距所对应的角度边距。与 SphereFace 和 CosFace 相比，ArcFace 具有最佳的几何解释。

图2 . ArcFace 的几何解释。不同的颜色区域表示来自不同类的特征空间。ArcFace 不仅可以压缩特征区域，还可以对应超球面上的测地距离。

二元案例下的比较

为了更好地理解从 Softmax 到所提 ArcFace 的过程，论文在表Table 1 和图3. 中给出了二元分类情况下的决策边界。基于权重和特征归一化，这些方法的主要区别在于我们放置的边界距离。


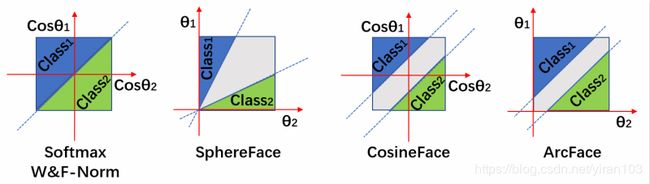
图3. 二元分类情形下不同损失函数的决策余量。虚线表示决策边界，灰色区域是决策余量。

目标 Logit 分析

为了研究为什么 SphereFace、CosineFace 和 ArcFace 可以改善人脸识别性能，我们在训练期间分析目标 logit 曲线和 $\theta$ 分布。 在这里，我们使用 LResNet34E-IR 网络和精炼的 MS1M 数据集。

在图4(a)中，我们绘制了Softmax、SphereFace、CosineFace 和 ArcFace 的目标 logit 曲线。对于 SphereFace，最佳设置是 $m=4$ 和 $\lambda =5$，这类似于 $m=1.5$ 和 $\lambda =0$ 的曲线。但是，SphereFace 的实现要求 $m$ 为整数。当我们尝试最小乘性余量，$m=2$ 和 $\lambda =0$ 时，训练无法收敛。 因此，从 Softmax 稍微降低目标 logit 曲线能够增加训练难度并改善性能，但是减少太多可能导致训练发散。

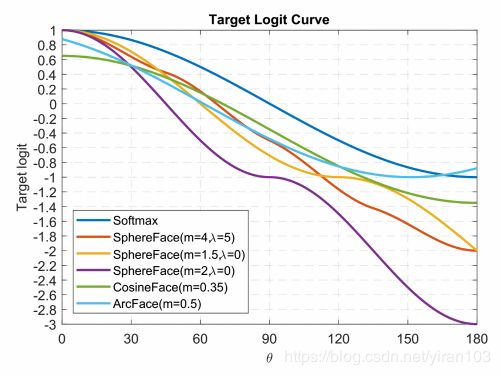
图4(a) 目标 logit 曲线

CosineFace 和 ArcFace 都遵循这一见解。从图4(a) 可以看出，CosineFace 沿 y 轴的负方向移动目标 logit 曲线，而 ArcFace 沿 x 轴的负方向移动目标 logit 曲线。现在，我们可以轻松了解从 Softmax 到 CosineFace 和 ArcFace 的性能改进。

对于边距为 $m=0.5$ 的 ArcFace，当 $\theta \in \left[0,180^{\circ }\right]$ 时，目标 logit 曲线不会单调递减。实际上，当 $\theta >151.35^{\circ }$ 时，目标 logit 曲线会上升。但是，如图4(c )所示，$\theta$ 是一个中心位于 $90^{\circ }$ 的高斯分布，且当随机初始化网络时最大角度低于$105^{\circ }$。在训练期间几乎从未达到 ArcFace 的递增区间。因此不需要明确地处理这个问题。

图4(c ) 训练期间的 $\theta$ 分布

在图4(c )中，我们展示了CosineFace 和 ArcFace 在训练的三个阶段中（例如开始、中间和结束） $\theta$ 的分布。分布中心逐渐从 $90^{\circ }$ 移至 $35^{\circ }-40^{\circ }$。在图4(a)中，我们发现在 $30^{\circ }$ 到 $90^{\circ }$ 的区间上， ArcFace 的目标 logit 曲线低于 CosineFace 的目标logit曲线。因此，与 CosineFace 相比，ArcFace 在此区间内会产生更严格的边际惩罚。在图4(b) 中，我们展示了 Softmax、CosineFace 和 ArcFace 在训练批次上估计的目标 logit 收敛曲线。我们还可以发现开始时， ArcFace 的边界惩罚比 CosineFace 重，因为红色虚线低于蓝色虚线。在训练结束时，ArcFace 收敛的比 CosineFace 好，因为 $\theta$ 的直方图在左边（图4(c )），目标 logit 收敛曲线更高（图4(b) ）。从图4(c )，我们可以发现在训练结束时几乎所有 $\theta$ 都小于 $60^{\circ }$。超出此区域的样本是最难的样本或训练数据集的噪声样本。尽管 CosineFace 在 $\theta <30^{\circ }$（图4(a)）时会给予更严格的边界惩罚，但即使在训练结束时也很少达到这个范围（图4(c )）。因此，我们也可以理解为什么在本节中 SphereFace 即使设置相对较小的余量也能获得非常好的性能。

图4(b) 目标 logit 收敛曲线

总之，当 $\theta \in \left[60^{\circ },90^{\circ }\right]$ 时，添加太多的边界惩罚可能导致训练发散，例如 SphereFace（$m=2$ 和 $\lambda =0$）。当 $\theta \in \left[30^{\circ },60^{\circ }\right]$ 时增加边界距离可以提高性能，因为这部分对应的是最有效的半难负样本[FaceNet]。 当 $\theta <30^{\circ }$ 时增加边界距离无法明显改善性能，因为此部分对应于最简单的样本。当我们回顾图4(a) 并对 $\left[30^{\circ },60^{\circ }\right]$ 之间的曲线进行排序时，我们可以理解为什么在各自最佳参数设置下，性能可以从 Softmax、SphereFace、CosineFace 到 ArcFace 逐步提升。请注意，这里 $30^{\circ }$ 和 $60^{\circ }$ 是简单和难训练样本的粗略估计阈值。

实验数据

训练数据

我们使用两个数据集，VGG2 和 MS-Celeb-1M 作为训练数据。

VGG2
VGG2 数据集包含一个具有8,631个身份（3,141,890个图像）的训练集和一个具有500个身份（169,396个图像）的测试集。VGG2 在姿态、年龄、光照、种族和职业方面有很大差异。由于 VGG2 是一个高质量的数据集，我们直接使用它而不进行数据细化。

MS-Celeb-1M
最初的 MS-Celeb-1M 数据集包含大约10万个身份的1000万张图像。为了降低 MS-Celeb-1M 的噪音并获得高质量的训练数据，我们按照与身份中心的距离对每个身份的所有人脸图像进行排序。

• 对于每个身份，自动删除特征向量距离身份的特征中心太远的人脸图像(Marginal Loss)。
• 接着手动检查每个身份在第一个自动步骤中阈值周围的人脸图像。

最终得到一个包含了85,000个身份的380万张人脸图像数据集。为了方便其他研究人员重现本文中的所有实验，我们将精制的 MS1M 数据集公开在二进制文件中，但请在使用此数据集时引用原始论文并遵循原始许可证。我们在这里的贡献只是训练数据细化，而不是发布。

验证数据

我们采用自然环境下的标记人脸(LFW)、名人正剖面(CFP) 和年龄数据库(AgeDB)作为验证数据集。

LFW
LFW 数据集包含 $13,233$ 张来自 $5749$ 个不同身份的网络收集图像，其姿势、表情和照明有很大差异。遵循 unrestricted with labelled outside data 的标准协议，我们提供 $6,000$ 对人脸的验证准确性。

CFP
CFP 数据集由500个科目组成，每个科目有10个正面图像和4个档案图像。评估协议包括正面-正面(FF)和正面-档案(FP)人脸验证，每个人脸验证具有10个文件夹，其具有350个同一人对和350个不同人对。在本文中，我们仅使用最具挑战性的子集 CFP-FP 来报告性能。

AgeDB
AgeDB 数据集是一个自然环境数据集，在姿势、表情、光照和年龄方面有很大变化。AgeDB 包含 $440$ 个独立科目的 $12,240$ 张图片，如演员、女演员、作家、科学家和政治家。每个图像都根据身份、年龄和性别属性进行注释。最低和最高年龄分别为 $3$ 岁和 $101$ 岁。每个科目的平均年龄范围是 $49$ 岁。有四组年龄差距不同的测试数据（分别为 $5$ 岁、$10$ 岁、$20$ 岁和 $30$ 岁）。每组有十个人脸图像分割，每个分组包含 $300$ 个正样本和 $300$ 个负样本。人脸验证评估指标与 LFW 相同。本文仅使用最具挑战性的子集 AgeDB-30 来报告性能。

测试数据

MegaFace
MegaFace 数据集作为最大的公共可用测试基准发布，旨在评估百万级干扰物下人脸识别算法的性能。MegaFace 数据集包括注册集和验证集。注册集是来自雅虎 Flickr 照片的一部分，由来自690k 个不同个体的超过一百万张图像组成。 验证集是两个现有的数据库：FaceScrub 和 FGNet。 FaceScrub 是一个公开可用的数据集，其中包含 $530$ 个不同个体的10万张照片，其中 $55,742$ 的图像是男性，$52,076$ 的图像是女性。 FGNet 是一个人脸老化数据集，有 $82$ 个身份的 $1002$ 张图像。每个身份都有不同年龄的多个人脸图像（从$1$到$69$）。

可以理解的是，收集 MegaFace 的数据非常艰巨且耗时，因此数据噪声是不可避免的。FaceScrub 数据集中来自一个特定身份的所有人脸图像应属于同一人。对于100万个干扰者，不应该与 FaceScrub 身份重叠。然而，我们发现噪声人脸图像不仅存在于 FaceScrub 数据集中，而且还存在于一百万个干扰物中，这显着影响了性能。

我们根据与身份中心的余弦距离对所有人脸进行排序，手动清理 FaceScrub 数据集，最后找到 $605$ 个噪声的人脸图像。在测试期间，我们将噪声人脸改为另一个正确人脸，这可以将识别准确度提高约 $1\%$。在图fig：disnoise中，我们给出了来自 MegaFace 干扰器的噪声人脸图像示例。来自 MegaFace 干扰者的所有四张脸部图像都是亚历克·鲍德温。我们手动清理 MegaFace 干扰物，最后找到$707$个噪声人脸图像。在测试过程中，我们添加了一个额外的特征维度来区分这些噪声脸，这可以将识别精度提高大约 $15\%$。

即便七位对这些名人非常熟悉的注释者对嘈杂的人脸图像被进行了双重检查，我们仍然不能保证这些图像是 $100\%$ 无噪声的。我们将 FaceScrub 数据集和 MegaFace 干扰者的噪声列表放在网上。我们相信群众有敏锐的眼光，我们会根据其他研究人员的反馈更新这些清单。

网络设置

我们首先使用 VGG2 作为训练数据并将 Softmax 作为损失函数，根据不同的网络设置评估人脸验证性能。本文中的所有实验均由 MxNet 实现。 我们将批量大小设置为 $512$，并在四个或八个 NVIDIA Tesla P40(24GB) GPU 上训练模型。学习率从 $0.1$ 开始，在100k，140k，160k迭代中除以 $10$。总迭代步长设置为200k。 我们设定动量为 $0.9$，权重衰减为 $5e-4$（表Table 5）。

输入设置

与 Center Loss 和 SphereFace 中相同，我们使用五个关键点（眼睛中心、鼻尖和嘴角）进行相似性变换以标准化人脸图像(MTCNN)。 裁剪人脸并调整为 $112\times 112$，接着 RGB 图像中的每个像素（范围在$ [0,255] $之间）通过减去 $127.5$ 然后除以 $128$ 来归一化。

由于大多数卷积网络是为 ImageNet 分类任务而设计的，因此输入图像大小通常设置为 $224\times 224$ 或更大。然而，我们裁剪出的人脸仅有 $112\times 112$。为了保留更高的特征映射分辨率，我们在第一个卷积层使用 $conv3\times 3$ 和 $stride=1$，而非 $conv7\times 7$ 和 $stride=2$。 对于这两个设置，卷积网络的输出大小为 $7\times 7$（在网络名称前面表示为“L”）和 $3\times 3$。

输出设置

在最后几层中，可以研究一些不同的选项以检验嵌入设置如何影响模型性能。除 Option-A 之外的所有特征嵌入维度设置为 $512$，因为 Option-A 中的嵌入大小由最后一个卷积层的通道大小决定。

在测试期间，分数为两个特征向量的余弦距离。人脸识别和验证任务分别使用最近邻和阈值比较。

块设置

除了原始的 ResNet 单元外，我们还研究了一种更先进的残差单元设置，用于训练人脸识别模型。在图7 中，我们展示了改进的残差单元（在模型名称末尾表示为“IR”），它具有 BN-Conv-BN-PReLu-Conv-BN 结构。与 ResNet 提出的残差单元相比，我们为第二个卷积层而不是第一个卷积层设置了 $stride=2$。另外，用 PReLu 替换原来的 ReLu。

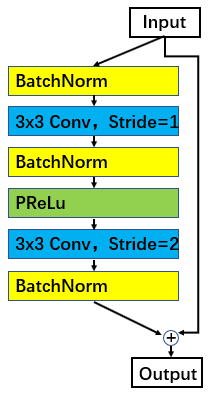
图7. 改进的残差单元：BN-Conv-BN-PReLu-Conv-BN

基础网络

基于模型结构设计的最新进展，我们还探索了将 MobileNet、Inception-Resnet-V2、DenseNet、SENet 和 DPN 用于深度人脸识别。本文从准确性、速度和模型大小方面比较了这些网络之间的差异。

网络设置结论

输入选择 L
在表Table 2中，我们比较了两个网络是否有“L”的设置。当使用 $conv3\times 3$ 和 $stride=1$ 作为第一个卷积层时，网络输出为 $7\times 7$。相比之下，如果我们使用 $conv7\times 7$ 和 $stride=2$ 作为第一个卷积层，网络输出仅有 $3\times 3$。从表Table 2可以明显看出，在训练期间选择较大的特征图可以获得更高的验证精度。

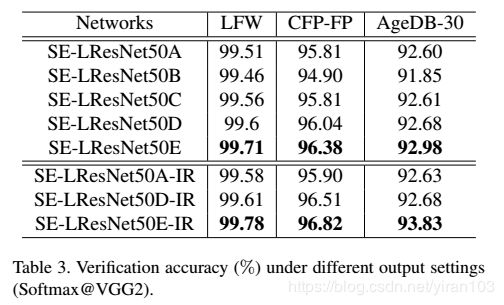
输出选择 E
在表Table 3中，我们给出了不同输出设置之间的详细比较。选项E(BN-Dropout-FC-BN)获得最佳性能。在本文中，dropout 参数设置为 $0.4$。Dropout 可以有效地充当正则化项，以避免过度拟合并获得更好的深度识别泛化。

Block 选择 IR
在表Table 4中，我们给出了原始剩余单元和改进的剩余单元之间的比较。 从结果可以看出，提出的 BN-Conv(stride=1)-BN-PReLu-Conv(stride=2)-BN 单元可以明显提高验证性能。

主干比较
在表Table 8中，我们给出了不同主干的验证准确性、测试速度和模型大小。运行时间在 P40 GPU 上估算。由于 LFW 的性能几乎已经饱和，我们重点在更具挑战性的测试集 CFP-FP 和 AgeDB-30 上比较这些网络骨干网。Inception-Resnet-V2 网络获得最佳性能，同时运行时间最长（$53.6ms$），模型最大（$642MB$）。相比之下，MobileNet 可以在 $4.2ms$ 内完成人脸特征嵌入抽取，模型为 $112MB$，性能仅略有下降。正如我们从表Table 8中看到的那样，这些大型网络（例如 ResNet-100、Inception-Resnet-V2、DenseNet、DPN 和 SE-Resnet-100）之间的性能差距相对较小。基于精度、速度和模型尺寸之间的权衡，我们选择 LResNet100E-IR 来进行 MegaFace 挑战的实验。

权重衰减

基于 SE-LResNet50E-IR 网络，我们还探讨了权重衰减(WD)值如何影响验证性能。从表Table 5可以看出，当权重衰减值设置为 $5e-4$ 时，验证精度达到最高点。因此，我们在所有其他实验中将重量衰减定为 $5e-4$。

损失设置

由于边界参数 $m$ 在 ArcFace 中起着重要作用，我们首先进行实验以搜索最佳角度边距。我们使用 LMobileNetE 网络和 ArcFace 损失在精炼的 MS1M 数据集上训练模型，并将
$m$ 从 $0.2$ 变到 $0.8$。如表Table 6所示，在所有数据集上的性能从 $m=0.2$ 处开始提升，并在 $m=0.5$ 时饱和。接着，验证准确度从 $m=0.5$ 减少。在本文中，我们将附加角度裕度 $m$ 固定为 $0.5$。

基于 LResNet100E-IR 网络和精炼的 MS1M 数据集，我们比较了不同损失函数的性能，例如 Softmax、SphereFace、CosineFace(AM-Softmax, CosFace) 和 ArcFace。在Table 7中，我们给出了 LFW、CFP-FP 和 AgeDB-30 数据集的详细验证准确性。由于 LFW 几乎饱和，性能改善并不明显。

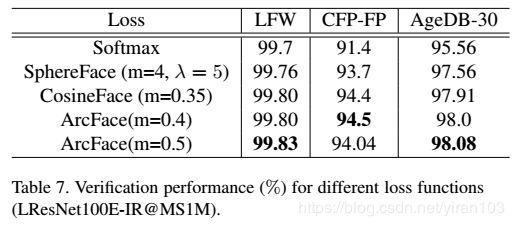
我们发现：

• 与 Softmax 相比，SphereFace、CosineFace 和 ArcFace 明显改善了性能，特别是在姿态和年龄变化较大的情况下。
• CosineFace 和 ArcFace 明显优于 SphereFace，实现起来更容易。无需 Softmax 的额外监督，CosineFace 和 ArcFace 都可以轻松收敛。相比之下，Softmax 的额外监督对于 SphereFace 在训练期间避免发散是必不可少的。
• ArcFace 略好于 CosineFace。然而，ArcFace 更加直观，并且在超球面流形上具有更清晰的几何解释。

MegaFace Challenge1 on FaceScrub

对于 MegaFace 挑战的实验，我们使用 LResNet100E-IR 网络和精炼的 MS1M 数据集作为训练数据。在表Table 9和Table 10中，我们在原始 MegaFace 数据集和精炼的 MegaFace 数据集上给出了识别和验证结果。


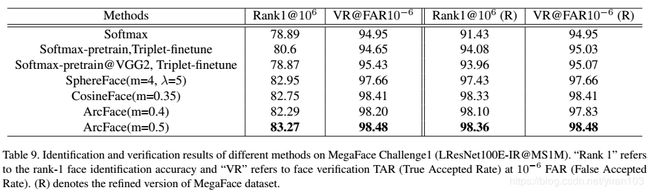
在表 Table 9中，我们使用整个精炼的 MS1M 数据集来训练模型。我们比较了所提出的 ArcFace 与相关基线方法的性能，例如 Softmax、Triplet、SphereFace 和 CosineFace。ArcFace 在干扰物细化之前和之后获得最佳性能。在从一百万个干扰物中移除重叠的人脸图像之后，识别性能显着提高。我们相信手动精炼的 MegaFace 数据集的结果更可靠，并且在数百万个干扰物下面部识别的性能比我们想象的更好。因此，可以理解的是，行业模型正在探索千万甚至十亿级别干扰者的人脸识别问题。

为严格遵循 MegaFace 上的评估说明，我们需要从训练数据中删除 FaceScrub 数据集中出现的所有身份。我们计算精炼的 MS1M 数据集和 FaceScrub 数据集中每个身份的特征中心。我们发现来自精炼 MS1M 数据集的578个身份与 FaceScrub 数据集中的身份具有近距离（余弦相似度高于 $0.45$）。我们从精炼的 MS1M 数据集中删除这578个身份，并将所提 ArcFace 与表Table 10中的其他基线方法进行比较。与表Table 9相比，ArcFace 性能略有下降但仍然优于 CosineFace。但是对于 Softmax 来说，在从训练数据中删除可疑的重叠身份后，识别率从 $78.89\%$ 下降到 $73.66\%$。在精炼的 MegaFace 测试集上，CosineFace 的验证结果略高于 ArcFace。这是因为我们从 devkit 的输出中读取了最接近 FAR=1e-6的验证结果。正如我们在图fig：megafacechallenges中所看到的，所提 ArcFace 在识别和验证指标下总是优于 CosineFace。

借助 Triplet Loss 进一步提升

由于 GPU 内存的限制，数百万个身份的数据很难使用基于 Softmax 的方法训练，例如 SphereFace、CosineFace 和 ArcFace。一个可行的解决方案是采用度量学习方法，最广泛使用的方法是 Triplet loss[22]。然而，Triplet loss 的收敛速度相对较慢。为此，我们探索以 Triplet loss 微调基于 Softmax 方法训练后的人脸识别模型。

对于三元组损失微调，我们使用 LResNet100E-IR 网络并将学习率设置为 $0.005$，动量为 $0$，权重衰减为 $5e-4$。如表Table 11所示，我们通过 AgeDB-30 数据集上的 Triplet 损失微调来提供验证准确性。我们发现

• 在具有较少身份编号的数据集（例如，具有8,631个身份的VGG2 ）上训练的 Softmax 模型，放到具有更多身份编号的数据集（例如，具有85k身份的MS1M）上用 Triplet 丢失进行微调，可以明显改善性能。这一改进证实了两步训练策略的有效性，与从头开始训练 Triplet 损失相比，该策略可以显着加速整个模型训练。
• 同一数据集上 Triplet 损失仍可微调进一步提升 Softmax 模型，这证明了局部细化可以改善全局模型。
• 优秀的边界改进 Softmax 方法，例如 SphereFace、CosineFace 和 ArcFace，可以通过 Triplet 损失微调来保持和进一步改进，这也验证了局部度量学习方法，例如 Triplet loss，是全局超球面度量学习方法的补充。

由于 Triplet 损失中使用的边界是欧几里德距离，我们最近将研究具有角度边界的 Triplet 损失。

Arcface 的 PyTorch 实现

原版 ArcFace 使用 MXNet 实现，这里介绍 PyTorch 上的第三方实现。

    # implementation of additive margin softmax loss in https://arxiv.org/abs/1801.05599    
    def __init__(self, embedding_size=512, classnum=51332,  s=64., m=0.5):
        super(Arcface, self).__init__()
        self.classnum = classnum
        self.kernel = Parameter(torch.Tensor(embedding_size,classnum))
        # initial kernel
        self.kernel.data.uniform_(-1, 1).renorm_(2,1,1e-5).mul_(1e5)
        self.m = m # the margin value, default is 0.5
        self.s = s # scalar value default is 64, see normface https://arxiv.org/abs/1704.06369
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        self.mm = self.sin_m * m  # issue 1
        self.threshold = math.cos(math.pi - m)

forward

l2_norm 会求导吗？

        # weights norm
        nB = len(embbedings)
        kernel_norm = l2_norm(self.kernel,axis=0)

torch.mm 执行矩阵mat1和mat2的矩阵乘法。
torch.clamp 将输入中的所有元素夹在[min，max]范围内并返回结果张量：
$$\begin{array}{r}{y}_i=\{\begin{array}{ll}\text{min}& \text{if }{x}_i<\text{min}\\ x_i& \text{if }\text{min}\le x_i\le \text{max}\\ \text{max}& \text{if }{x}_i>\text{max}\end{array}\end{array}$$
如果输入的类型为FloatTensor或DoubleTensor，则 args min和max必须是实数，否则它们应该是整数。

        # cos(theta+m)
        cos_theta = torch.mm(embbedings,kernel_norm)
#         output = torch.mm(embbedings,kernel_norm)
        cos_theta = cos_theta.clamp(-1,1) # for numerical stability
        cos_theta_2 = torch.pow(cos_theta, 2)
        sin_theta_2 = 1 - cos_theta_2
        sin_theta = torch.sqrt(sin_theta_2)
        cos_theta_m = (cos_theta * self.cos_m - sin_theta * self.sin_m)

$$f(n)=\{\begin{array}{ll}\cos (\theta +m)=\cos (\theta )\cos (m)-\sin (\theta )\sin (m)& \text{if }0\le \theta +m\le \pi \\ \cos (\theta )-\sin (m)\ast m& \text{else }\end{array}$$
因为 $0\le m\le \pi$ 且 $0\le \theta \le \pi$，所以例外情况仅需考虑 $\pi \le \theta +m$。又因为 $cos(x)$ 对于 $0\le x\le \pi$ 是单调递减函数，所以 $\pi -m\le \theta ⟺\cos (\theta )\le \cos (\pi -m)$

# this condition controls the theta+m should in range [0, pi]
        #      0<=theta+m<=pi
        #     -m<=theta<=pi-m
        cond_v = cos_theta - self.threshold
        cond_mask = cond_v <= 0
        keep_val = (cos_theta - self.mm) # when theta not in [0,pi], use cosface instead
        cos_theta_m[cond_mask] = keep_val[cond_mask]
        output = cos_theta * 1.0 # a little bit hacky way to prevent in_place operation on cos_theta
        idx_ = torch.arange(0, nB, dtype=torch.long)
        output[idx_, label] = cos_theta_m[idx_, label]
        output *= self.s # scale up in order to make softmax work, first introduced in normface
        return output

l2_norm

def l2_norm(input,axis=1):
    norm = torch.norm(input,2,axis,True)
    output = torch.div(input, norm)
    return output

参考资料：

• 【论文理解】ArcFace: Additive Angular Margin Loss for Deep Face Recognition（InsightFace）
• deepinsight/insightface
• 人脸识别（四）：2018 ArcFace: Additive Angular Margin Loss for Deep Face Recognition
• TreB1eN/InsightFace_Pytorch
• ronghuaiyang/arcface-pytorch