生信入门
题前语:
面对未知的前方每个人都可能些许迷茫,但是迷茫归迷茫,可千万不要忘记奋力奔跑。欢迎各位看到本篇内容的学弟学妹以及朋友们,我叫咩小饬,以下内容如有不足欢迎指出。
1. Linux基础
先说说为什么需要学习linux吧,因为在一个数据时代的今天,我们日常生活中接触到的数据越来越多,然而在很多行业首先你需要处理数据使用计算机运行数据对计算机的要求也是极为苛刻,然而windows与linux最大的差异就是性能问题,目前大火的大数据基本都是在linux系统下运行的,linux系统运行环境适用于数据处理。就这么简单!
- linux基本命令
cd 打开
./ 运行可执行文件
su 切换用户登录
mv 待移动文件位置 移动后的文件位置
cp 待复制文件位置 复制后的文件位置
rm 此操作为删除命令,后可跟多个参数运行。最基本的有:
rm 文件名
rm 携带参数 文件名或文件夹名称
解压缩命令:
tar -zxvf 压缩包名.tar.gz
debain系统下:
apt-get install 包名
centos系统下:
apt-get install 包名
题外话:
| LOCI | 死亡之 ping |
|---|---|
| nmap扫描 | nmap扫描 |
2. plink基本命令
-- plink
--ped 后跟.ped文件
--map 后跟.map文件
--merga 合并文件命令
--recode 转化文件
--out 输出文件
基本命令的使用
1. Plink进入D:
2. Cd D:\软件\plink
3. plink --ped 30.ped --map 30.map --recode vcf --out ped_to_vcf --sheep
4. 把要对比的文件选择出来转为TXT格式
注意:30.ped和30.map是要提前准备好的文件转化为ped_to_vcf
k分析:
plink --ped 30.ped --map 30.map --make-bed --out 1 --sheep
把bed、fam、bim文件放入虚拟机admixture文件夹打开终端
./admixture --cv 30.bed 2k|tee 2.out
Pca分析
plink --file loutput2.bed --pca 3 --sheep
3. 浅谈哈温定律
哈代-温伯格定律,也称遗传平衡定律或哈代-温伯格平衡定律,分别在1908年和1909年由英国数学家G·H·哈代(Godfrey Harold Hardy)和德国医生威廉·温伯格(Wilhelm Weinberg)独立证明。在群体遗传学中,哈代-温伯格定律主要用于描述群体中等位基因频率以及基因型频率之间的关系。主要内容为:
“ 一个群体在理想情况(不受特定的干扰因素影响,如非随机交配、天择、族群迁移、突变或群体大小有限),经过多个世代,基因频率与基因型频率会保持恒定并处于稳定的平衡状态。 ”
实际上,总会存在一个或多个干扰因素。因此,哈代-温伯格定律在自然界中是不太可能的。基因的平衡是一种理想状态,并用于测量遗传改变的基准。
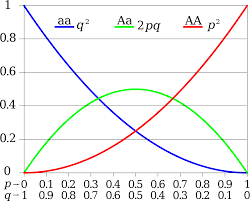
最简单的例子是位于单一位点的两个等位基因:显性等位基因记为A而隐性等位基因记为a,它们的频率分别记为p和q。频率(A) = p;频率(a) = q;p + q = 1。如果群体处于平衡状态,则我们可以得到
群体中纯合子AA的频率(AA) = p2
群体中纯合子aa的频率(aa) = q2
群体中杂合子Aa的频率(Aa) = 2pq
推导:
对于二倍体物种,考虑种群中两个独立的等位基因A和a,它们的频率分别是p和q。使用旁氏表推导出形成新基因型的不同方式,其中每一格的值为行与列概率的乘积。
4. vcftools基本使用
vcftools的基本安装
安装: vcftools sudo apt-get install vcftools(debain系统)
解压:
cd 文件位置。
tar zxvf 文件名
vcftools基本命令的使用
FST 分析
vcftools --vcf ped_to_vcf.vcf --weir-fst-pop CL.txt --weir-fst-pop DL.txt --fst-window-size 50000 --fst-window-step 25000 --out CLHDL.Fst
PI分析
vcftools --vcf ped_to_vcf.vcf --keep HT.txt --window-pi 50000 --out HTPI
Vcf文件转map和ped
vcftools --vcf 1664.vcf --keep locatedsheep.txt --recode --out located
5. 诉说R与绘图
R与绘图吧,说实话吧,人家刘哥喜欢,我并不太感冒。。。。那就。。算了,碍于刘哥面子我就贴个曼哈顿图的两种画法吧。
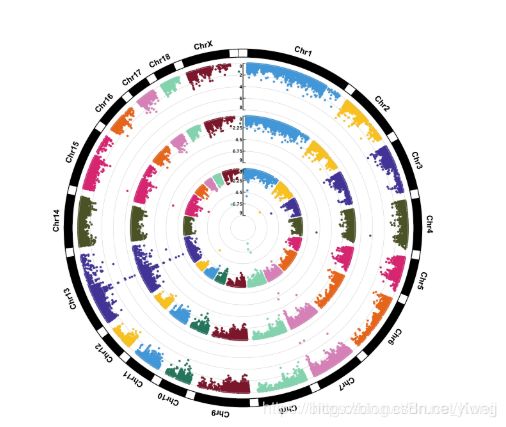
首先使用cmplot绘图包,绘制曼哈顿图:
s <- read.table("s.txt",header=T)
CMplot(s,type="p",plot.type="c",LOG10=FALSE,outward=TRUE,col=matrix(c("#4DAF4A",NA,NA,"dodgerblue4",
"deepskyblue",NA,"dodgerblue1", "olivedrab3", "darkgoldenrod1"), nrow=3, byrow=TRUE),
chr.labels=paste("Chr",c(1:26),sep=""),threshold=NULL,r=1.2,cir.chr.h=0.5,cir.legend.cex=0.5,
cir.band=1,file="jpg", memo="",dpi=300,chr.den.col="red",file.output=TRUE,verbose=TRUE,
width=5,height=10)
绘图完成。关键是函数里面参数的用法,一句话:多看文档,千万别偷懒,多看文档有益于提高你的变成水平。
首先载入数据:
#载入R包
#install.packages("qqman")
library(qqman)
library(tidyverse)
#查看原始数据
head(gwasResults)
SNP CHR BP P
1 rs1 1 1 0.9148060
2 rs2 1 2 0.9370754
3 rs3 1 3 0.2861395
4 rs4 1 4 0.8304476
5 rs5 1 5 0.6417455
6 rs6 1 6 0.5190959
我们知道Manhattan图实际就是点图,横坐标是chr,纵坐标是-log(Pvalue) ,原始P值越小,-log转化后的值越大,在图中就越高。
原始数据中重要的“元素”都有了 ,我们自己的数据也是只需要这四列就可以了。注意绘制前需要转化一下:
处理原始数据,计算snp位点的累计位置:
1.计算染色体长度
chr_len <- gwasResults %>%
group_by(CHR) %>%
summarise(chr_len=max(BP))
2.计算每条染色体的初始位置
chr_pos <- chr_len %>%
mutate(total = cumsum(chr_len) - chr_len) %>%
select(-chr_len)
3.计算累计SNP的位置
Snp_pos <- chr_pos %>%
left_join(gwasResults, ., by="CHR") %>%
arrange(CHR, BP) %>%
mutate( BPcum = BP + total)
4.查看转化后的数据
head(Snp_pos,2)
SNP CHR BP P total BPcum
1 rs1 1 1 0.9148060 0 1
2 rs2 1 2 0.9370754 0 2
6. 说说python与绘图
- 基本语法
想学python的同学我可以认真推荐一门网课,B站小甲鱼的基础入门python这个网课讲的知识点十分细化适用于没有编程基础的初学者。关键是他的讲课也很少的枯燥,相信很多人可以坚持学完,相信很多人学完了编程基础那么真正的重头戏就要来了。python的数据分析与可视化。说到这个首先入门基础就是numpy+pandas+matplotlib三剑客了,在数据分析领域它们三占据着重要地位,至于怎么学?首先就是需要拥有python基础。正所谓“基础不牢,地动山摇。”所以,基础还是很重要滴,等你有一天学完这些了,发现做图的要求越来越高,matplotlib做出的图形很难满足你了,那么我推荐pyecharts吧。这个是由百度开发的一个兼容python的框架,这个框架真的是非常好用,而且最为关键的一点就是,由于百度开发的嘛!它有中文文档!对于英语渣渣的我来说简直不要太幸福的吗。(补充一句:pyecharts可以做出来动态的数据可视化图,但是安装的时候需要注意0.5版本与1.0有重大的更新,我一般使用1.0啦。0.5版本不再做维护了哟。)
贴几张pyecharts做的图表让各位感受一下吧:
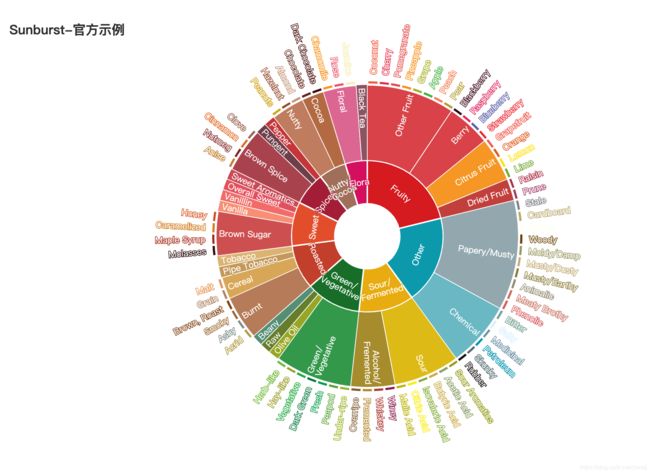
pyecharts官方中文文档