李宏毅机器学习——循环神经网络(一)
引言
今天来介绍一下循环神经网络(Recurrent Neural Network,RNN),和现在比较常用的长短期记忆网络(LSTM)。并且通过多个例子来阐述这些概念,个人觉得还是比较容易理解的。
循环神经网络
我们以一个例子来引入RNN,这个例子就是填槽(Slot Filling)。
假设你要做一个智能订票系统。

假设有个人对你的订票系统说:“I would like to arrive Taipei(台北) on November 2nd.”,
作为一个订票系统,里面肯定会有像目的地(desination)和到达时间(time of arrival)这种关键信息。这里就用slot表示,你的系统要通过上面说的话就能识别出来目的地是Taipei,到达时间是:November 2nd。其他的词汇就不属于任何Slot。
这个问题可不可以用一个前馈神经网络来解,输入是一个词汇,比如把Taipei变成一个向量,丢到NN中去,但是在这之前你必须先把这个词汇用一个向量来表示。
![]()
把词汇用向量表示的方法有很多,最简单的方法是1-of-N编码。假设现在你的训练数据里面只有5个词汇,那么你就可以用一个5维向量表示,每个维度对应一个向量。出现某个词,就将对应维度的值设成1,其他都为0。

如果测试数据中出现了你训练数据中没有的词汇,那怎么办呢,有一种办法是增加一个维度,专门用来表示没有见过的词汇,这里用"other"表示。

除了这种方法外,还有一个Word Hasing的方法。
用某个词汇的字母来表示它的向量,比如有个词汇叫“apple”,“apple”里面有出现“app”、“ppl”和“ple”。在这个向量,对应中上面三个维度的值就是1,其他的都是0。
这样我们就能把一个词汇表示成一个向量,然后丢到NN中去,在填槽任务中,你希望这个前馈NN的输出是一个概率分布。这个概率分布代表我们输入的每个词汇属于每个SLOT的概率。

举例来说,就是Taipei属于这两个SLOT的概率。
如果仅是如此是不够的。

假设有人说“arrive Taipei on November 2nd”,这里面“Taipei”是目的地,“November 2nd”是时间,剩下的不属于这两个SLOT。
假设你解决了这个问题,但是另一个人说:“leave Taipei on November 2nd”。

那此时的Taipei应该是出发地,但是对于NN来说,输入是一样的东西,输出就是一样的东西。
你输入Taipei这个词汇,它输出要么都是目的地的概率最高,要么都是出发地(这里引入了一个新的SLOT)的概率最高。
你无法让同样的输入有时出发地的概率最高,有时目的地的概率最高。

如果NN是有记忆的就好了,如果它在看过红色的Taipei之间就已经看过arrive这个词汇;它记得它在看过绿色的Taipei之间,看过leave这个词汇。它就可以根据对话的上下文产生不同的输出!
这样就能解决输入是同样的词汇,输出是不同的问题。
这种有记忆的神经网络就是RNN(具体的说应该是简单的RNN(SimpleRNN))。

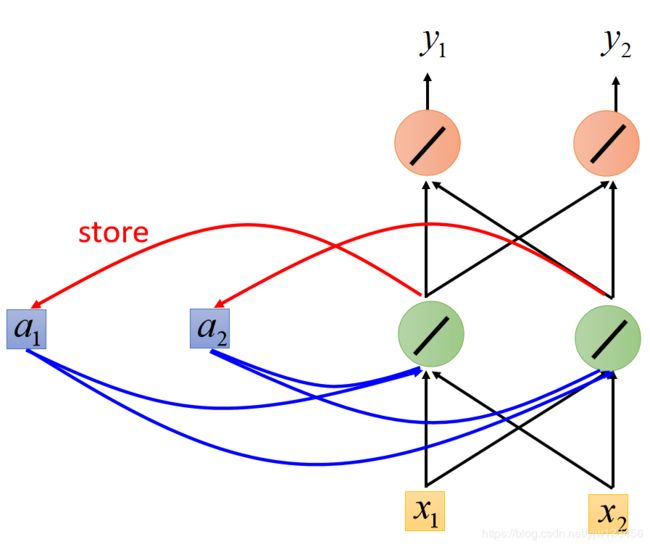
在RNN里面,每次我们的隐藏层产生输出的时候,这个输出都会被存到内存里面去。
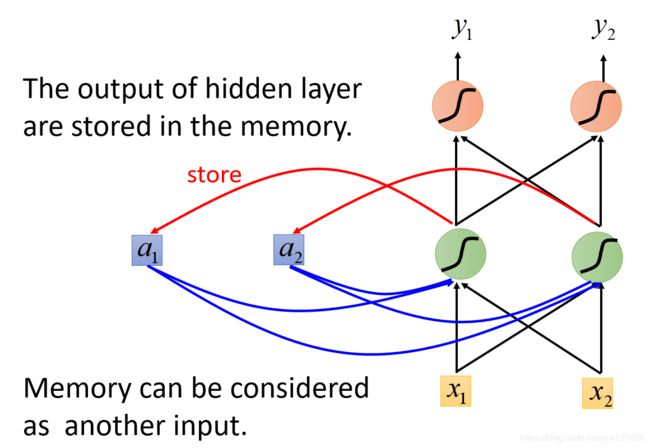
那么在下次有输入的时候,此时这个NN就不仅会考虑输入的 x 1 , x 2 x_1,x_2 x1,x2,还会考虑存在内存中的值。它们都会影响这个隐藏层的输出。
假设我们现在图上的NN所有的权重都是 1 1 1,并且所有的神经元都没有任何的偏置( b b b),同时假设所有的激活函数都是线性的。
假设我们的输入是这样的序列:
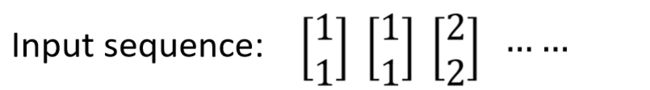
接下来在使用我们的RNN之前需要给 a 1 , a 2 a_1,a_2 a1,a2初始值。
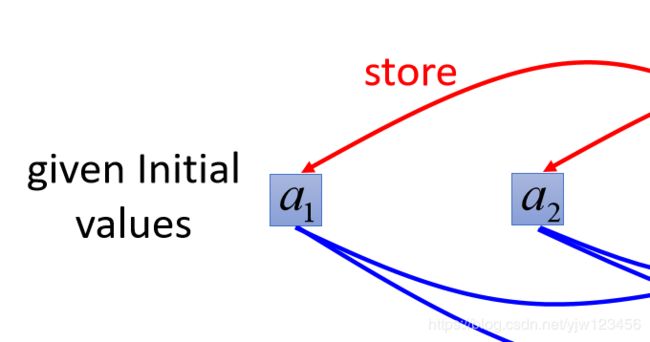
这里假设里面的初始值是 0 0 0。

以上面用红框框出来的神经元来说,它不仅接到我们输入的1和1,它还接到内存中的0和0。
因为我们说所有的权重 w w w都是1,因此它的输出为: 0 ( a 1 ) × 1 ( w ) + 0 ( a 2 ) × 1 + 1 ( x 1 ) × 1 + 1 ( x 2 ) × 1 = 2 0(a_1)\times 1(w) + 0(a_2)\times 1 + 1(x_1)\times 1 + 1(x_2)\times1 = 2 0(a1)×1(w)+0(a2)×1+1(x1)×1+1(x2)×1=2 括号里面是解释对应的值是怎么来的。

同样,隐藏层右边的神经元输出也是2。
接下来,根据同样的计算方法,红色两个神经元的输出都是4。
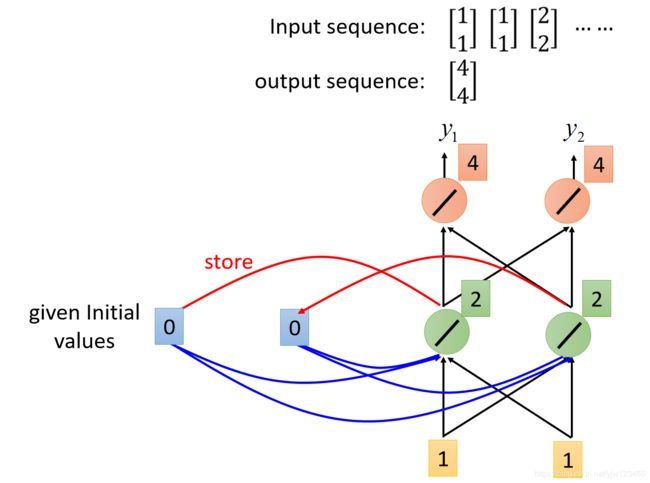
因此,输入是1和1的时候,输出就是4和4。
接下来RNN会把绿色神经元的输出存到内存中去,覆盖之前的0和0。

接下来再输入第二个1和1,这时绿色的神经元的输出就会是: 2 × 1 + 2 × 1 + 1 × 1 + 1 × 1 = 6 2 \times 1 + 2\times 1 + 1\times1 + 1\times1 = 6 2×1+2×1+1×1+1×1=6。
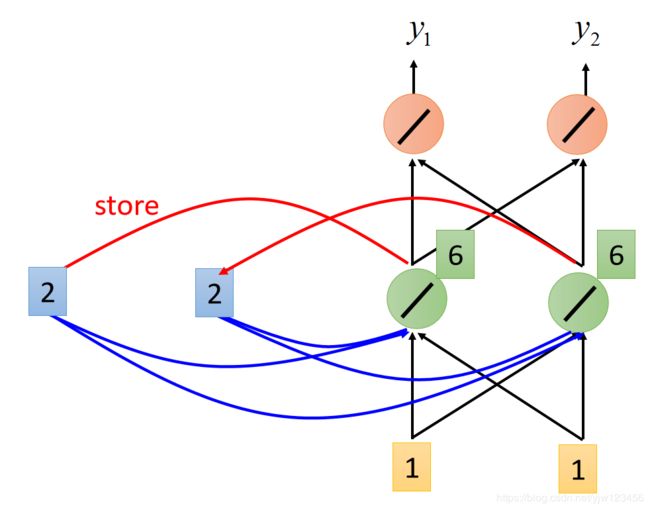
最后红色神经元的输出就是 6 × 1 + 6 × 1 = 12 6 \times 1 + 6\times 1 = 12 6×1+6×1=12。
所以当输入第二个1和1的时候,输出就是12和12。

所以从这里可以看出,对于RNN来说,就算给它一样的东西,也能得到不一样的结果。因为存在内存中的值是不一样的。
别忘了,接下来还会把绿色神经元的输出6和6覆盖掉之前的2和2。

接下来输入就是2和2,
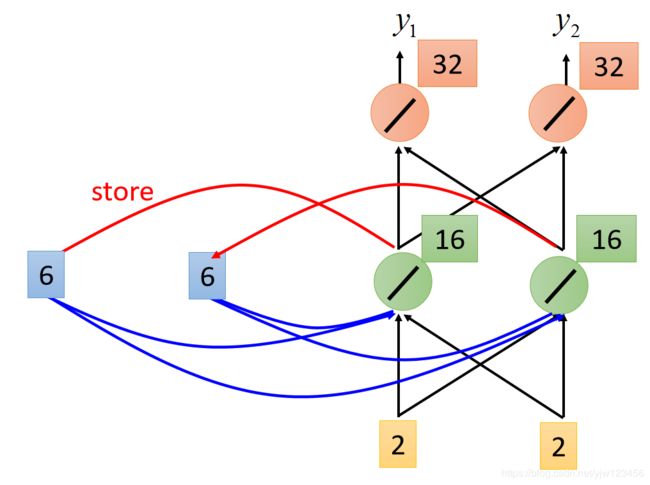
根据同样的方法,就可以计算出绿色神经元的输出是16,红色神经元的输出是32。
当输入2和2时,输出就是32和32。

在做RNN的时候,有个很重要的是,输入序列的顺序会影响输出。

所以我们要用RNN来处理填槽问题的话,它就可以就像下面这样。
有个人说:“arrive Taipei on November 2nd”。
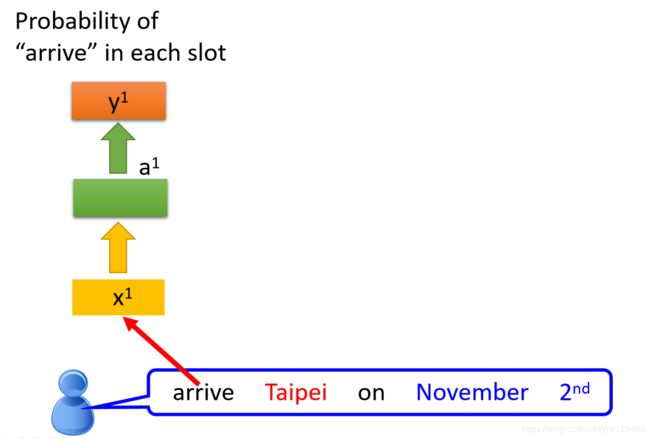
arrive就变成了一个向量,丢到NN中去,它的隐藏层输出是 a 1 a_1 a1(也是个向量),然后根据 a 1 a_1 a1我们产生 y 1 y^1 y1,就是arrive属于每个SLOT的概率。
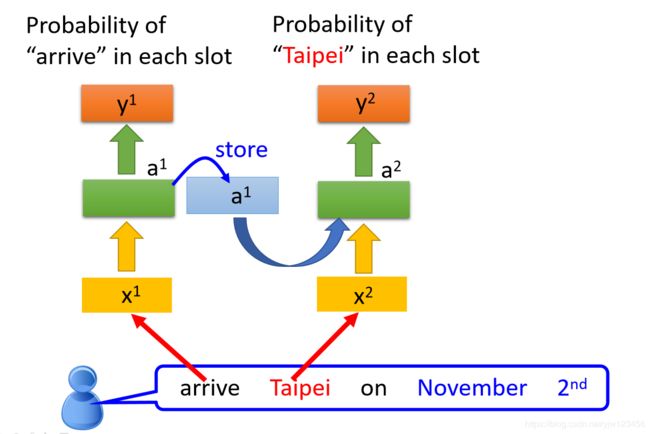
接下来 a 1 a_1 a1会被存在内存中去,并且Taipei会变成输入,这个隐藏层会同时考虑Taipei这个输入和存在内存中的 a 1 a_1 a1,得到 a 2 a_2 a2,在根据 a 2 a_2 a2产生 y 2 y^2 y2, y 2 y^2 y2是Taipei属于每个SLOT的概率。
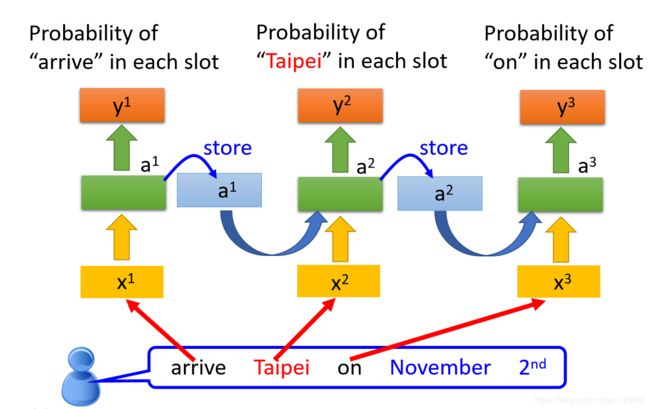
以此类推,我们就把 a 2 a_2 a2存到内存中去,再把on丢进去,然后产生 a 3 a_3 a3,进而产生 y 3 y^3 y3。
上面其实只是同一个神经网络,只是内存中保存的值不同,这里被使用了3次。
所以当神经网络有了记忆以后,刚才我们讲的输入同一个词汇,我们希望输出不同的问题就有可能被解决。
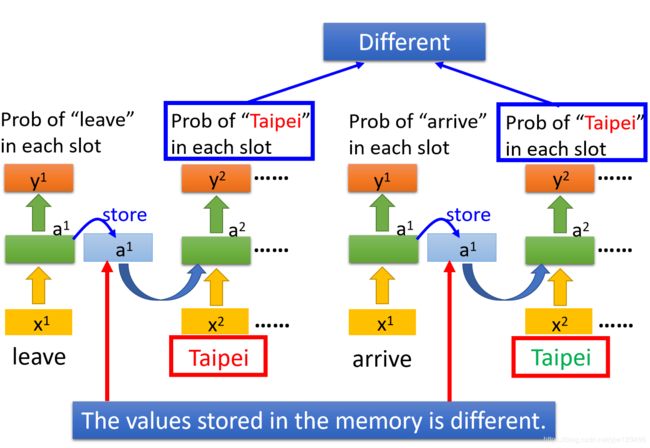
比如说,同样是输入了Taipei这个词汇,红色的前面接的是leave,绿色的Taipei前面接的是arrive。因为leave和arrive的向量不一样,所以存在内存中的值就不一样,这样最终得到的输出也不一样。
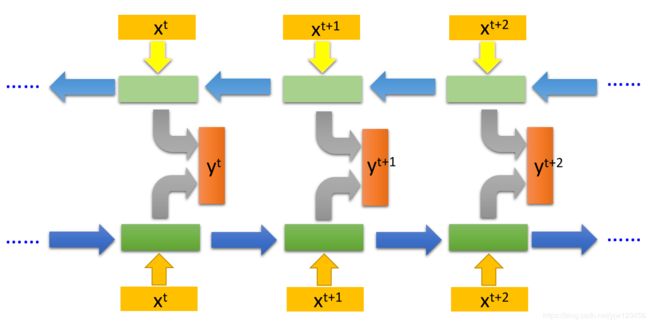
这个RNN的基本概念,虽然我们这里只有一个隐藏层,其实是可以很深的。

比如把 x t x^t xt丢进去后,它可以通过很多个隐藏层,最后得到输出 y t y^t yt。
每个隐藏层的输出都会存在内存中,下个时间点的时候,每个隐藏层都会读出前个时间点存的值,最后得到最终的输出,整个过程如下:

Elman Network & Jordan Network
RNN有不同的变形,我们刚才讨论的是Elman Network,就是把隐藏层的输出值存起来,下个时间点再读出来。如下图:
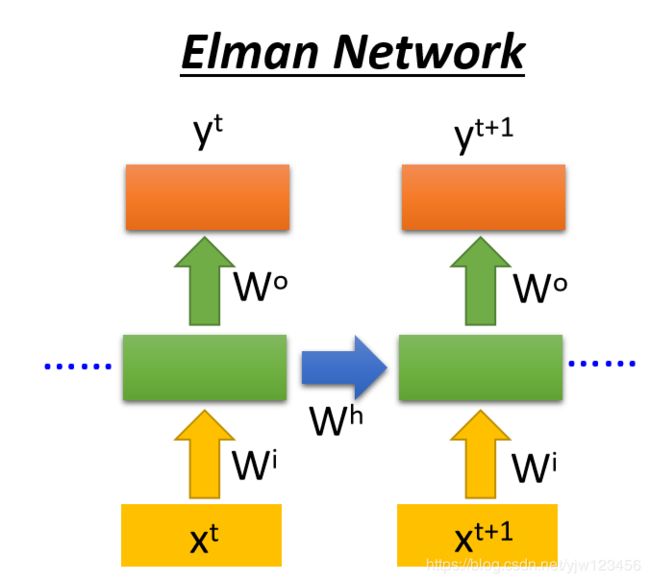
还有一种是Jordan Network,它存在的整个网络(这里用网络)的输出值,它会把这个输出值在下个时间点读进来。

据说Jordan Network能有比较好的结果,因为Elman Network的隐藏层的输出是没有目标的,你很难控制它学到怎样的东西;而输出值 y y y是有目标的,我们可以很清楚知道我们放到内存中的是什么。
双向循环神经网络(Bidirectional RNN)
RNN还可以是双向的,我们刚才看到的RNN是输入一个句子,从句首读到句尾。

比如说,先读 x t x^t xt,再读 x t + 1 x^{t+1} xt+1,再读 x t + 2 x^{t+2} xt+2

但是,它的读取方向其实是可以反过来的。可以先读 x t + 2 x^{t+2} xt+2,再读 x t + 1 , 最 后 读 x^{t+1},最后读 xt+1,最后读x^t$。
我们可以同时训练正向的RNN和逆向的RNN,然后把这两个RNN的隐藏层拿出来,都接给一个输出层,产生 y y y。
用双向循环神经网络的好处是,你的网络在产生输出的时候,它看的范围是比较广的。如果你只有正向的RNN,在产生 y t , y t + 1 y^t,y^{t+1} yt,yt+1的时候,你的网络只看过 x 1 x^1 x1一直到 x t + 1 x^{t+1} xt+1的输入。
如果我们今天是双向循环神经网络的时候,在产生 y t + 1 y^{t+1} yt+1的时候,你的网络不仅看了 x 1 x^1 x1到 x t + 1 x^{t+1} xt+1的输入,它也看了从句尾一直到 x t + 1 x^{t+1} xt+1的输入。
你的网络等于是看了整个输入的序列以后,才决定每个词汇的SLOT应该是什么。当然会比只看了句子的一般得到更好的结果。
长短期记忆网络
刚才讨论的RNN的内存版本只是最简单的,接下来我们讨论下 长短期记忆网络(Long Short-term Memory,LSTM)。
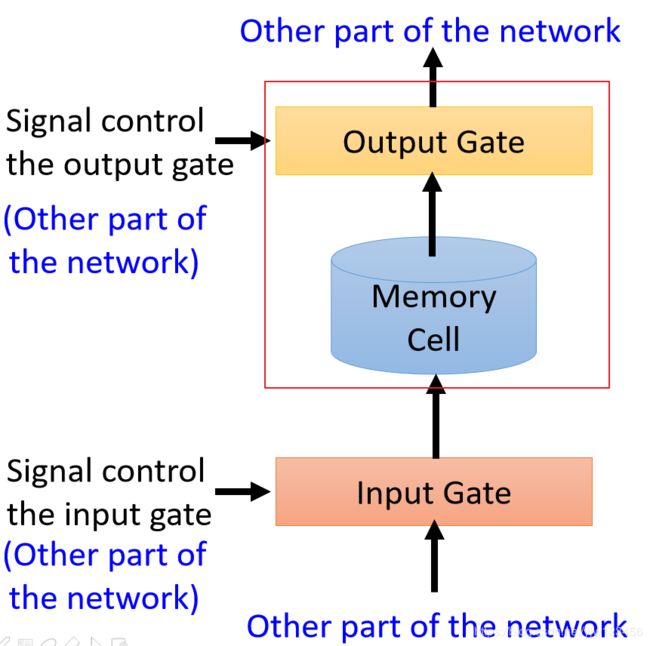
我们现在有个Memory Cell,它就像我们刚才说的RNN中隐藏层的内存。
LSTM它的Memory Cell有三个门结构,当神经网络的输出想要写到内存Memory Cell中去时,它必须先通过一个输入门(Inpute Gate),这个输入门打开的时候才能把值写到Memory Cell中去,如果关闭的时候是无法写进去的。
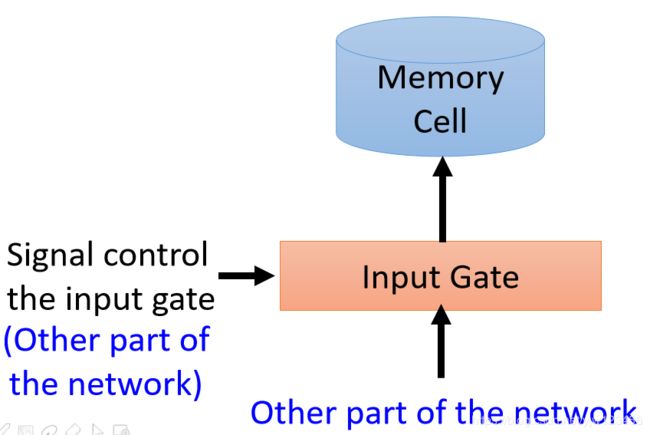
这个输入门是打开还是关闭是神经网络自己学的。
在输出的地方也有一个输出门(Output Gate),这个输出门会决定外界(其他的神经元)能否从这个Memory Cell中读出值。只有打开的时候才能读出值。和输入门一样,输出门什么时候打开,什么时候关闭,也是神经网络自己学习的。
第三个门是遗忘门(Forget Gate),它来决定Memory Cell是否要忘掉之前保存的值。

同样,什么时候要忘掉,什么时候要保存也是网络自己学到的。

整个LSTM你可以看成是一个特征的神经元,它有4个输入和1个输出。
这个四个输入是:想要存到Memory Cell中的值、操控输入门的讯号(决定能否存进去)、操控输出门的讯号(决定别人能否看到)以及操控遗忘门的讯号(决定是否要清除当前保存的值)。
这里应该是更“专业”的图例:
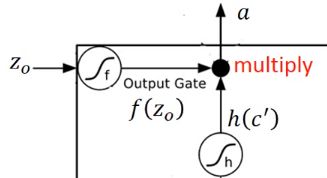
我们假设现在要存到Cell中的输入是 z z z,操作输入门的数值(标量)是 z i z_i zi,操控输出门的数值是 z o z_o zo,操控遗忘门的数值是 z f z_f zf,综合这些东西后得到的输出是 a a a。

假设在输入 z z z之前,Cell里面已经存了值 c c c。
然后我们输入 z z z,将 z z z通过激活函数(都是与它们自己相邻的那个)得到的值记为 g ( z ) g(z) g(z), z i z_i zi通过另外一个激活函数得到 f ( z i ) f(z_i) f(zi),这三个门机构的激活函数通常会选择Sigmoid函数。
因为Sigmoid函数的值是在0到1之间的,这个值可以代表这个门被打开的程度,如果经过Sigmoid函数后的输出是1,代表门是打开的;反之,0代表门是关闭的。

接下来就把 g ( z ) g(z) g(z)乘上输入门的值: f ( z i ) f(z_i) f(zi),得到 g ( z ) f ( z i ) g(z)f(z_i) g(z)f(zi)。
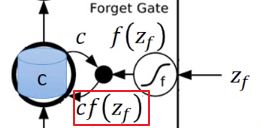
z f z_f zf也通过激活函数得到 f ( z f ) f(z_f) f(zf),接下来把存在Cell中的值 c c c乘上 f ( z f ) f(z_f) f(zf)得到: c f ( z f ) cf(z_f) cf(zf),然后把 c f ( z f ) cf(z_f) cf(zf)加上 g ( z ) f ( z i ) g(z)f(z_i) g(z)f(zi)得到 c ′ c^\prime c′,它就是新的存在Cell中的值。

根据目前为止的运算你可以发现, f ( z i ) f(z_i) f(zi)就是控制 g ( z ) g(z) g(z)能否输入的一个关卡,假设 f ( z i ) = 0 f(z_i)=0 f(zi)=0,那么不管你输入什么, g ( z ) f ( z i ) = 0 g(z)f(z_i)=0 g(z)f(zi)=0,就像是没有输入一样。
如果 f ( z i ) = 1 f(z_i)=1 f(zi)=1,那就把 g ( z ) g(z) g(z)当做输入。
而 f ( z f ) f(z_f) f(zf)决定是否要把存在Cell中的值清掉,假设 f ( z f ) = 1 f(z_f)=1 f(zf)=1,也就是遗忘门被开启的时候,这个时候 1 × c 1 \times c 1×c,会得到 c c c,然后把 c + g ( z ) f ( z i ) c + g(z)f(z_i) c+g(z)f(zi)写回去,相当于就会保存(用到)之前的值;如果 f ( z f ) = 0 f(z_f)=0 f(zf)=0,也就是遗忘门关闭, 0 × c 0 \times c 0×c得到 0 0 0,把 0 + g ( z ) f ( z i ) 0 + g(z)f(z_i) 0+g(z)f(zi)写到Cell中去,就相当于忘掉了(没用到)原来的 c c c。

然后把这两个值加起来写到Cell中去。遗忘门的开关和我们的直觉是相反的,打开的时候是记得,而关闭的时候是遗忘。或许应该叫它记忆门。

然后把这个 c ′ c^\prime c′通过 h h h这个激活函数,得到 h ( c ′ ) h(c^\prime) h(c′),接下来有一个输出门,这个输出门受 z o z_o zo所操控, z o z_o zo通过 f f f得到 f ( z o ) f(z_o) f(zo),然后会把 f ( z o ) f(z_o) f(zo)乘上 h ( c ′ ) h(c^\prime) h(c′)得到 a = h ( c ′ ) f ( z o ) a = h(c^\prime)f(z_o) a=h(c′)f(zo)。
如果 f ( z o ) = 1 f(z_o)=1 f(zo)=1,表示 h ( c ′ ) h(c^\prime) h(c′)可以通过这个输出门,反之如果是0,就表示这个输出就会变成0,也就是存在内存中的值就无法通过输出门被读取出来。
一个良心的例子
如果你没理解上面所说的,接下来用一个例子,结合上面说的,再描述一遍,希望你能明白。

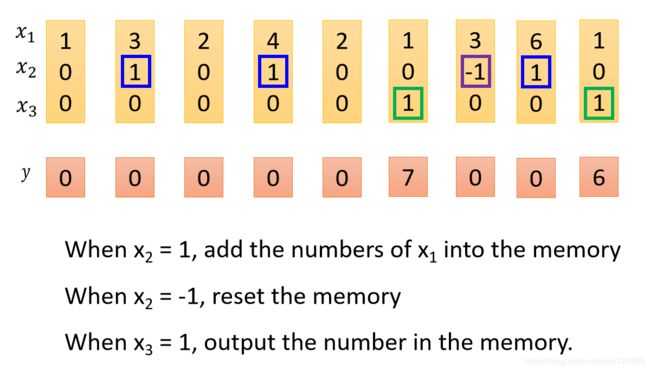
假设我们的网络中只有一个LSTM的Memory Cell,我们的输入是3维的向量,输出都是1维的向量。
- 当输入向量第2个维度 x 2 x_2 x2的值是1的话( x 2 = 1 x_2=1 x2=1), x 1 x_1 x1的值就会被写到内存中去
- 当 x 2 = − 1 x_2=-1 x2=−1时,内存中存的值就会被遗忘
- 当 x 3 = 1 x_3=1 x3=1时,才会打开输出门,看到输出。
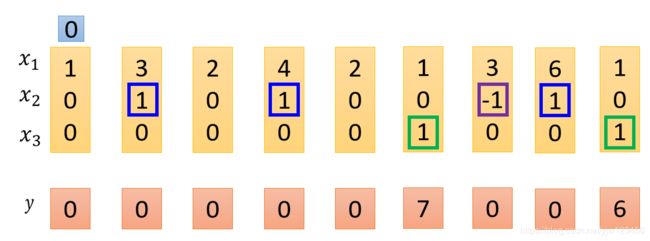
假设我们原来存到内存中的值是 0 0 0,当这边 x 2 = 1 x_2=1 x2=1时, 3 3 3会被存到内存中去,所以得到的值就变成 3 3 3。

接下来又出现了 x 2 = 1 x_2=1 x2=1的情况,所以 4 4 4就会被存到内存中去,加上之前的 3 3 3得到 7 7 7。

接下来遇到 x 3 = 1 x_3=1 x3=1,所以现在内存中的值 7 7 7就会被输出。
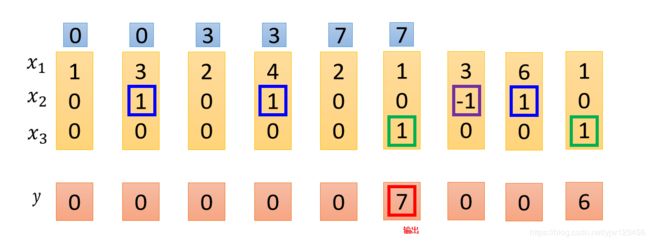
下面碰到了 x 2 = − 1 x_2=-1 x2=−1就会忘掉内存中的值,下一个时间点内存中的值就变成了 0 0 0
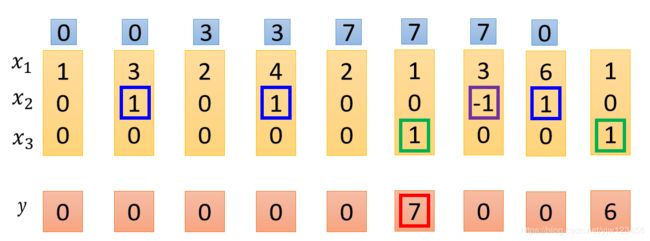
然后看到 x 2 = 1 x_2=1 x2=1就会把此时 x 1 x_1 x1的值 6 6 6存进去。

并且看到 x 3 = 1 x_3=1 x3=1,会把 6 6 6输出。
接下来就来实际做一下运算。

这是一个LSTM的Memory Cell,我们知道它有4个输入标量,这4个标量就是我们输入的3维向量乘上一个权重后加上偏差所得到的的结果。
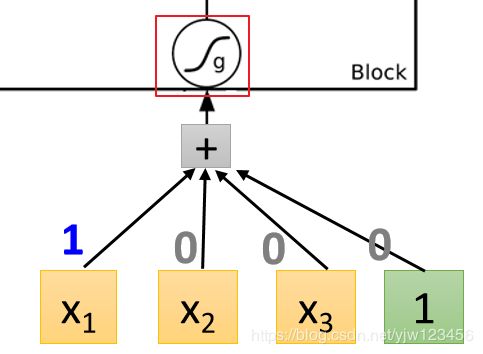
比如 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3与权重进行线性转换并加上偏差后就会得到一个标量,就得到这里的输入。
这里的权重与偏差都是通过训练数据学到的,这里假设我们已经知道这些值是多少。
这里假设我们的输入是:
![]()
我们来实际运算一下,不过在这之前,先分析一下我们可能会得到的结果。
先看整个Cell的输入这里
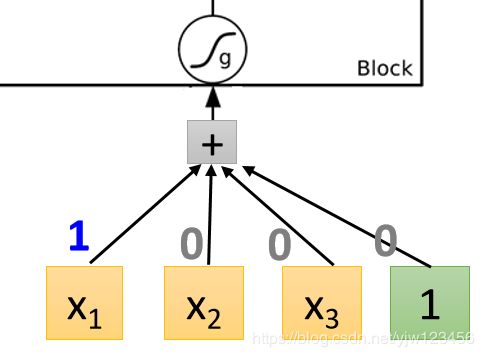
x 1 x_1 x1乘 1 1 1,其他都是乘 0 0 0,因此这里会直接把 x 1 x_1 x1当成输入。
再看输入门的地方
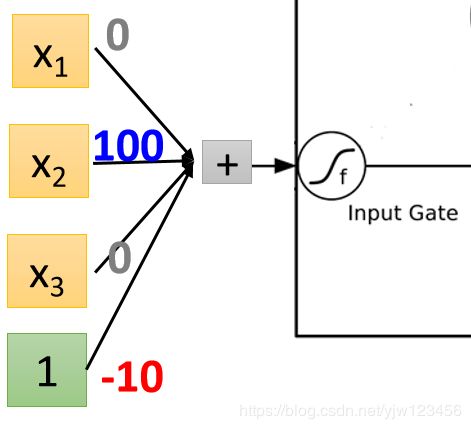
它是 x 2 × 100 x_2 \times 100 x2×100而偏差是 − 10 -10 −10,就是说假设 x 2 x_2 x2没有值时,经过运算就会得到偏差 − 10 -10 −10,经过Sigmid激活函数后,它的值会接近 0 0 0,这相当于输入门是关闭的,只有在 x 2 x_2 x2有值的时候,才有可能得到的结果比 − 10 -10 −10要大,经过Sigmoid函数得到一个正值,代表输入门被打开。
在看遗忘门这里
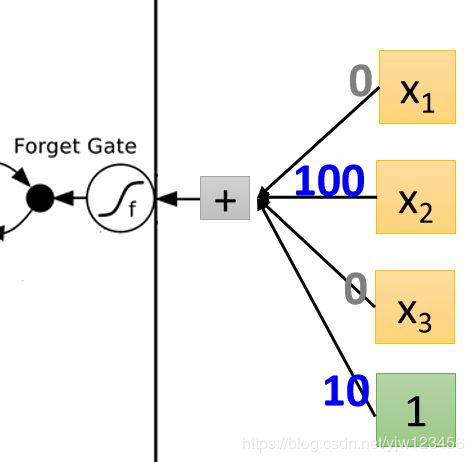
这里哪怕 x 2 x_2 x2没值也会被打开,因为偏差有个正值 10 10 10,只有在 x 2 x_2 x2有个很大的负值能压过偏差的时候,才会关闭。
最后看下输出门

输出门通常是关闭的,因为偏差是个较大的负值,如果 x 3 x_3 x3的正值可以压过偏差的话,就可以把输出门打开。
好了,接下来就可以实际手撸一把了。

这里为了简化计算,假设 g , h g,h g,h都是线性的,并且内存中的初始值是 0 0 0。
现在我们输入第一个向量 { 3 , 1 , 0 } \{3,1,0\} {3,1,0}。
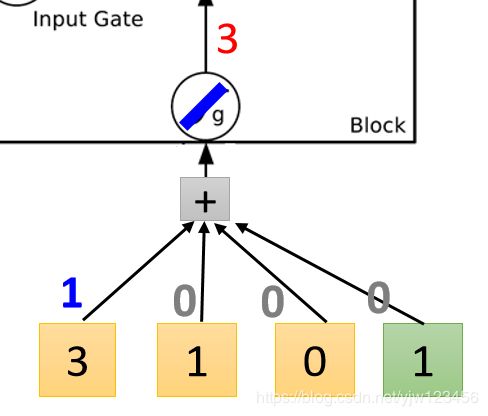
先看输入这里, 3 × 1 = 3 3 \times 1=3 3×1=3,因为其他的权重为 0 0 0,这里得到的输入就是 3 3 3。
然后再输入门这里

1 × 100 − 10 = 90 1 \times 100 - 10=90 1×100−10=90代入Sigmoid激活函数约等于 1 1 1,这里输入门就打开。
然后就可以通过输入门, 1 × 3 = 3 1\times 3=3 1×3=3
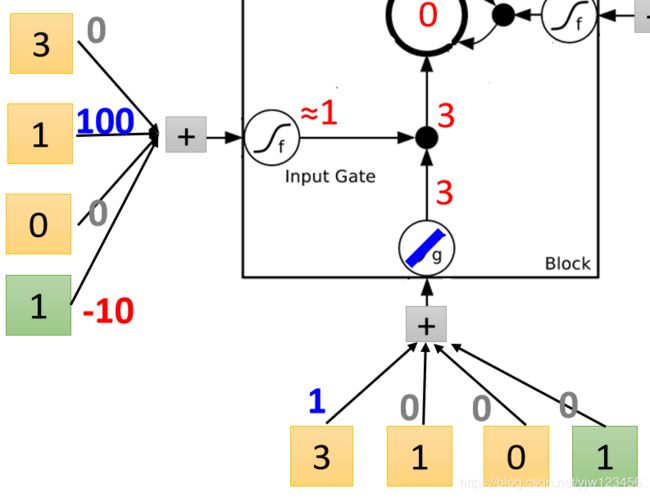
此时再来看下遗忘门

1 × 100 + × 10 = 110 1 \times 100 + \times 10 = 110 1×100+×10=110代入Sigmoid函数得到 1 1 1,遗忘门被打开,意思不会遗忘。
然后把Memory Cell中的 0 × 1 + 3 = 3 0 \times 1 + 3 = 3 0×1+3=3
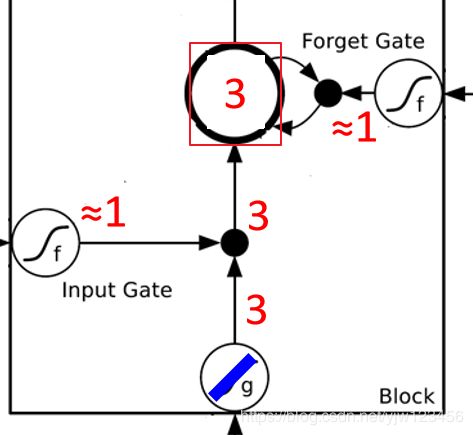
所以 3 3 3就会被存入Memory Cell。接下来看下输出门。
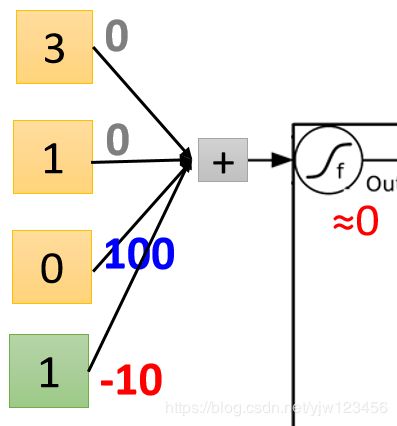
0 × 100 − 10 = − 10 0 \times 100 - 10 = -10 0×100−10=−10代入激活函数约等于 0 0 0,说明输出门关闭,也就是值无法输出,为什么
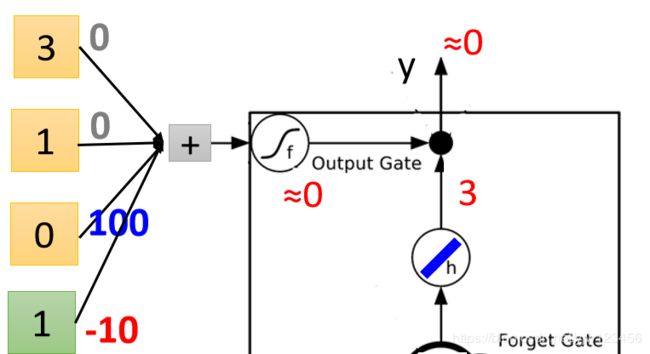
因为我们把输出门得到的 0 0 0乘以遗忘门传过来的 3 3 3 得 0 0 0,就是最终的输出值,被 0 0 0给消掉了。
接下来输入 { 4 , 1 , 0 } \{4,1,0\} {4,1,0}。

首先输入的值是 4 4 4,然后输入门是打开的,然后遗忘门也是打开的,所以内存中的值就变成了 3 × 1 + 4 = 7 3 \times 1 + 4 = 7 3×1+4=7,因此更新内存中的值为 7 7 7。
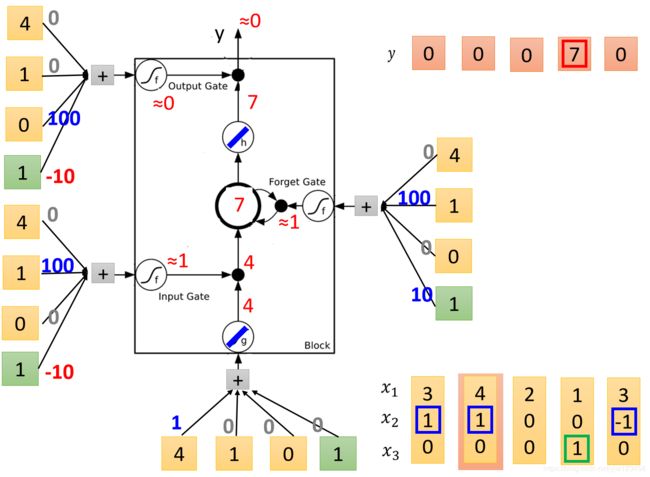
但是在这个输入( { 4 , 1 , 0 } \{4,1,0\} {4,1,0})下,输出门还是关闭的,导致 7 7 7也无法输出,输出的是 0 0 0。
接下来输入 { 2 , 0 , 0 } \{2,0,0\} {2,0,0}。
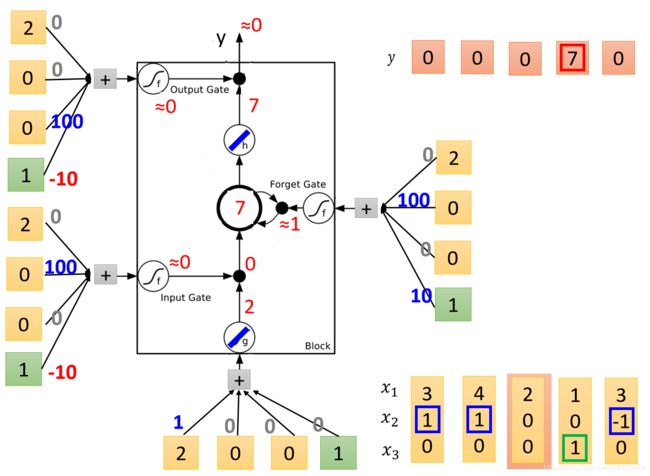
输入变成了 2 2 2,输入门经过计算是关闭的, 2 2 2乘以输入门的 0 0 0得到 0 0 0。
遗忘门是打开的 7 × 1 + 0 = 7 7 \times 1 + 0 =7 7×1+0=7,相当于内存中的值不变。此时输出门还是关闭的,最终输出是 0 0 0。
接下来输入 { 1 , 0 , 1 } \{1,0,1\} {1,0,1}。
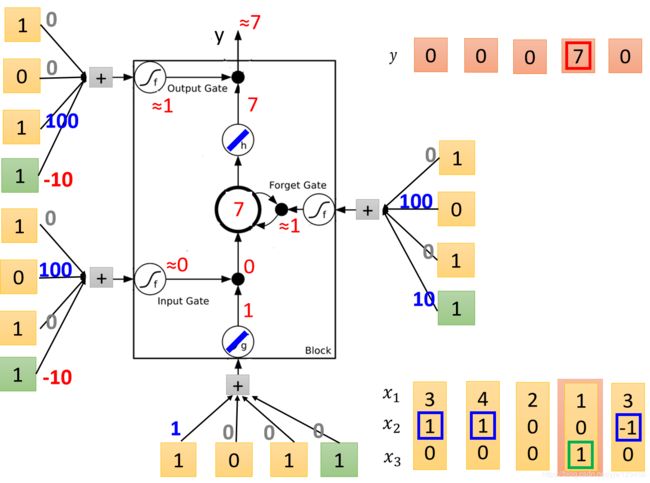
输入变成了 1 1 1,输入门是关闭的,遗忘门是打开的,内存中的值不变。但是此时输出门是打开的,我们把输出门的 1 1 1乘上传过来的 7 7 7,得到最终的输出是 7 7 7。
最后输入 { 3 , − 1 , 0 } \{3,-1,0\} {3,−1,0}。
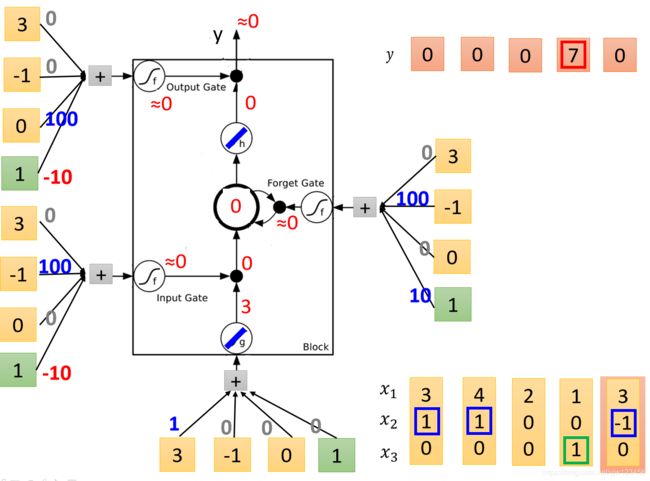
输入变成了 3 3 3,输入门是关闭的,遗忘门也是关闭的,所以内存中的值就变成了 0 × 3 + 7 × 0 = 0 0 \times 3 + 7 \times 0 = 0 0×3+7×0=0,输出门也是关闭的,不过此时哪怕打开了输出也是 0 0 0。
演算完毕。

看到这个东西我们可能觉得和原来的神经网络不像,在我们原来的神经网络里面会有很多神经元,我们会把输入乘上不同的权重,得到的值当成不同神经元的输入,
每个神经元都是一个函数,输入一个标量,输出另一个标量。
如果是LSTM的话,只要把LSTM的Memory Cell想成是一个神经元就好了。
现在的输入会乘上不同的权重,当做LSTM的不同的输入。这里假设这个隐藏层只有两个神经元。

x 1 , x 2 x_1,x_2 x1,x2乘上某组权重会去操控第一个LSTM的输出,再乘上另外一组权重操控输出门,乘上另外一组权重会去操控第一个LSTM的输入门,再乘上一组权重去操纵遗忘门。
第二个LSTM也是一样, x 1 , x 2 x_1,x_2 x1,x2乘上不同的权重去操控第二个LSTM的输入、输出门、输入门和遗忘门。
因此对应LSTM会有4倍的参数数量。因为每组权重不同,同一个输入 x 1 , x 2 x_1,x_2 x1,x2得到的乘以权重得到的值也是不一样的。
也即使LSTM需要4个输入才会产生一个输出,而原来的神经元只要一个输入就能产生一个输出。
但是看起来还是不太像RNN,这里画另外一个图来表示它。
假设我们有一整排的神经元(LSTM),每个LSTM的Cell中都存了一个标量,把这些标量连接起来就得到一个向量 c t − 1 c^{t-1} ct−1(表示时间点 t t t的前一个时间点)。每个LSTM存的值在这个向量的某个维中。
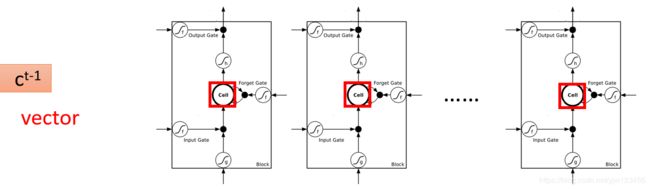
现在在时间点 t t t,有个输入向量 x t x^t xt,它首先会乘上一个矩阵进行线性转换变成另外一个向量 z z z。 z z z这个向量的每个维度代表了操控每个LSTM的输入。
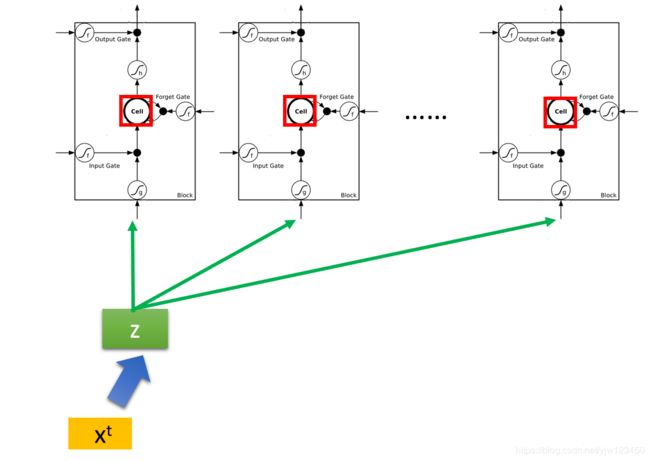
它的第一维就丢给第一个Cell,第二维就丢给第二个Cell…
这个 x t x^t xt会乘上另外一个矩阵得到 z i z^i zi。 z i z^i zi的维度也和LSTM的数量一样,不过它的每个维度操控的是LSTM的输入门。

看到这里你可能会想到,还有有两个新的向量来操控输出门与遗忘门。对了。
同样滴,得到 z f z^f zf来操控遗忘门, z o z^o zo操控输出门。
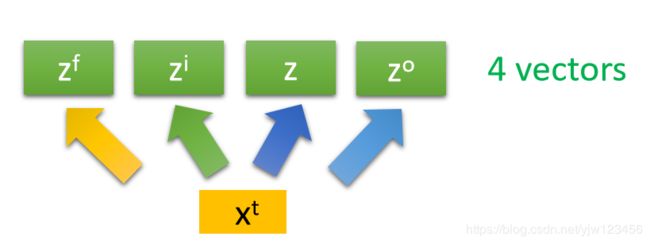
所以我们把 x t x^t xt乘上4个不同的矩阵,得到四个不同的向量。它们的维度都会LSTM的数量一样,这4个向量一起操控LSTM的运作。

注意每个只把4个向量的某个维度的值丢给某个LSTM,但是所有的Cell是可以共同一起被运算的。
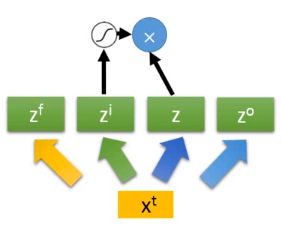
我们知道 z z z要乘上 z i z^i zi通过激活函数的结果,我们上面画出来。
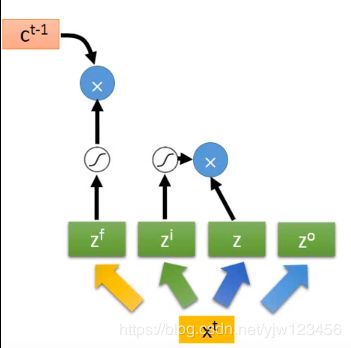
z f z^f zf也要通过遗忘门的激活函数,然后与之前存在Cell中的值相乘(在 c t − 1 c^{t-1} ct−1的某个维度中)。
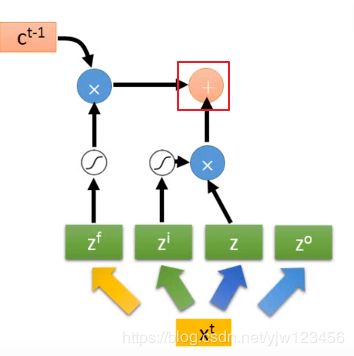
接下来要把上面得到的两个值加起来。

z o z^o zo通过激活函数,把输出与上面的值经过激活函数的结果相乘,最后得到输出 y t y^t yt。
![]()
对了,红框框出来相加后的结果就是存到内存中的值 c t c^t ct。
整个过程会反复进行下去,在下个时间点,输入 x t + 1 x^{t+1} xt+1,然后经过上面一样的过程,得到下个时间点的输出 y t + 1 y^{t+1} yt+1
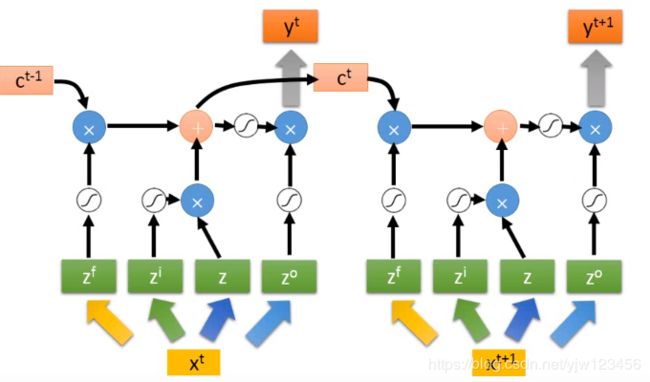
你可能觉得这个很复杂,但这还仅仅是简化的形式,真正的LSTM还会接入一个 h t h^t ht:
把上图红色箭头尾部的输出当做下个时间点的输入。
也就是说下个时间点操控这些门和输入的值不仅仅只是看原来的输入 x t + 1 x^{t+1} xt+1,还会看前一个时间点的输出 h t h^t ht。
其实还不只这样,还会加一个peephole(窥视孔),就是把存在前一个时间点内存中的值也拿出来当成新的时间点的输入。
而且现在随便都会叠个5,6层,它看起来是这样的:

李老师这里还贴出了个图片,类似我看到了什么鬼!?

你可能会觉得这么复杂能否真的有用,但是它还真是很常用的。好在我们用Keras这种工具,可以很方便的开箱即用(上面的没看懂也没关系)。
Keras支持LSTM、GRU(LSTM的简化版,据说表现还差不多,并且不容易过拟合)和SimpleRNN。
参考
1.李宏毅机器学习