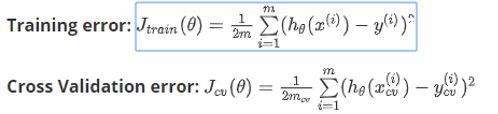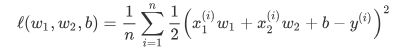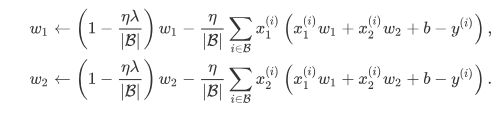动手学深度学习PyTorch版-task3
目录:
task1:https://blog.csdn.net/zahidzqj/article/details/104293563
task2:https://blog.csdn.net/zahidzqj/article/details/104309590
task3:本章节
task4:https://blog.csdn.net/zahidzqj/article/details/104324196
task5:https://blog.csdn.net/zahidzqj/article/details/104324349
task6:https://blog.csdn.net/zahidzqj/article/details/104451810
task8:https://blog.csdn.net/zahidzqj/article/details/104452274
task9:https://blog.csdn.net/zahidzqj/article/details/104452480
task10:https://blog.csdn.net/zahidzqj/article/details/104478668
1.过拟合、欠拟合及其解决方案
基本概念:模型选择、K折交叉验证、过拟合和欠拟合、权重衰减
验证数据集:测试集只能在所有超参数和模型参数选定后使用一次,不可以使用测试数据选择模型,如调参。由于无法从训练误差估计泛化误差,因此也不应只依赖训练数据选择模型。鉴于此,我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证集(validation set)。
K折交叉验证:由于验证数据集不参与模型训练,当训练数据不够用时,预留大量的验证数据显得太奢侈。一种改善的方法是K折交叉验证(K-fold cross-validation)。在K折交叉验证中,我们把原始训练数据集分割成K个不重合的子数据集,然后我们做K次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他K-1个子数据集来训练模型。在这K次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这K次训练误差和验证误差分别求平均。
究模型训练中经常出现的两类典型问题:
- 一类是模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting);
- 另一类是模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。 在实践中,我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题,在这里我们重点讨论两个因素:模型复杂度和训练数据集大小。
以多项式函数拟合为例,多项式项数越多,模型也就越复杂。一阶多项式函数拟合又叫线性函数拟合。
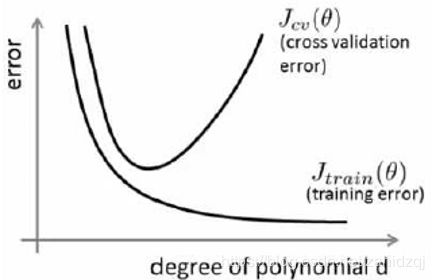
根据训练集和验证集,可以得到两个误差:
对于训练集,当d 较小时,模型拟合程度更低,误差较大;随着 d的增长,拟合程度提高,误差减小。
对于交叉验证集,当 d较小时,模型拟合程度低,误差较大;但是随着d的增长,误差呈现先减小后增大的趋势,转折点是我们的模型开始过拟合训练数据集的时候。
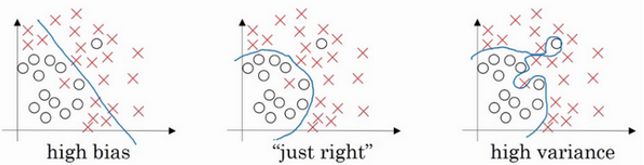
所以,训练集误差和交叉验证集误差近似时:偏差大/欠拟合
交叉验证集误差远大于训练集误差时:方差大/过拟合
过拟合解决方法:
于 L2 范数正则化(regularization):在模型原损失函数基础上添加L2范数惩罚项,从而得到训练所需要最小化的函数。L2范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。
其中w1,w2是权重参数,b是偏差参数。带有L2范数惩罚项的新损失函数为:
其中超参数λ>0。当权重参数均为0时,惩罚项最小。当λ较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当λ设为0时,惩罚项完全不起作用。 有了L2范数惩罚项后,在小批量随机梯度下降中,我们将线性回归一节中权重w1和w2的迭代方式更改为:
可见,L2范数正则化令权重w1和w2先自乘小于1的数,再减去不含惩罚项的梯度。因此,L2范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
问题:为何正则项中只有w,没有b?
因为w通常是一个高维参数矢量,已经可以表达高偏差问题,w可能包含有很多参数,我们不可能拟合所有参数,而b只是单个数字,所以w几乎涵盖所有参数,而不是b,如果加了参数b,其实也没太大影响,因为b只是众多参数中的一个,所以通常省略不计,如果你想加上这个参数,完全没问题。
丢弃法:dropout
假设网络中的每一层,每个节点都以抛硬币的方式设置概率,每个节点得以保留和消除的概率都是0.5,设置完节点概率,我们会消除一些节点,然后删除掉从该节点进出的连线,最后得到一个节点更少,规模更小的网络,然后用backprop方法进行训练。
理解 dropout(Understanding Dropout)
不愿意把所有赌注都放在一个节点上,不愿意给任何一个输入加上太多权重,因为它可能会被删除,因此该单元将通过这种方式积极地传播开,并为单元的四个输入增加一点权重,通过传播所有权重,dropout将产生收缩权重的平方范数的效果,和我们之前讲过的L2正则化类似,实施dropout的结果是它会压缩权重,并完成一些预防过拟合的外层正则化。
dropout被正式地作为一种正则化的替代形式,L2对不同权重的衰减是不同的,它取决于倍增的激活函数的大小。
dropout一大缺点就是代价函数J不再被明确定义,每次迭代,都会随机移除一些节点,如果再三检查梯度下降的性能,实际上是很难进行复查的。定义明确的代价函数 J 每次迭代后都会下降,因为我们所优化的代价函数J实际上并没有明确定义,或者说在某种程度上很难计算,所以我们失去了调试工具来绘制这样的图片。通常会关闭dropout函数,将keep-prob的值设为1,运行代码,确保J函数单调递减。
其他减少神经网络中的过拟合的方法:
1 数据扩增
2 early stopping代表提早停止训练神经网络
2 梯度消失和梯度爆炸
基本概念:消失和爆炸、初始化模型参数、偏移
深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸(explosion)。当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个层数为的多层感知机的第层的权重参数为,输出层的权重参数为。为了便于讨论,不考虑偏差参数,且设所有隐藏层的激活函数为恒等映射(identity mapping)。给定输入,多层感知机的第层的输出。此时,如果层数较大,的计算可能会出现衰减或爆炸。举个例子,假设输入和所有层的权重参数都是标量,如权重参数为0.2和5,多层感知机的第30层输出为输入分别与(消失)和(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
随机初始化模型参数:在神经网络中,通常需要随机初始化模型参数。下面我们来解释这样做的原因:如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值,并传递至输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,无论隐藏单元有多少,隐藏层本质上只有1个隐藏单元在发挥作用。因此,正如在前面的实验中所做的那样,我们通常将神经网络的模型参数,特别是权重参数,进行随机初始化。
PyTorch的默认随机初始化:随机初始化模型参数的方法有很多。在线性回归的简洁实现中,我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过,PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略(不同类型的layer具体采样的哪一种初始化方法的可参考源代码),因此一般不用我们考虑。
Xavier随机初始化:还有一种比较常用的随机初始化方法叫作Xavier随机初始化。 假设某全连接层的输入个数为,输出个数为,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
它的设计主要考虑到,模型参数初始化后,每层输出的方差不该受该层输入个数影响,且每层梯度的方差也不该受该层输出个数影响。
考虑环境因素:协变量偏移、标签偏移、概念偏移
协变量偏移:这里我们假设,虽然输入的分布可能随时间而改变,但是标记函数,即条件分布P(y∣x)不会改变。虽然这个问题容易理解,但在实践中也容易忽视。
想想区分猫和狗的一个例子。我们的训练数据使用的是猫和狗的真实的照片,但是在测试时,我们被要求对猫和狗的卡通图片进行分类。

显然,这不太可能奏效。训练集由照片组成,而测试集只包含卡通。在一个看起来与测试集有着本质不同的数据集上进行训练,而不考虑如何适应新的情况,这是不是一个好主意。不幸的是,这是一个非常常见的陷阱。
统计学家称这种协变量变化是因为问题的根源在于特征分布的变化(即协变量的变化)。数学上,我们可以说P(x)改变了,但P(y∣x)保持不变。尽管它的有用性并不局限于此,当我们认为x导致y时,协变量移位通常是正确的假设。
标签偏移:当我们认为导致偏移的是标签P(y)上的边缘分布的变化,但类条件分布是不变的P(x∣y)时,就会出现相反的问题。当我们认为y导致x时,标签偏移是一个合理的假设。例如,通常我们希望根据其表现来预测诊断结果。在这种情况下,我们认为诊断引起的表现,即疾病引起的症状。有时标签偏移和协变量移位假设可以同时成立。例如,当真正的标签函数是确定的和不变的,那么协变量偏移将始终保持,包括如果标签偏移也保持。有趣的是,当我们期望标签偏移和协变量偏移保持时,使用来自标签偏移假设的方法通常是有利的。这是因为这些方法倾向于操作看起来像标签的对象,这(在深度学习中)与处理看起来像输入的对象(在深度学习中)相比相对容易一些。
病因(要预测的诊断结果)导致 症状(观察到的结果)。
训练数据集,数据很少只包含流感p(y)的样本。
而测试数据集有流感p(y)和流感q(y),其中不变的是流感症状p(x|y)。
概念偏移:另一个相关的问题出现在概念转换中,即标签本身的定义发生变化的情况。事实证明,如果我们周游美国,按地理位置转移数据来源,一个简单术语的定义也会发生相当大的概念转变。
如果我们要建立一个机器翻译系统,分布P(y∣x)可能因我们的位置而异。这个问题很难发现。另一个可取之处是P(y∣x)通常只是逐渐变化。
3 循环神经网络进阶
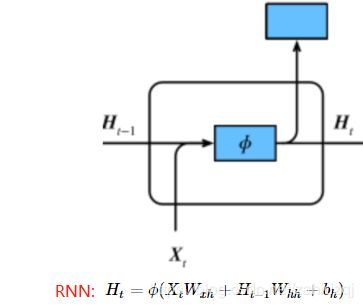
RNN存在的问题:梯度较容易出现衰减或爆炸(BPTT)
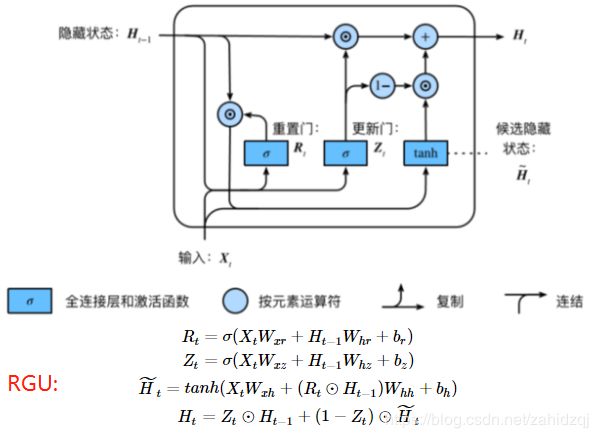
GRU⻔控循环神经⽹络:捕捉时间序列中时间步距离较⼤的依赖关系
GRU的好处: 重置⻔有助于捕捉时间序列⾥短期的依赖关系;
更新⻔有助于捕捉时间序列⾥⻓期的依赖关系。
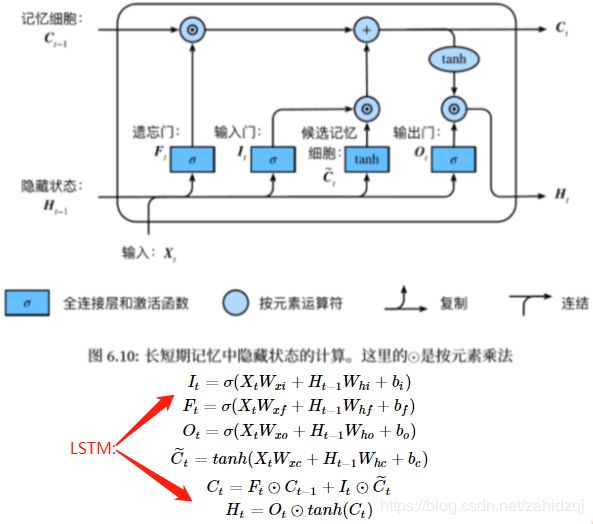
LSTM(long short-term memory):
遗忘门:控制上一时间步的记忆细胞 输入门:控制当前时间步的输入
输出门:控制从记忆细胞到隐藏状态
记忆细胞:⼀种特殊的隐藏状态的信息的流动
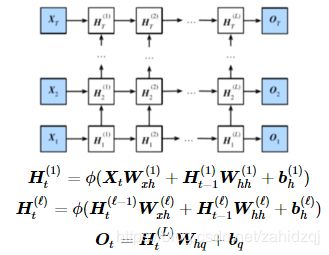
深度循环神经网络:
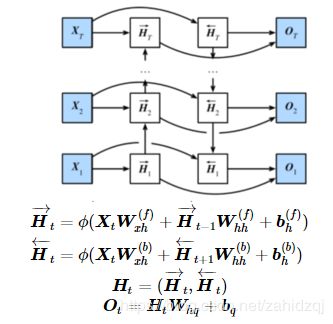
双向循环神经网络: