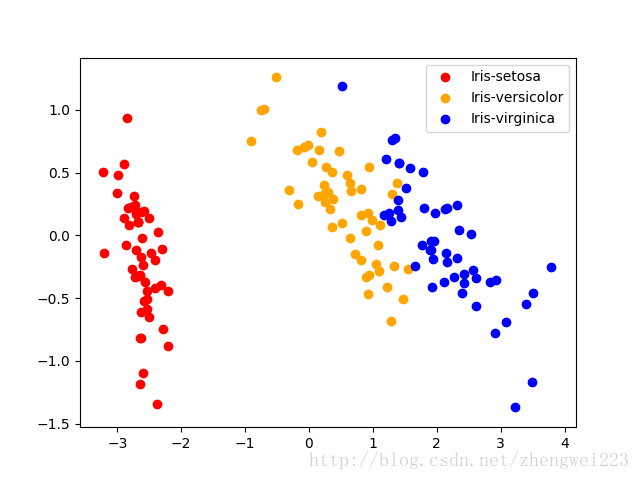
PCA、SVD应用示例：低维投影可视化

数据准备

Iris

Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。

访问http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data下载数据，另存为文件，命名为“iris.data.txt”。

任务描述

该数据有150个样本，每个样本有4个属性，一个目标（即分类结果）。

现在我们希望在一个平面（二维空间）里面把这些样本以点的形式来展现，且将不同类的点标为不同的颜色，用以观察聚合与分散程度。

python代码

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
该数据有150个样本，每个样本有4个属性，一个目标（即分类结果）。

现在我们希望在一个平面（二维空间）里面把这些样本以点的形式来展现，且将不同类的点标为不同的颜色，用以观察聚合与分散程度。
"""

class PCA:
    def __init__(self, dimension, train_x):
        # 降维后的维度
        self.dimension = dimension
        # 原始数据集
        self.train_x = train_x

    @property
    def result(self):
        '返回降维后的矩阵'
        # 1. 数据中心化
        data_centering = self.train_x - np.mean(self.train_x, axis=0)
        # 2. 计算协方差矩阵
        cov_matrix = np.cov(data_centering, rowvar=False)
        # 3. 特征值分解
        eigen_val, eigen_vec = np.linalg.eig(cov_matrix)
        # print(eigen_vec.shape)
        # 4. 生成降维后的数据
        p = eigen_vec[:, 0:self.dimension]  # 取特征向量矩阵的前k维
        return np.dot(data_centering,p)


def load_iris_data():
    '加载鸢尾花数据'
    with open("iris.data.txt", "r") as f:
        iris = []
        for line in f.readlines():
            temp = line.strip().split(",")
            # 将分类转为数字
            if temp[4] == "Iris-setosa":
                temp[4] = 0
            elif temp[4] == "Iris-versicolor":
                temp[4] = 1
            elif temp[4] == "Iris-virginica":
                temp[4] = 2
            else:
                raise (Exception("data error."))
            iris.append(temp)
    iris = np.array(iris, np.float)
    return iris


def draw_result(new_trainX, iris):
    """
    new_trainX:     降维后的数据
    iris:           原数据
    """
    plt.figure()
    # 提取Iris-setosa
    setosa = new_trainX[iris[:, 4] == 0]

    # 绘制点：参数1 x向量，y向量
    plt.scatter(setosa[:, 0], setosa[:, 1], color="red", label="Iris-setosa")

    # Iris-versicolor
    versicolor = new_trainX[iris[:, 4] == 1]
    plt.scatter(versicolor[:, 0], versicolor[:, 1], color="orange", label="Iris-versicolor")

    # Iris-virginica
    virginica = new_trainX[iris[:, 4] == 2]
    plt.scatter(virginica[:, 0], virginica[:, 1], color="blue", label="Iris-virginica")
    plt.legend()
    plt.show()


def main(dimension=2):
    # 这是一个150*5维的矩阵
    iris = load_iris_data()
    # 降到2维，
    pca = PCA(dimension, iris[:, :4])

    # 降维后的数据
    iris_2d = pca.result

    # 降维后的数据可视化
    draw_result(iris_2d, iris)


if __name__ == "__main__":
    main(dimension=2)

SVD实现PCA

class PCA_SVD:
    def __init__(self, dimension, train_x):
        # 降维后的维度
        self.dimension = dimension
        # 原始数据集
        self.train_x = train_x

    @property
    def result(self):
        '返回降维后的矩阵'
        data_centering = self.train_x - np.mean(self.train_x, axis=0)
        # SVD
        U, Sigma, VT = np.linalg.svd(data_centering)
        # print('V==',V)
        return np.dot(data_centering, np.transpose(VT)[:, :self.dimension])

得到的图形是一致的，其实PCA实现中的特征向量矩阵和PCA_SVD实现中VT的转置是一样的。

类似地我们可以到UCI Machine Learning Repository上找些数据集来玩玩。