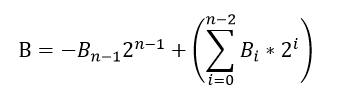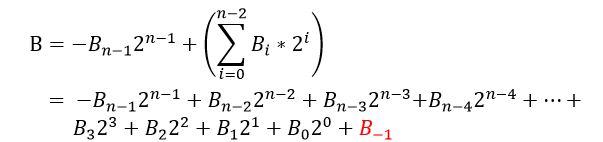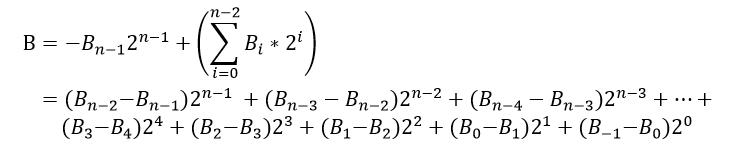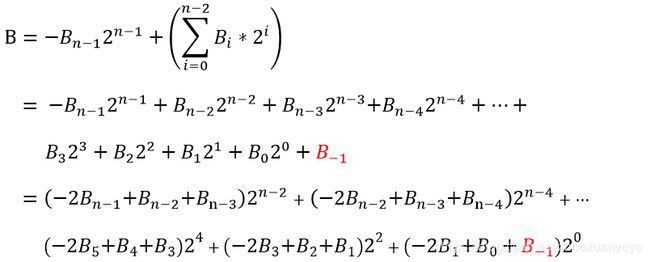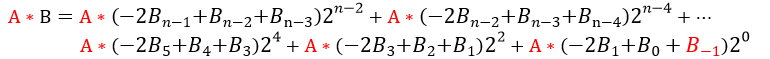【HDL系列】乘法器(6)——Radix-4 Booth乘法器

目录

一、Radix-4 Booth乘法器原理

二、Verilog设计

---

一、Radix-4 Booth乘法器原理

上文中介绍了基2 Booth乘法器，本文继续介绍基4 Booth乘法器。

对于N比特数B来说：

N比特数B，将其展开，其中B-1=0：

基2 Booth表示为：

其基系数为：

基4 Booth乘法器的基系数为：

所以，上式B可以重写为如下式(位宽为偶数)：

将A与B相乘，则：

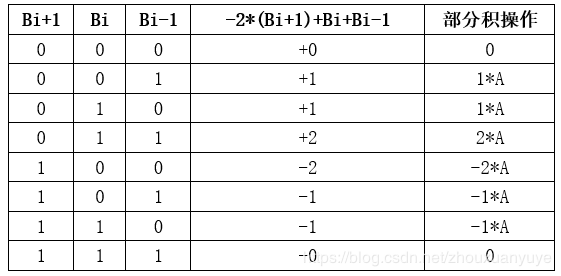
以下是基4 Booth编码表，其中A为被乘数，B为乘数。

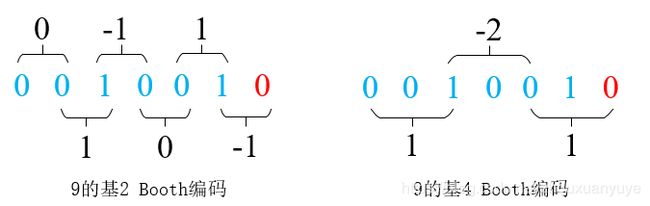
以下为6比特数9的Radix-2 Booth和Radix-4 Booth编码例子：

从基2看9：

9 = 0*2^4 + 1*2^4 + (-1)*2^3 + 0*2^2 + 1*2^1 + (-1)*2^0

从基4看9：

9 = 1*4^2 + (-2)*4^1 + 1*4^0

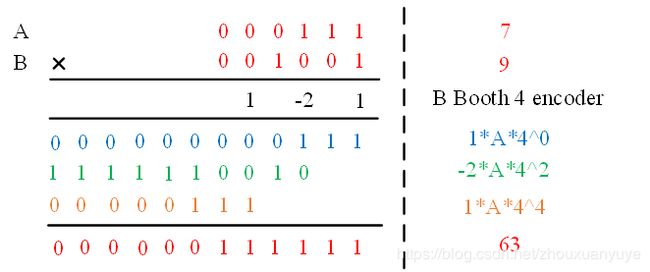
其阵列表示如下：

可以看出，6比特乘数的基2 Booth算法部分累积和个数为6，而基4的部分累积和数为3。

相比于基2 Booth编码，基4 Booth编码将使得乘法累积的部分和数减少一半，其基系数只涉及到移位和补码计算。对于二进制码为1010…1010的乘数（1与0交替），如果采用基2 Booth编码，则部分和累积的输入有几乎一半为被乘数的补码，所以，相比于普通的阵列乘法器，基2 Booth编码的乘法器性能不升反降，基4 Booth编码可以避免以上问题。

 

二、Verilog设计

声明：没有PPA驱动的功能性Verilog设计，仅供娱乐

 

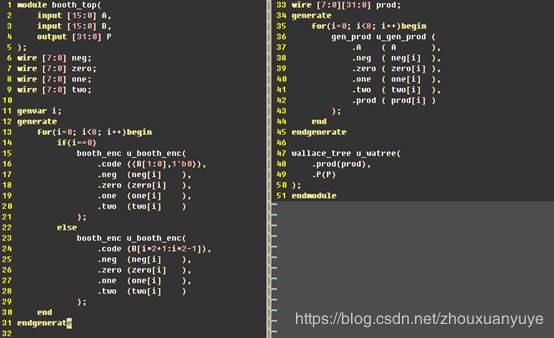
本文中将基于Radix-4 Booth编码、Wallace树、CSA以及行波进位加法器设计一个16比特位宽的有符号数并行阵列乘法器，仅供参考。

几个如下要点：

（1）Wallace树，请参考往期文章《图解Wallace树》；

（2）CSA，请参考往期文章《进位保存加法器原理与设计》；

（3）行波进位加法器，请参考往期文章《半加器、全加器和行波进位加法器原理与设计》；

（4）Radix-4 Booth编码器；

（5）部分和生成。

前3点在往期的文章中已有介绍并设计，所以我们看第（4）点，即一个基4 Booth编码器，根据输入3比特生成0，+1，+2，-2，-1等系数。

根据以上Booth编码表可以将系数生成归纳如下：

假设输入码字为B[2:0]

1.B[2]决定了输出系数的符号位，定义为neg；

2.当输入码字为011和100时，输出绝对值为2，定义为two；

3.当输入码字为000和111时，输出绝对值为0，定义为zero；

4.除了以上码字，输出绝对值为1，定义为one。

基4 Booth编码器

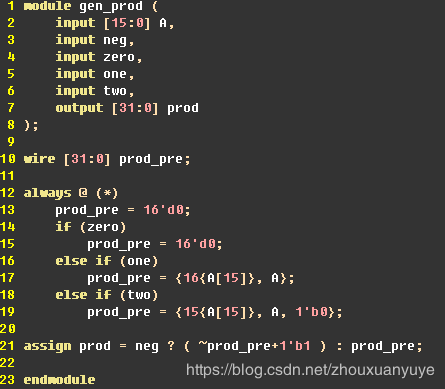
第（5）点生成部分和，根据编码器输出，与被乘数相乘，生成部分和：、

1.如果编码器zero为1，则输出部分和为0；

2.如果编码器one为1，则输出部分和为被乘数；

3.如果编码器two为1，则输出部分和为被乘数左移1位；

4.如果是负数，则生成补码输出。

生成部分和

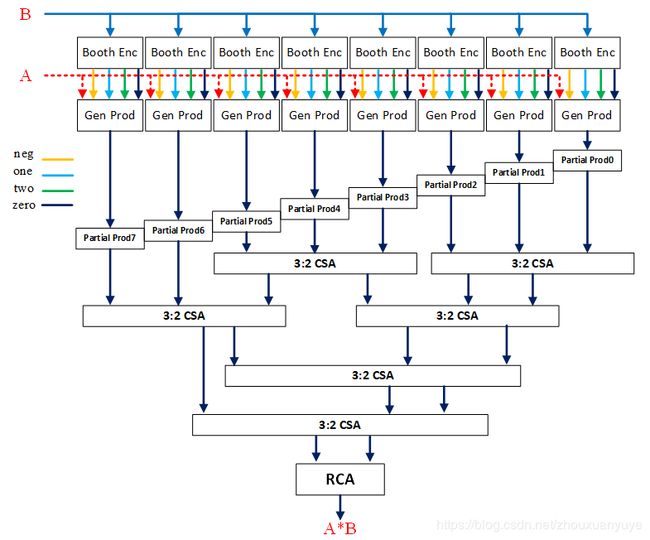
16比特乘法器，需要8个Booth编码器Booth Enc和8个生成部分和Gen Prod模块。根据Wallace树结构、CSA和行波进位加法器RCA，设计框图如下：

Booth乘法器设计框图

Booth乘法器顶层

在追求面积、功耗和速度的要求下，该设计有以下几个优化空间：

（1）部分和生成

    在部分和负数生成中，对于像 “-1*A”和“-2*A”等，进行了取反加一，增大的关键路径延时，且耗费了8个16比特加法器，后期会有改进。

（2）符号位扩展

    在部分和计算中具有大量的符号位扩展，且在求和过程中翻转频繁，故而极大耗费面积和功耗，后期文章会提到；

（3）Wallace树结构

    在Wallace树种求解sum和carry时，简单地进行移位使得3:2 CSA中全加器的位宽为32位，徒增面积和功耗；另外在结构上，因为CSA层次有4级，大概率效率不高，通常还会结合4:2 CSA，后期会提到；

（4）最后一级加法器

    最后一级32比特加法器负责进位链传播，此处是速度最慢的行波进位加法器，可以根据需求进行替换。

（5）流水线技术

    使用流水线技术提升乘法器的性能，

 

根据以上要点设计的基4 Booth乘法器，源码参考公众号回复“011”。

谢谢您的阅读！

原创不易，如果对您有帮助，记得点赞关注哦。欢迎批评指正，谢谢鼓励！

一起“纸上谈芯”，共同学习: