【HDL系列】乘法器(7)——Booth中的符号位扩展技巧

目录

一、无符号乘法符号位扩展原理

二、有符号位乘法符号位扩展原理

三、Verilog设计

---

文介绍了基4 Booth乘法器，并且设计了具有基本功能的Booth乘法器，其中在文末留下了几个有待优化的问题，本文将优化“生成部分和”与“符号位扩展”两部分，参考：https://zhuanlan.zhihu.com/p/143802580

本文原理部分意译自《Sign Extension in Booth Multipliers》，需要说明的是其中的表述存在多处歧义，且Booth编码表负数认定有误，请注意鉴别，其中位宽的问题更值得注意。对于有符号数乘法，其实在用如下符号位扩展时无需自动扩展部分和的符号位，这在参考的文档中是致命的误导，但好在可以通过图片获得该符号位扩展算法的启发。

先给出符号位扩展算法如下（算法有效，已验证）：

    （1）将每个部分和的最高比特位取反；

    （2）对第一个部分和的最高比特位加“1”；

    （3）在所有部分和的最高位前增加1比特数“1”。

依据以上3条规则，我总结为“取反”，“加一”，“再加一”。

以4*4有符号乘法器为例，A=4‘b1111=-1，B=4‘b0100=4，P=A*B=-4，如下图为使用符号位扩展技巧前后的阵列式：

图1. 符号位扩展技巧

上图中（1），仅仅将每一部分的符号位进行扩展，之后按列相加；而在（2）中使用符号位扩展技巧，将不必对每一个部分和进行符号位扩展，首先对部分和符号位取反，然后在第一个部分符号位加1，最后在每个部分和前加1，按列相加即可，得到结果与之前的结果相同。

对于以上4比特位宽有符号数相乘，符号位扩展技术带来的受益不多，但对于多比特数相乘且部分和较多的情况下可以节省大量的面积和功耗，同时对于后级的Wallace，也可以使用更少的CSA。

如果你对以上方法好奇的话，可以从以下一二部分获得一些启发。

一、无符号乘法符号位扩展原理

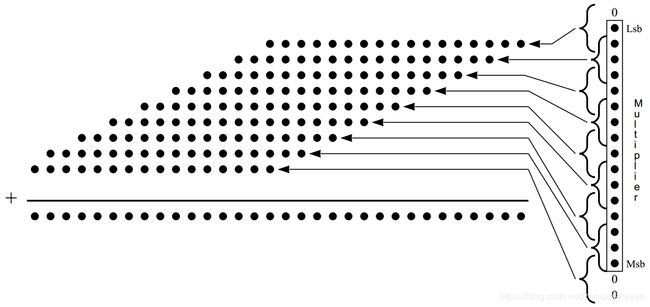
假设16*16无符号乘法器的所有部分和均为正数，如图2所示。在基4 Booth编码中有乘2操作，所以除了底部的部分和为16比特，其他部分和的位宽均为17比特。无符号乘数需在高位补充2位以确保得到一个正的部分和，所以最底部的部分和始终为正，且其位宽为16比特。

图2. 基4 Booth部分和全为正的阵列图

图3表示部分和全为负数，以二进制补码形式表示，最低比特加1。由于被乘数是无符号数，所以乘数的booth编码为负数。

图3. 基4 Booth部分和全为负的阵列图

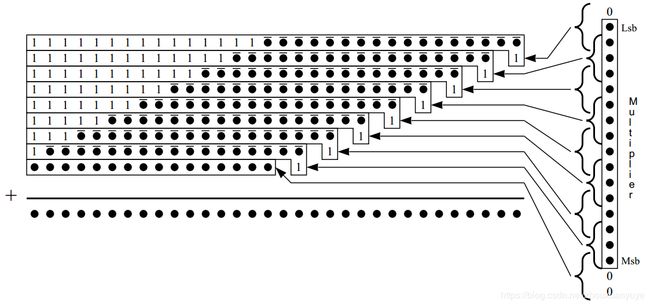
将图3中左上角扩展的符号位全部相加，可以得到如图4所示。

图4. 基4 Booth部分和全为负，扩展位求和结果

假设其中某个部分和不是负数，则该部分和末尾加1的操作将会使连续的1被变换回连续的0。而实际上末尾加1只发生在乘数和与负数相乘的时候，即booth编码为100,101,110的时候。图5显示了这种做法，S表示当前部分和的符号（注意：因为是无符号数相乘，所以此处部分和的符号由booth编码决定，也就是说S是booth码的符号）。

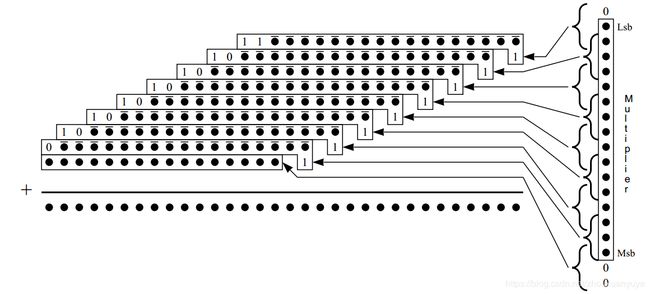
当S=0时，即符号和为正数，最低位不会加1；

当S=1时，即符号位为负数，最低为加1，即对被乘数取反后的加1。

图5. 无符号数乘法，基4 Booth乘法阵列

对S取反的操作加入到第一部分和上，可以减少部分和的个数，降低列高。

当S=0时，~S=1，第一个部分和的最高3比特位100；

当S=1时，~S=0，第一个部分和的最高3比特位001；

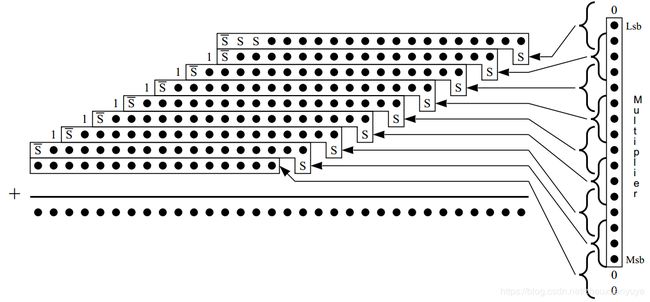
所以变换后的结果如图6所示：

图6. 无符号数乘法，基4 Booth乘法阵列，降低列高

 

二、有符号位乘法符号位扩展原理

基于以上无符号乘法，以下是几点对于有符号乘法需要修改的。

（1）最底部的部分和，在无符号数乘法中用于保证结果是正数，对于有符号乘法是不需要的。对于16*16有符号乘法器，相比无符号乘法器减少一个部分和。

（2）当Booth乘法表选择+Multiplicand或者-Multiplicand时，部分和的第17比特是被乘数的符号位扩展，且该扩展发生在求补码前。

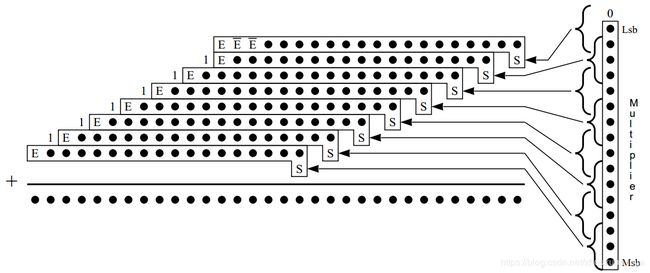
（3）在假设部分和全为负数时，扩展位中连续1的清除与之前稍有不同。当部分和为0是时，部分和中连续的1可以被还原为连续的0。对于有符号数乘法发生在以下情况：被乘数与Booth编码同符号即可。被乘数的符号和乘数编码符号使用同或符号，产生信号“E”，用于当部分和为0时清除假设的连续1。

图7. 16*16有符号乘法阵列

 

三、Verilog设计

本文中将在基于上期文章设计的Booth乘法器（基4 Booth编码、Wallace树、CSA以及行波进位加法器，16比特位宽，有符号数乘法）中使用符号位扩展技巧，以节省符号位扩展带来的不必要的面积和功耗消耗，同时将省去生成部分和中的加法器，仅供参考。

图8是符号位扩展方法，限定8个部分和的位宽大小，不再采用之前固定的32位位宽。

同时修改上期中Booth编码表，只限定编码为100,101,110为负数，neg=1，其他编码neg为0。如果乘数的编码为负数，对被乘数取反后的加1操作将与下个部分和末尾结合成新的部分和。另外，二维数组端口请使用支持sv的综合器。

图8. 符号位扩展方法

 

图9.更新Booth top顶层

 

图10. 随机验证测试结果打印

 

谢谢您的阅读！

原创不易，如果对您有帮助，记得点赞关注哦。欢迎批评指正，谢谢鼓励！

一起“纸上谈芯”，共同学习: