卷积码(Convolutional Code)
卷积码(Convolutional Code)
本文主要简单介绍了卷积码。
关键词:卷积码 生成多项式 网格图 状态图
==============================================================
目录结构:
1、卷积码简介
2、卷积码表示方法
2.1 生成多项式
2.2 状态图
2.3 网格图
3、总结
==============================================================
1、卷积码简介
卷积码是一种差错控制编码,由P.Elias于1955年发明。因为数据与二进制多项式滑动相关故称卷积码。卷积码在通信系统中应用广泛,如IS-95,TD-SCDMA,WCDMA,IEEE 802.11及卫星等系统中均使用了卷积码。
卷积码使用(n,k,L)表示,码率为R。
n为输出码字;
k为输入的比特信息;
L为约束长度,也称为记忆深度。
R表示为R = k/n。
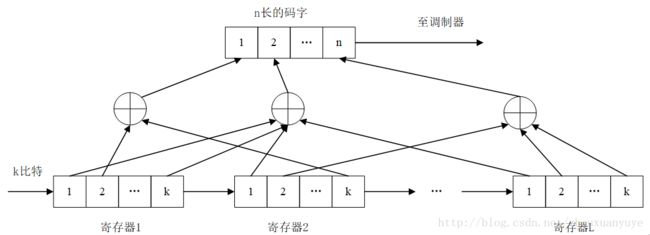
卷积码是一种有记忆的纠错码,编码规则是将k个信息比特编码形成n个比特,编码后的n个码元不但与当前输入的k个信息有关,仍与之前的L-1组的信息有关,其结构如下图1所示,图1来自Goldsmith的著作。
图1、(n,k,L)卷积码编码器
图中表示有L级信息比特,每次输入k比特信息,共有k*L个比特,每次输出n个比特信息,可以明显地看出该n个比特信息不仅与当前输入的k个比特信息有关,与之前L-1组信息比特也有关,所以卷积码是有记忆的编码,记忆深度为L。
注:此处与其他常见表示方法不同,此处将输入的比特做了缓存,所以记忆深度不一样,L看寄存器的个数确定。
2、卷积码表示方法
图2是输出码长n=2,记忆深度L为2,输入比特k=1的,(2,1,2)卷积码编码器。用该例说明卷积码的以下几种表示方法。
图2、(2,1,2)卷积码编码器
2.1 生成多项式
生成多项式使用K-1阶的多项式描述编码器的移位寄存器和模二加法器的连接状态。每个模二加法器的连接可表示成一个多项式。多项式的次数输入的阶次为0,其余按寄存器数的移位次数依次递增。如上图
输出1: g1(x) = 1 + x + x^2
输出2: g2(x) = 1 + x^2
以下是IEEE 802.11标准中的卷积码编码器,生成多项式分别为:
输出1: g1(x) = 1 + x^2 + x^3+ x^5 + x^6
输出2: g2(x) = 1 + x + x^2 +x^3 + x^6
图3、IEEE 802.11中的卷积码编码器
2.2 状态图
状态图是关于系统状态变化的描述,它将由系统的输入,根据当前的系统状态,影响系统的输出。卷积码编码器存储的L-1段消息,既要因新的消息输入而改变,又要影响当前的编码输出,把卷积码编码器的移位寄存器中任一时刻所存储的信息称为卷积码编码器的一个状态。
(n,k,L)卷积码共有2^(k*(L-1))个状态,每次输入k比特只有2^k种状态变化,所以,每个状态只能转移到全部状态的某个子集(2^k个状态)中去,每个状态也只能由全部状态的某个子集(2^k个状态)转移而来。
(2,1,2)卷积码编码器包含2级移位寄存器和2个模2加法器。2级移位寄存器共有2^2=4种不同状态,定义为S0(00)、S1(01)、S2(10)和S3(11)四种状态。在每个时刻,输入的1个比特信息,当前状态将转为4种状态中的任何一种。
表1、卷积码的状态转移表
输入 |
当前状态 |
下个状态 |
输出1 |
输出2 |
0 |
00 |
00 |
0 |
0 |
0 |
01 |
00 |
1 |
1 |
0 |
10 |
01 |
1 |
0 |
0 |
11 |
01 |
0 |
1 |
1 |
00 |
10 |
1 |
1 |
1 |
01 |
10 |
0 |
0 |
1 |
10 |
11 |
0 |
1 |
1 |
11 |
11 |
1 |
0 |
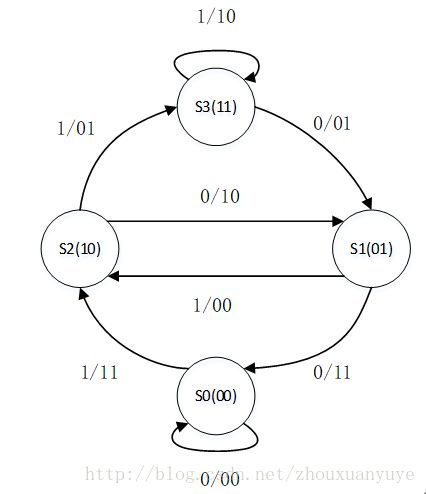
状态表类似查找表,原理即根据当前的输入和当前的状态,可以从表中查得输出信息。图4为卷积码的状态转移图,图中的状态转移表示“输入/输出1输出2”。
图4、(2,1,2)卷积码状态转移图
2.3 网格图
卷积编码器的状态图只能描述某个时刻的状态转移和编码过程,但整个编码的过程是随时间不断变化的过程。为了建立时间与状态转移的关系,将状态图按时间顺序连接,于是形成了卷积码的网格图。
图5、(2,1,2)卷积码的网格图
每一个动态编码的过程都可以用网格图中的一条路径表示,根据以下例子理解网格图,网格图不仅是表示卷积码的一种有效方法,更是理解卷积码译码的关键之处。
如编码序列“0 1 1 0 0”在图中的序列如下:
图6、卷积码编码路径示意图
每次转移的输出依次为00 11 01 01 11,该输出已于图中标记。
3. 总结
本文主要介绍了卷积码的表示及其表示方法多项式表示法,状态转移图法和网格图法。