优化方法:原问题和拉格朗日对偶问题(primal-dual)
本文主要讲解有关原问题和拉格朗日对偶问题,以及它们之间的关系,从而引出弱对偶性和强对偶性以及 KKT 条件和 Slater 条件。
原问题
优化问题一般都可以写为下面的形式:
min f 0 ( x ) , x ∈ R n \min f_0(x),\quad x\in R^n minf0(x),x∈Rn
s . t . f i ( x ) ≤ 0 , i = 1 , 2 , . . . , m s.t.\quad f_i(x)\leq0,\quad i=1,2,...,m s.t.fi(x)≤0,i=1,2,...,m
h j ( x ) = 0 , j = 1 , 2 , . . . , p \quad \quad h_j(x)=0,\quad j=1,2,...,p hj(x)=0,j=1,2,...,p
以上形式被成为原问题,即求解一个满足 m 个不等式约束和 p 个等式约束的函数 f 0 ( x ) f_0(x) f0(x) 的最小值。实际上我们并不关心最小值是什么,而是关心最小值在 x 是什么的时候取得。
上述是一般的优化问题,而凸优化问题在以上形式的基础上多了几个限制条件:1. f i ( x ) f_i(x) fi(x) 为凸函数 2. h j ( x ) h_j(x) hj(x) 为仿射函数。将一般的优化问题转化为凸优化问题的好处是凸优化只有一个极小值点,也就是说凸优化问题的局部最优解即全局最优解。下面的讨论如果不加以说明都是针对一般的优化问题来说的。
拉格朗日函数
解决带约束的条件的优化问题的一般解决办法是拉格朗日乘子法,也就是先写出拉格朗日函数,再让拉氏函数对 x 求导得到导数为 0 的点,将这些点带入原函数,则其中的最大值即为原函数的最大值,最小值即为原函数的最小值。上述凸优化问题的拉氏函数为:
L ( x , u , v ) = f 0 ( x ) + ∑ i = 1 m u i f i ( x ) + ∑ j = 1 p v j h j ( x ) L(x,u,v)=f_0(x)+\sum_{i=1}^mu_if_i(x)+\sum_{j=1}^pv_jh_j(x) L(x,u,v)=f0(x)+i=1∑muifi(x)+j=1∑pvjhj(x)
其中 u i ≥ 0 u_i\geq0 ui≥0, v j ∈ R v_j\in R vj∈R,这是因为在可行域内,因为 f i ( x ) ≤ 0 f_i(x)\leq0 fi(x)≤0,所以当 u i ≥ 0 u_i\geq0 ui≥0 时, ∑ i = 1 m u i f i ( x ) \sum_{i=1}^mu_if_i(x) ∑i=1muifi(x) 的最大值为 0;因为 h j ( x ) = 0 h_j(x)=0 hj(x)=0,所以 ∑ j = 1 p v j h j ( x ) \sum_{j=1}^pv_jh_j(x) ∑j=1pvjhj(x) 恒为0, v j v_j vj 可以取任意值。这样就保证了 L ( x , u , v ) L(x,u,v) L(x,u,v) 的最大值为原函数 f 0 ( x ) f_0(x) f0(x) ,即 max u , v L ( x , u , v ) = f 0 ( x ) \max_{u,v} L(x,u,v)=f_0(x) maxu,vL(x,u,v)=f0(x)。
对于固定的 x 来说,拉氏函数 L ( x , u , v ) L(x,u,v) L(x,u,v) 为 u u u 和 v 的仿射函数。
拉格朗日对偶函数
由此一来,就把原来的求解带约束条件的原函数转换为了不带约束条件的拉格朗日函数。求解 min x f 0 ( x ) \min_x f_0(x) minxf0(x) 就等价于求解 min x max u , v L ( x , u , v ) \min_x\max_{u,v}L(x,u,v) minxmaxu,vL(x,u,v)。但是该式子并不容易求解,所以引入了拉格朗日对偶函数(注意不是对偶问题),拉格朗日对偶函数就是拉格朗日函数关于 x 取最小值,即:
g ( u , v ) = inf x ∈ D L ( x , u , v ) = inf x ∈ D [ f 0 ( x ) + ∑ i = 1 m u i f i ( x ) + ∑ j = 1 p v j h j ( x ) ] g(u,v)=\inf_{x\in D}L(x,u,v)=\inf_{x\in D}[f_0(x)+\sum_{i=1}^mu_if_i(x)+\sum_{j=1}^pv_jh_j(x)] g(u,v)=x∈DinfL(x,u,v)=x∈Dinf[f0(x)+i=1∑muifi(x)+j=1∑pvjhj(x)]
其中 inf x ∈ D \inf_{x\in D} infx∈D 表示函数逐点对 x 求下确界,也就是对任意的 u u u 和 v 求出一个使得 L ( x , u , v ) L(x,u,v) L(x,u,v) 最小的 x 。当拉氏函数没有下确界时,定义下确界为 − ∞ -\infty −∞,即 g ( u , v ) = − ∞ g(u,v)=-\infty g(u,v)=−∞; D 是可行域。拉格朗日对偶函数是一个凹函数,也就是说它存在一个唯一的极大值点。
拉氏对偶函数为凹函数证明
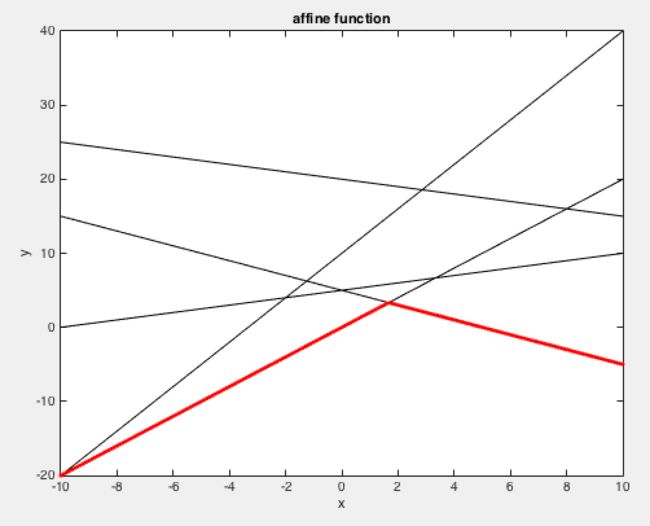
先来感性的看一下这个问题,因为是拉氏对偶函数是关于 u 和 v 的仿射函数,所以可以用下面两张示意图表示对 x 逐点取最小值的结果:
上图是随便画的多个仿射函数,对其逐点取最小值得到下图:
可以发现结果是一个凹函数。
拉氏对偶函数和原函数的关系
因为 min x f 0 ( x ) = min x max u , v L ( x , u , v ) ≥ max u , v min x L ( x , u , v ) = m a x u , v g ( u , v ) \min_x f_0(x)=\min_x\max_{u,v}L(x,u,v)\geq\max_{u,v}\min_xL(x,u,v)=max_{u,v}g(u,v) minxf0(x)=minxmaxu,vL(x,u,v)≥maxu,vminxL(x,u,v)=maxu,vg(u,v),所以可以用拉格朗日对偶的最大值去逼近原函数的最小值。下面来证明一下上面式子的正确性:
因为任何函数都不大于其对某个变量求最大值,故:
f ( x , y ) ≤ max x f ( x , y ) f(x,y)\leq\max_x f(x,y) f(x,y)≤xmaxf(x,y)
上式两边对 y 求最小值得:
min y f ( x , y ) ≤ min y max x f ( x , y ) \min_yf(x,y)\leq\min_y\max_x f(x,y) yminf(x,y)≤yminxmaxf(x,y)
上式中不等式的前面是一个关于 x 的函数,不妨记为 G(x),不等式后面是一个定值,不妨记为 A,所以说 G ( x ) ≤ A G(x)\leq A G(x)≤A,所以 G(x) 的最大值也不大于 A:
max x min y f ( x , y ) ≤ min y max x f ( x , y ) \max_x\min_yf(x,y)\leq\min_y\max_x f(x,y) xmaxyminf(x,y)≤yminxmaxf(x,y)
得证。
弱对偶和强对偶
我们用 p ∗ p^* p∗ 表示原问题的最优解,即 p ∗ = min x f 0 ( x ) p^*=\min_xf_0(x) p∗=minxf0(x);用 d ∗ d^* d∗ 表示拉氏对偶函数的最优解,即 d ∗ = max u , v g ( u , v ) d^*=\max_{u,v}g(u,v) d∗=maxu,vg(u,v)。并定义原问题的最优解与拉氏对偶问题的最优解之间的差值为 对偶间隙(dual gap),即 p ∗ − d ∗ p^*-d^* p∗−d∗。
前面我们已经证明了原问题的最优解大于等于对偶问题的最优解,即 p ∗ ≥ d ∗ p^*\geq d^* p∗≥d∗,这个性质被称作 弱对偶性 ,也可以表示为对偶间隙大于等于 0,即 p ∗ − d ∗ ≥ 0 p^*-d^*\geq 0 p∗−d∗≥0。即使当 p ∗ p^* p∗ 和 d ∗ d^* d∗ 无限时,弱对偶性仍然成立。如果原问题无下界,则对偶问题也无下界;如果对偶问题无上界,则原问题也无上界,即原问题不可行。
如果原问题的最优解和拉氏对偶问题的最优解相等,也就是对偶间隙为 0,则 强对偶性 成立。
一般情况下强对偶性不成立,但是如果原问题是凸优化问题,即原函数和不等式约束 f i ( x ) f_i(x) fi(x) 为凸函数,而等式约束 h j ( x ) h_j(x) hj(x) 为仿射函数,则强对偶性通常(但不总是)成立。而强对偶性成立的条件一般被称为 约束准则。下面主要讲解两个约束准则—— KKT 条件 和 Slater 条件。
KKT 条件
之前证明了我们可以用拉格朗日对偶的最大值去逼近原函数的最小值的思路是正确的,但是什么时候两者的最大值和最小值相等呢?
首先假设函数 f 0 ( x ) , . . . , f m ( x ) , h 1 ( x ) , . . . , h p ( x ) f_0(x),...,f_m(x),h_1(x),...,h_p(x) f0(x),...,fm(x),h1(x),...,hp(x) 都可微,但并不假设这些函数为凸函数,则拉氏对偶函数:
g ( u ∗ , v ∗ ) = inf x [ f 0 ( x ) + ∑ i = 1 m u i ∗ f i ( x ) + ∑ j = 1 p v j ∗ h j ( x ) ] g(u^*,v^*)=\inf_x[f_0(x)+\sum_{i=1}^mu_i^*f_i(x)+\sum_{j=1}^pv_j^*h_j(x)] g(u∗,v∗)=xinf[f0(x)+i=1∑mui∗fi(x)+j=1∑pvj∗hj(x)]
因为一个函数的下确界(最小值)不大于函数本身,故:
≤ f 0 ( x ∗ ) + ∑ i = 1 m u i ∗ f i ( x ∗ ) + ∑ j = 1 p v j ∗ h j ( x ∗ ) \leq f_0(x^*)+\sum_{i=1}^mu_i^*f_i(x^*)+\sum_{j=1}^pv_j^*h_j(x^*) ≤f0(x∗)+i=1∑mui∗fi(x∗)+j=1∑pvj∗hj(x∗)
又因为后两项的最大值为 0,故:
≤ f 0 ( x ∗ ) \leq f_0(x^*) ≤f0(x∗)
上面三式中, u ∗ u^* u∗、 v ∗ v^* v∗ 和 x ∗ x^* x∗ 分别是拉格朗日对偶函数和原函数的最优解。所以说要想让拉格朗日对偶函数的最大值和原函数最小值相等,需要让上面三式中的小于等于号全部取等号。
因为拉格朗日函数在 x ∗ x^* x∗ 处取得极小值,因此拉氏函数在 x ∗ x^* x∗ 处的导数为 0 。所以第一个 ≤ \leq ≤ 取等号的条件是拉氏函数对 x ∗ x^* x∗ 的偏导为 0,即:
∇ f 0 ( x ∗ ) + ∑ i = 1 m u i ∗ ∇ f i ( x ) + ∑ j = 1 p v j ∗ ∇ h j ( x ) = 0 条 件 ( 1 ) \nabla f_0(x^*)+\sum_{i=1}^mu_i^*\nabla f_i(x)+\sum_{j=1}^pv_j^*\nabla h_j(x)=0\quad\quad\quad\quad 条件 (1) ∇f0(x∗)+i=1∑mui∗∇fi(x)+j=1∑pvj∗∇hj(x)=0条件(1)
第二个 ≤ \leq ≤ 取等号的条件是 ∑ i = 1 m u i ∗ f i ( x ∗ ) \sum_{i=1}^mu_i^*f_i(x^*) ∑i=1mui∗fi(x∗) 和 ∑ j = 1 p v j ∗ h j ( x ∗ ) \sum_{j=1}^pv_j^*h_j(x^*) ∑j=1pvj∗hj(x∗) 全部为 0,前面说了,后者恒等于 0,而前者为 0 的条件是:
∑ i = 1 m u i ∗ f i ( x ∗ ) = 0 \sum_{i=1}^mu_i^*f_i(x^*)=0 i=1∑mui∗fi(x∗)=0
但是因为在可行域内,以上求和项的每一项都是非正的,因此以上条件等价于:
u i ∗ f i ( x ∗ ) = 0 条 件 ( 2 ) u_i^*f_i(x^*)=0\quad\quad\quad\quad\quad\quad\quad条件(2) ui∗fi(x∗)=0条件(2)
以上 2 个约束条件,再加上凸优化问题自身的三个约束条件就得到了著名的 KKT 条件,和 KMP 算法的名称类似,所谓的 KKT 条件的命名其实是三位科学家名字的英文首字母的组合,KKT 条件即:
f i ( x ∗ ) ≤ 0 , i = 1 , . . . , m f_i(x^*)\leq0,\quad i=1,...,m fi(x∗)≤0,i=1,...,m
h i ( x ∗ ) = 0 , i = 1 , . . . , p h_i(x^*)=0,\quad i=1,...,p hi(x∗)=0,i=1,...,p
u i ∗ ≥ 0 , i = 1 , . . . , m u_i^*\geq0,\quad i=1,...,m ui∗≥0,i=1,...,m
∇ f 0 ( x ∗ ) + ∑ i = 1 m u i ∗ ∇ f i ( x ) + ∑ j = 1 p v j ∗ ∇ h j ( x ) = 0 \nabla f_0(x^*)+\sum_{i=1}^mu_i^*\nabla f_i(x)+\sum_{j=1}^pv_j^*\nabla h_j(x)=0 ∇f0(x∗)+i=1∑mui∗∇fi(x)+j=1∑pvj∗∇hj(x)=0
u i ∗ f i ( x ∗ ) = 0 u_i^*f_i(x^*)=0 ui∗fi(x∗)=0
KKT 条件中的条件 (2) u i ∗ f i ( x ∗ ) = 0 u_i^*f_i(x^*)=0 ui∗fi(x∗)=0 也被成为 互补松弛性,我们可以将互补松弛条件等价地改写为:
u i ∗ > 0 ⇒ f i ( x ∗ ) = 0 u_i^*>0\Rightarrow f_i(x^*)=0 ui∗>0⇒fi(x∗)=0
或者:
f i ( x ∗ ) < 0 ⇒ u i ∗ = 0 f_i(x^*)<0\Rightarrow u_i^*=0 fi(x∗)<0⇒ui∗=0
这是因为在可行域内有 u i ∗ ≥ 0 u_i^*\geq 0 ui∗≥0 并且 f i ( x ∗ ) ≤ 0 f_i(x^*)\leq 0 fi(x∗)≤0。
Slater 条件
如果原始问题为凸优化问题,并且存在一点 x 使得所有的约束条件都小于 0,即:
f i ( x ) < 0 , i = 1 , . . . , m f_i(x)<0,\quad i=1,...,m fi(x)<0,i=1,...,m
则强对偶性成立。
上述条件就是所谓的 Slater 条件,而满足上述条件的点被称为 严格可行,这是因为不等式约束严格成立。
当不等式约束函数 f i ( x ) f_i(x) fi(x) 中有一些函数是仿射函数时,Slater 条件可以进一步改进。我们假设前 k 个不等式约束函数为仿射函数,则强对偶性成立的条件(即改进后的 Slater 条件)为:存在一点 x 使得前 k 个不等式约束函数小于等于 0,而其他不等式约束函数小于 0,即
f i ( x ) ≤ 0 , i = 1 , . . . , k f_i(x)\leq 0,\quad i=1,...,k fi(x)≤0,i=1,...,k
f i ( x ) < 0 , i = k + 1 , . . . , m f_i(x)<0,\quad i=k+1,...,m fi(x)<0,i=k+1,...,m
换句话说,仿射函数不等式不需要严格成立。