| Introduction In this lab, we learnt the principles of Multiple-Input-Multiple-Output (MIMO) systems, which use multiple antennas at the transmitter and receiver ends of a wireless communication system. MIMO systems are increasingly being adopted in communication systems for the potential gains in capacity they realize when using multiple antennas. Multiple antennas use the spatial dimension in addition to the time and frequency ones, without changing the bandwidth requirements of the system. To achieve the higher capacity which is close to Shannon capacity (C=Blog_2 (1+SNR)), we need a lot of method to decrease BER, space time code is a method. It is assumed here that the channel undergoes independent fading between the multiple transmit-receive antenna pairs. Space–time block coding combines all the copies of the received signal in an optimal way to extract as much information from each of them as possible. The data are constructed as a matrix which has its columns equal to the number of the transmit antennas and its rows equal to the number of the time slots required to transmit the data. At the receiver side, the signals received are first combined and then sent to the maximum likelihood detector where the decision rules are applied. Space-time block codes were designed to achieve the maximum diversity order for the given number of transmit and receive antennas subject to the constraint of having a simple linear decoding algorithm. This has made space-time block codes a very popular and most widely used scheme. In this lab, we mainly care the Alamouti scheme which can achieve diversity gain is 2 when CSIT isn’t known and the number of transmit antennas is 2. Theoretical knowledge: Alamouti scheme is the basis of the Space Time Coding technique. The mathematical explanation of the scheme with two transmitting and one receiving antenna is also explained here. In this work, a two-branch transmit diversity scheme is implemented. Using two transmit antennas and one receive antenna, the scheme provides the same diversity order as maximal-ratio receiver combining (MRRC) with one transmit antenna and two receive antennas. At the transmitter side, a block of two symbols is taken from the source data and sent to the modulator. After that, Alamouti space-time encoder takes the two modulated symbols, in this case called s1 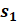 and s2 and s2 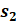 creates encoding matrix S creates encoding matrix S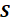 where the symbols s1 where the symbols s1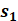 and s2 and s2 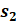 are mapped to two transmit antennas in two transmit time slots. The encoding matrix is given by: are mapped to two transmit antennas in two transmit time slots. The encoding matrix is given by: S=s1-s2*s2s1*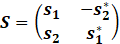 In receive antenna, we can get: r1=h1s1+h2s2+n1r2=-h1s2*+h2s1*+n2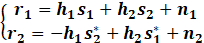 We can convert above equations to a matrix operation: r1r2*=h1h2h2*-h1*s1s2+n1n2*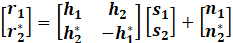 We defined: r=r1r2* S=s1s2 n=n2n2* H=h1h2h2*-h1* 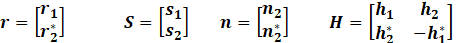 We can get: r=HS+n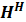 Then, we use HH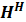 multiplex above equation: multiplex above equation: HHr=S+HHn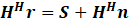 Then, we can get: h1*h2h2*-h1r1r2*=(h12+h22)s1s2+h1*n1h2n2*h2*n1-h1n2*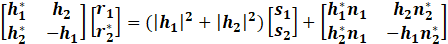 So, by this way, even if we don’t know the CSIT, we can use Alamouti scheme to achieve diversity gain is 2. The slope of BER with SNR become larger. Lab results & Analysis: First, we can try to achieve the example ‘Introduction to MIMO Systems’ in Communications System Toolbox . . The results are shown in these two figures: ![[通信系统设计]Lab3 MIMO Programming_第1张图片](http://img.e-com-net.com/image/info8/aa7ca297f37f4d7ea87783a8741d61e0.jpg) ![[通信系统设计]Lab3 MIMO Programming_第2张图片](http://img.e-com-net.com/image/info8/3f99b20671534b48ac8da8d2c8811e81.jpg)
Figure 1 The results of the Introduction to MIMO Systems Then we can start completing the question of this lab: The steps of MATLAB script performs the following:
- Generate random binary sequence of +1′s and -1′s.
- Group them into pair of two symbols
- Code it per the Alamouti Space Time code, multiply the symbols with the channel.
- Equalize the received symbols
- Perform hard decision decoding and count the bit errors
- Repeat for multiple values of EBN0
 and plot the simulation and theoretical results. and plot the simulation and theoretical results.
Question one: Implement Alamouti 2X1 and 2X2 simulation (QPSK and 16QAM) ![[通信系统设计]Lab3 MIMO Programming_第3张图片](http://img.e-com-net.com/image/info8/a419be9da76448ab8d25c8595458f9b4.jpg)
The key part of the MATLAB codes of question one are shown: Alamouti STBC
| sCode = zeros(2,N); sCode(:,1:2:end) = (1/sqrt(2))*reshape(s,2,N/2); % [x1 x2 ...] sCode(:,2:2:end)=(1/sqrt(2))*(kron(ones(1,N/2),[-1;1]).*flipud(reshape(conj(s),2,N/2))); % [-x2* x1* ....] h = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; % Rayleigh channel hMod = kron(reshape(h,2,N/2),ones(1,2)); % repeating the same channel for two symbols n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; % white gaussian noise, 0dB variance |
Forming the equalization matrix by using the formula: ![[通信系统设计]Lab3 MIMO Programming_第4张图片](http://img.e-com-net.com/image/info8/974a528be3a74f458720a38e0f5ead72.png)
| hEq = zeros(2,N); hEq(:,[1:2:end]) = reshape(h,2,N/2); % [h1 0 ... ; h2 0...] hEq(:,[2:2:end]) = kron(ones(1,N/2),[1;-1]).*flipud(reshape(h,2,N/2)); % [h1 h2 ... ; h2 -h1 ...] hEq(1,:) = conj(hEq(1,:)); % [h1* h2* ... ; h2 -h1 .... ] hEqPower = sum(hEq.*conj(hEq),1); yHat = sum(hEq.*yMod,1)./hEqPower; % [h1*y1 + h2y2*, h2*y1 -h1y2*, ... ] yHat(2:2:end) = conj(yHat(2:2:end)); |
Then should change message to ['Hello world 0000','Hello world 0001','Hello world 0002','Hello world 0003','Hello world 0004','Hello world 0005','Hello world 0006'…]. The results are shown in these figures: ![[通信系统设计]Lab3 MIMO Programming_第5张图片](http://img.e-com-net.com/image/info8/a337e343a2e84cc69d3616e9db5b3a92.jpg)
Figure 2 the relationship between BER and EBN0 By obverting the results of this question, we can find that when EBN0 and modulation method are same, BER of the 2*2 is smaller than 2*1. Compared to the BER plot for nTx=2, nRx=1, we can see the Alamouti Space Time Block Coding has around 3dB poorer performance. This is because the effective channel concatenating the information from 2 receive antennas over two symbols results in a diversity order of 4. In general, with m receive antennas, the diversity order for 2 transmit antenna Alamouti STBC is 2m receive antennas, the diversity order for 2 transmit antenna Alamouti STBC is 2m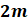 . As with the case of 2 transmit, 1 receive Alamouti STBC, the fact that HHH . As with the case of 2 transmit, 1 receive Alamouti STBC, the fact that HHH is a diagonal matrix ensured that there is no cross talk between , after the equalizer and the noise term is still white. is a diagonal matrix ensured that there is no cross talk between , after the equalizer and the noise term is still white. We can compare the result we got with the figure mentioned in this paper “BER Analysis of Alamouti Space Time Block Coded 2x2 MIMO Systems using Rayleigh Dent Mobile Radio Channel” ![[通信系统设计]Lab3 MIMO Programming_第6张图片](http://img.e-com-net.com/image/info8/727ce17553344b92ba079858b9877980.jpg)
We can find that the extension of our result is as same as the results in this paper which indicates our program and stimulation are successful. Question two: Apply Alamouti 2X2 to the QPSK transceiver In this question, a QPSK modulated Alamouti STBC is simulated over a 2x2 quasi-static frequency-flat Rayleigh channel. The SNR range to be simulated is 0 to 10 dB . The transmitter and receiver have two dipole antenna elements each. The BER vs. EBN0 curves are plotted. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas. The channel experienced between each transmit to the receive antenna is randomly varying in time. However, the channel is assumed to remain constant over two time slots. . The transmitter and receiver have two dipole antenna elements each. The BER vs. EBN0 curves are plotted. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas. The channel experienced between each transmit to the receive antenna is randomly varying in time. However, the channel is assumed to remain constant over two time slots. The key part of the MATLAB codes of question two are shown: Create objects to perform QPSK modulation and demodulation, Alamouti encoding and combining, channel as well as BER calculation.
| qpskMod = comm.QPSKModulator; qpskDemod = comm.QPSKDemodulator; alamoutiEnc = comm.STBCEncoder( ... 'NumTransmitAntennas', Nt); alamoutiDec = comm.STBCCombiner( ... 'NumTransmitAntennas', Nt, ... 'NumReceiveAntennas', Nr); berCalcNC = comm.ErrorRate; |
A two-element resonant dipole array is used at both transmit (Tx) and receive (Rx) side. At Tx, the dipoles are spaced a half-wavelength apart. At Rx, the spacing is a tenth of a wavelength.
| txSpacing = 0.5; rxSpacing = 0.1; lambda = physconst('lightspeed')/fc; antElement = dipole( ... 'Length', lambda/2, ... 'Width', lambda/100); txArray = linearArray( ... 'Element', antElement,... 'NumElements', Nt,... 'ElementSpacing', txSpacing*lambda); rxArray = linearArray( ... 'Element', antElement,... 'NumElements', Nr,... 'ElementSpacing', rxSpacing*lambda); |
Then should change message to ['Hello world 0000','Hello world 0001','Hello world 0002','Hello world 0003','Hello world 0004','Hello world 0005','Hello world 0006'…]. The results are shown in these figures: ![[通信系统设计]Lab3 MIMO Programming_第7张图片](http://img.e-com-net.com/image/info8/43b8b4218ec3447792c24da73db94f17.jpg) ![[通信系统设计]Lab3 MIMO Programming_第8张图片](http://img.e-com-net.com/image/info8/bb3c443bfdf44f1d9233161b0e4cbd48.png)
Figure 2 the BER and Results of EBN0=0 and 10dB Then we can plot the relationship between BER and EBN0 curve. ![[通信系统设计]Lab3 MIMO Programming_第9张图片](http://img.e-com-net.com/image/info8/00ece1f1b7d840fb809a577437a2f8d0.jpg)
In addition, we can try to compare the capacity of SISO and MIMO by using MATLAB program. The key part of the MATLAB codes of this section are shown: In this section we choose 2*2 MIMO as an example to explore the differences of capacity of SISO and MIMO.
| r_M = 2; % Number of Receive Antennas of MIMO t_M = 2; % Number of Transmit Antennas of MIMO r_S = 1; % Number of Receive Antennas of SISO t_S = 1; % Number of Transmit Antennas of SISO N_M = min(r_M,t_M); N_S = min(r_S,t_S); H_M = zeros(r_M,t_M); % H-Matrix of Channel Coefficient of MIMO H_S = zeros(r_S,t_S); % H-Matrix of Channel Coefficient of SISO SNR_dB =[0:0.01:35]; % SNR in dB as a Vactor SNR = 10.^(SNR_dB/10); % Absolute Value of SNR |
| We can use Shannon Formula Capacity = log2(1+SNR) 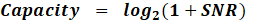 to compute the capacity. to compute the capacity. for k=1:N_M lamda(k) = V(k,k); Capacity_MIMO = Capacity_MIMO + log2(1+SNR*lamda(k)/t_M); % Capacity of MIMO end for k=1:N_S lamda_S(k) = V_S(k,k); Capacity_SISO = Capacity_SISO + log2(1+SNR*lamda_S(k/t_S)); % Capacity of SISO end |
The result was shown in this figure: ![[通信系统设计]Lab3 MIMO Programming_第10张图片](http://img.e-com-net.com/image/info8/9ee2efcb9a184725920e5322370462ce.jpg)
Figure 1 We can find that with SNR increasing, the differences between SISO and MIMO increases. And the capacity of MIMO is much larger than SISO which are same as we learnt in the theory class. |