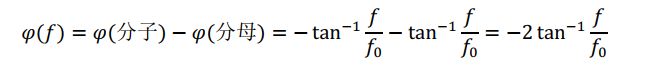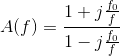2017年电赛题目-自适应滤波器

电赛题目解析之自适应滤波器

首先来看看题目： 2017全国大学生电子设计竞赛题目

这道题有很多发挥空间，本文将介绍三种电路：

1. 数字电位器移相模拟电路
2. 压控移相模拟电路
3. 数字方法

模拟电路方法

模拟电路实现的方法思想都大同小异，见下图。差别主要是可控移相器的实现方面。下面分别介绍各个部分的实现方式。

一、加法器电路

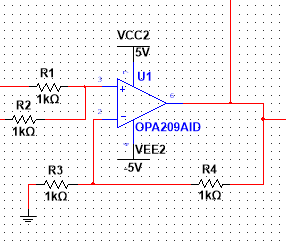
对于前级的加法器比较简单，这里贴出一种使用OPA209实现的常规做法：

输入端分别输入A信号和B信号就可以实现A+B，因为信号频率很低不涉及到阻抗匹配问题，所以这种接法没有问题。

二、移相器电路

1、数字电位器可控移相

移相器部分要求不对信号的幅值作用，只改变相位，所以首先想到的就是全通滤波器，题目要求移相范围为0-180°，二阶全通移相范围为0-360°，可以实现，但是调节比较复杂，这里采用一阶全通滤波器的方法。

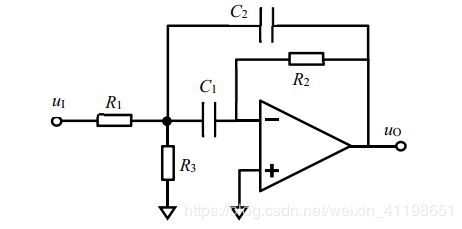
首先看一阶全通滤波器的电路拓扑：

先从滞后型全通开始说起，该电路的传递函数为

                                                                 

所以电压增益的模为：

                                                          

电压相移为：

                           

其中，

我们可以通过调节R的值来调节截止频率，从而调节移相角度。当时，移相角度为0°，当R=0时，移相角度为-180°。

同样可以得到超前型全通滤波器的电压相移为：

                               

当时，移相角度为180°，当R=0时，移相角度为0°。

从以上推导可以看出，一阶全通的移相范围已经达到了题目的要求范围，可是能实现吗？

答案是否定的，我们要实现0°的移相必须要交越0°而不是逼近0°，对于180°也是这样。需要对电路形式作出一定处理。

首先对于0°，可以通过添加预移相电路来实现，比如后级电路为0-180°超前一阶移相，前级为固定-30°移相（此处仅为例子，具体角度需要加以计算，后面会讲到），那么两级的移相角度为-30-150°，实现0°移相就比较稳妥。对于180°移相，我们可以采用两级一阶全通串联来实现，从而构成以下电路：

到现在为止，移相电路的整体思路已经完成，接下来进行一些元器件参数的具体计算：

前级固定移相角度为，.

后级可调移相角度为.

                                  

其中，是由数字电位器的分辨率决定的，一般数字电位器的分辨率为1024位，所以

根据题目条件，频率变化范围为10kHz-100kHz，所以得到以下约束条件：

最小移相角小于0°：                                                                                            

最大移相角大于180°：

 

最小移相角小于0°：

最大移相角大于180°：

通过求解以上的非线性不等式组可以得到及，再根据全通滤波器截止频率的公式，在RC乘积确定的情况下，根据手头现有的数字电位器阻值范围就可以确定R1,C1,R2,C2.R3,C3。（注意，只要RC乘积确定，同时改变R或者C，不会影响电路的至稳时间）。

至此，用数字电位器设计的移相器完成。

2、压控移相

数字电位器调节虽然可以达到要求，但毕竟不能连续调节，从上面的分析可以看出，限制条件主要是数字电位器的分辨率问题。而压控移相的步进取决于所用AD转换器的位数，带来了很大的发挥空间。

压控移相本质上也是一种滤波器，只不过可以通过改变控制电压来改变截止频率，从而改变移相角度。所以在这里还是要实现全通滤波器，压控滤波实现方法也有很多，先来看看原理。

                                         

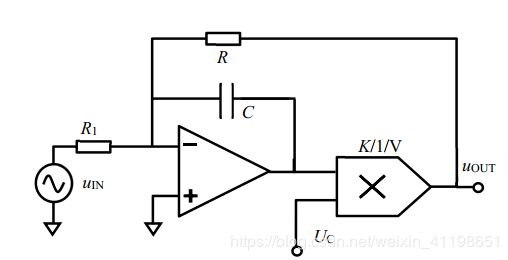
                                                                                        压控一阶低通滤波器

                       

可以看出，上图的压控滤波器只要改变乘法器的输入电压就可以改变截止频率，为了利用压控放大器VCA810等，我们对其作出一定修改：

                                        

                                                                                       修改后的压控一阶低通滤波器

将乘法器换成可控增益放大器后，就是将Uc=1，K=G，所以。

然后我们再来看看如何从一阶低通变成一阶全通滤波器，观察一阶低通和一阶全通滤波器的传函：

滞后型一阶全通滤波器传函：

超前型一阶全通滤波器传函：

反相输入一阶低通滤波器传函：

同相输入的一阶低通滤波器传函：

细心的小伙伴已经发现了，反相和同相输入一阶低通滤波器可以构成滞后型一阶全通：

（1）同相输入一阶低通滤波器：使得=2,则，即增益为2的低通滤波器减去原信号；

（2）反相输入一阶低通滤波器：使得=2,则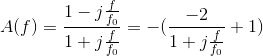，即增益为2的低通滤波器加上原信号后取反。

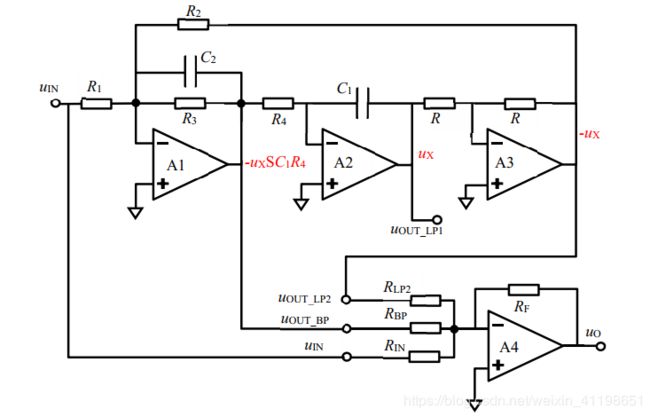
根据以上分析，用反相输入一阶低通滤波器及加法器可以设计以下电路，实现了0-180°全通移相：

将该电路代替数字电位器构成的全通滤波器，同样需要一级固定移相和两级可变来实现。

从该电路的设计过程中，可以进一步思考，高通滤波器来实现全通怎么设计？二阶的呢？是否可以一级实现0-360°移相？所以留给读者发挥的空间还很大，有想法的可以一起在评论区讨论。

我再来引申一下，其实压控增益的本质是增大了R2中流过的电流，因为R2的左侧因为虚短接地所以当施加G倍增益时，R2右侧的电压变为原来的G倍，用下图表示：

 

那么压控可以等效为，即构造了一个连续可调的压控电阻器，相比于数字电位器来说，如果采用VCA810（增益变化范围为-40dB-40dB）,电阻变化范围变成了，转化成数字电位器的，即我们构造的电阻器最大值和最小值之比为，这远大于常见数字电位器1024变化范围。

那么我们只要找到运放正输入端接地的滤波器电路我们就可以对它进行改造，在这里我想到如下几个：

                                                      

                                                                                    MFB窄带通滤波器

                                        

                                                                                                Biquad 滤波器

                                             

                                                                                        Fleischer-Tow 滤波器

 

  

三、减法器电路

减法器可以自己搭也可以用差动放大器，为了减少不必要的麻烦，这里采用AD629差动放大器来实现。

四、有效值检波电路

有效值检波电路采用的AD8436有效值检波芯片，需要仔细阅读器件手册获得比较好的动态性能，避免稳定时间较长。

还有一种思路就是把有效值检测交给FPGA或者单片机来处理。

五、快速有效的控制算法

上面四个部分已经实现了硬件部分设计，软件需要做的就是控制数字电位器或者是压控移相控制电压，不断对B路信号进行移相，使得经过减法器之后的信号有效值最小，即为滤除完全（两个非同频正弦信号叠加，不管相位如何，叠加后的信号有效值为叠加前信号有效值的均方根）。

我们回过头看看题目要求，“在1s内完成调节”，且最小频率差为10Hz，因为有效值检波芯片得到的有效值为真有效值，也就是叠加之后的信号有效值变化周期最长为0.1s，从有效值最小增加到有效值最大需要50ms，为了加速收敛过程，可以采用牛顿法迭代的思想：，为了方便计算，取滤波后信号有效值的平方。MATLAB模拟实现过程如下：

clc;
clear;
A1=0.5;  %A信号的有效值
A2=0.6;  %B信号的有效值
d0=pi/3; %B信号经过移相后的相角，随意调整
x=zeros(1,100);
x(1)=pi/2; %滤波器对B信号移相的角度初始值（对收敛次数重要）
y1_past=0;  
dx_past=0.1*pi;
for i=1:7  %迭代次数设置
    y1_current=2*A2^2*(1-cos(d0-x(i)));  %滤波后信号的有效值
    dx_next=-y1_current*dx_past/(y1_current-y1_past);%修正方程
    x_next=x(i)+dx_next;%修正相角
    y1_past=y1_current;
    dx_past=dx_next;
    x(i+1)=x_next;
end
y1_current/A2^2%将A1信号置零可以看滤波相对误差，可以对B信号实现1%一下衰减

从程序中可以得到，最小的迭代次数为7次，也就是350ms，时间充足。

数字方法实现

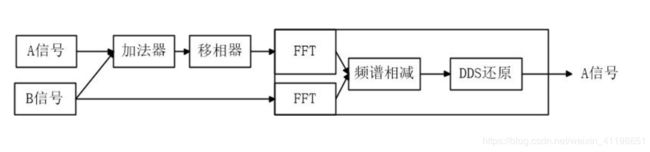
数字方法有LMS滤波等，这里采用一种比较新颖的方法，借助ZYNQ的FFT内核来实现。具体思路如下：

一、FFT算法怎么避免频谱泄漏

在实现过程中遇到的主要问题是FFT信号的频谱泄漏问题，即ZYNQ内核提供的最高采样点数N=65536，采样频率大于两倍信号频率即200kHz，那么频率分辨率最小为。问题的解决办法是通过添加窗函数来解决（补零法不可以哦）。我们采用了Hanning窗，相对于其他窗函数Hanning窗计算较为简单（其实每个窗函数都有自己的适用范围，Hanning窗经过尝试效果很好）

给出MATLAB实现代码（后续补上FPGA的程序）

close all; %先关闭所有图片
Adc=0; %直流分量幅度
A1=1.9;   %频率F1信号的幅度   A信号
A2=1.6; %频率F2信号的幅度     B信号
F1=100000; %信号1频率(Hz)    A信号频率
F2=99990; %信号2频率(Hz)    B信号频率
P1=-40; %信号1相位(度)   A信号经过移相器后相角
P2=90; %信号相位(度)    B信号经过移相器后相角

Fs=210000; %采样频率(Hz)
N=65536;   %采样点数
t=[0:1/Fs:N/Fs]; %采样时刻
%信号A+B
S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);
%信号B
SB=Adc+A2*cos(2*pi*F2*t);
%显示A+B经过移相后信号
plot(S);
title('A+B移相后信号');
%显示B原始信号
figure;
plot(SB);
%A+B移相后进行fft
F1=fft(S,N);
y1=abs(F1);
figure;
plot(y1(1:N)); %显示原始的FFT模值结果
%B原始信号进行FFt
F2=fft(SB,N);
y2=abs(F2);
figure;
plot(y2(1:N));

%将A+B移相后的fft结果与原始Bfft结果相减，得到A的fft
ya=y1-y2;
figure;
plot(ya);
%对A的频谱进行处理得到A的有效值
[Y1, k]=max(ya(2:N/2));
k=k+1;   %得到A频率所在位置
z1=F1(k)-(F1(k-1)+F1(k+1))/2;  %利用A+B的fftA的相关部分
z2=F1(k+1)-(F1(k)+F1(k+2))/2;
ka=abs(z1)/abs(z2);
r=(2-ka)/(1+ka);
fo=(k-1+r)*Fs/N  %得到A信号的频率
ao=2*pi*r*(1-r*r)*(abs(z1))/(N*sin(r*pi))  %得到A信号的幅值

二、如何设计DDS波形发生器

可以参考下面的例程：

基于FPGA的SPI通信控制DDS信号发生器

基于FPGA的DDS信号发生器