《剑指offer》算法题二刷整理
二刷把这75道题的思路重新整理(拒绝使用暴力法),同时按自己的编码风格再写了一遍。
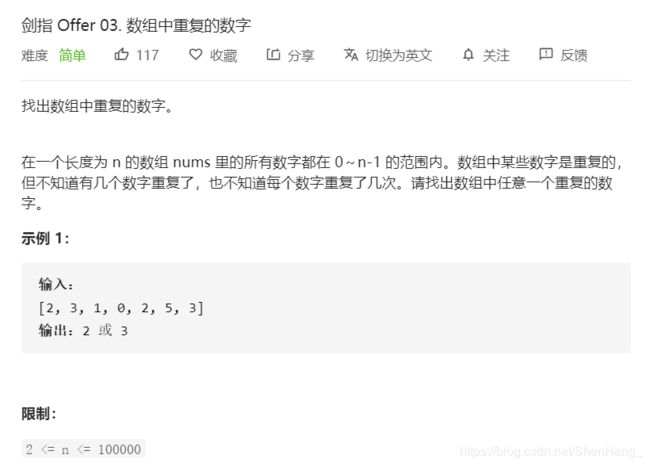
法1:set
空间复杂度O(n)
每一个数字在哈希表中查找的时间为O(1)
所以算法总的时间复杂度为O(n)
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
set<int>myset;
for(int elem:nums)
{
if(myset.find(elem)!=myset.end())
{
return elem;
}
else
{
myset.insert(elem);
}
}
return -1;
}
};
法2:数组中交换元素(很经典的方法)
空间复杂度O(1)
算法总的时间复杂度为O(n)
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
for(int i=0;i<nums.size();i++)
{
while(i!=nums[i])
{
if(nums[nums[i]]==nums[i])
return nums[i];
swap(nums[i],nums[nums[i]]);
}
}
return -1;
}
};
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
//从右上开始
if(matrix.empty()|| matrix[0].empty())return false;
int rows=matrix.size();
int cols=matrix[0].size();
int row=0,col=cols-1;
while(row<rows&&col>=0)
{
if(matrix[row][col]==target)
{
return true;
}
else if(matrix[row][col]>target)
{
col--;
}
else
{
row++;
}
}
return false;
}
};
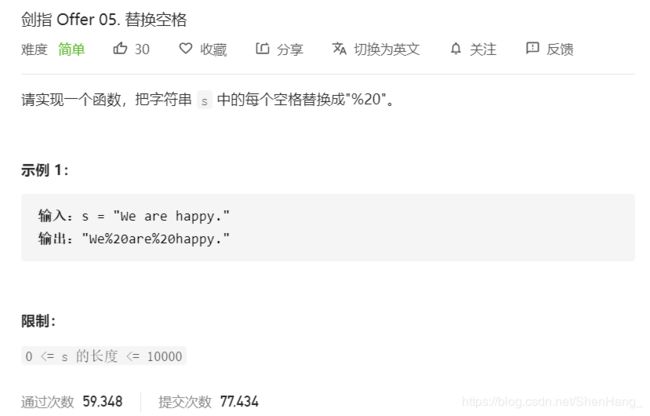
class Solution {
public:
string replaceSpace(string s) {
//双指针
//先扩容
//' '被替换为"%20",所以相当于1个空格需要多扩容2个字符
int old_len=s.size();
for(int i=0;i<old_len;i++)
{
if(s[i]==' ')
s+="00";
}
int p1=old_len-1,p2=s.size()-1;//双指针,从后往前
while(p1!=p2)
{
if(s[p1]!=' ')
{
s[p2--]=s[p1--];
}
else
{
p1--;
s[p2--]='0';
s[p2--]='2';
s[p2--]='%';
}
}
//追上了说明已经替换完所有的空格了
return s;
}
};
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
//DFS
if(head==NULL)return {};
vector<int>res;
DFS(head,res);
return res;
}
void DFS(ListNode*head,vector<int>&res)
{
if(head!=NULL)
{
DFS(head->next,res);
res.push_back(head->val);
}
}
};
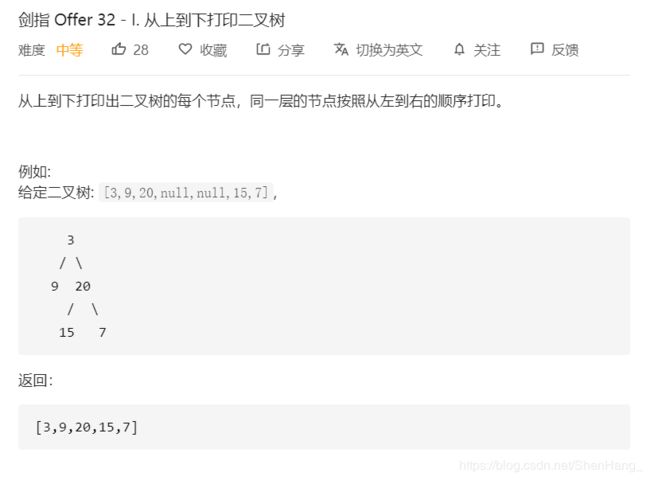
![]()
老题目了,经典DFS
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size()==0||inorder.size()==0)
return NULL;
return DFS(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1);
}
TreeNode*DFS(vector<int>& preorder,int pre_start,int pre_end,vector<int>& inorder,int in_start,int in_end)
{
if(pre_start>pre_end||in_start>in_end)
return NULL;
TreeNode*root=new TreeNode(preorder[pre_start]);
//在中序序列中找到根结点
int root_index;
for(int i=in_start;i<=in_end;i++)
{
if(inorder[i]==root->val)
{
root_index=i;
break;
}
}
int left_length=(root_index-1)-in_start+1;
int right_length=in_end-(root_index+1)+1;
root->left=DFS(preorder,pre_start+1,pre_start+left_length,inorder,in_start,root_index-1);
root->right=DFS(preorder,pre_end-right_length+1,pre_end,inorder,root_index+1,in_end);
return root;
}
};
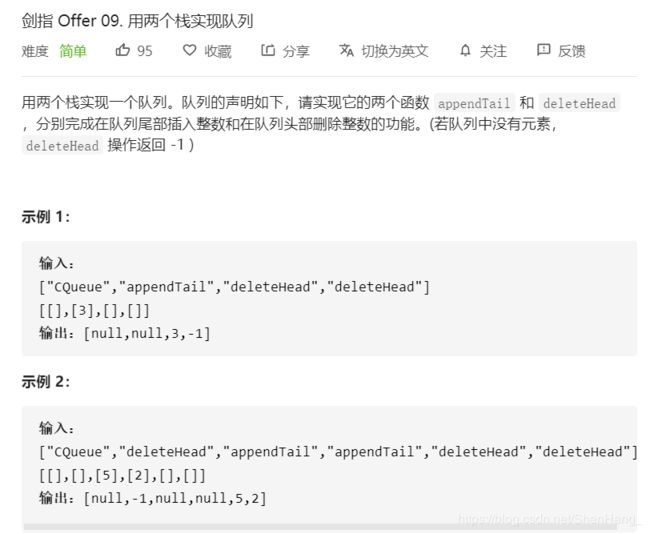
class CQueue {
public:
stack<int>s1,s2;
CQueue() {
}
void appendTail(int value) {//入队
s1.push(value);
}
int deleteHead() {//出队列
if(s2.empty()&&s1.empty())
{
return -1;
}
if(!s2.empty())
{
int temp=s2.top();
s2.pop();
return temp;
}
//当s2为空时
while(!s1.empty())
{
s2.push(s1.top());
s1.pop();
}
int temp=s2.top();
s2.pop();
return temp;
}
};
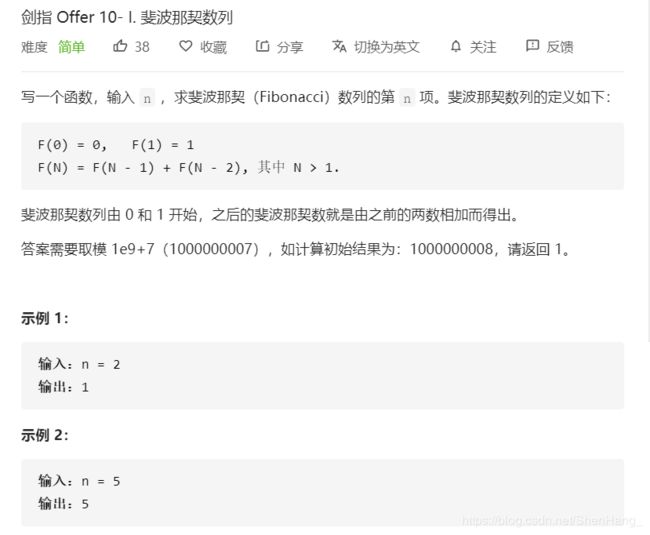
class Solution {
public:
int fib(int n) {
if(n<=1)return n;
vector<int>dp(n+1,0);
dp[0]=0;
dp[1]=1;
for(int i=2;i<=n;i++)
dp[i]=(dp[i-1]+dp[i-2])%1000000007;
return dp[n];
}
};
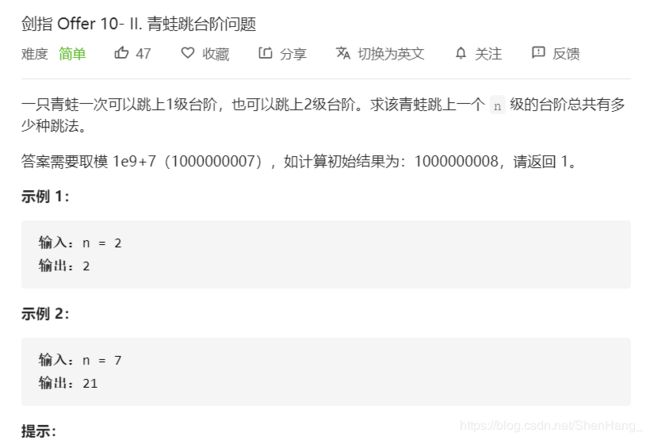
class Solution {
public:
int numWays(int n) {
//dp[i]表示能到达第i阶的方法总数
//dp[i]=dp[i-1]+dp[i-2]
if(n==0)return 1;
if (n <= 2)return n;
vector<int>dp(n + 1, 0);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
dp[i]=dp[i] % 1000000007;
}
return dp[n];
}
};
class Solution {
public:
int minArray(vector<int>& numbers) {
//二分法
if(numbers.size()==0)
return -1;
int low=0,high=numbers.size()-1;
while(low<high)
{
int mid=(low+high)/2;
if(numbers[mid]>numbers[high])//此时中间元素一定在前面的递增序列
{
//显然,分割点在右边
low=mid+1;
}
else if(numbers[mid]<numbers[high])//此时中间元素一定在后面的递增序列
{
//显然,分割点在左边(mid本身也有可能是分割点)
high=mid;
}
else//此时中间元素在前段还是后段不确定!!!(有这样的特例)
{
//去重
high--;
}
}
return numbers[low];
}
};
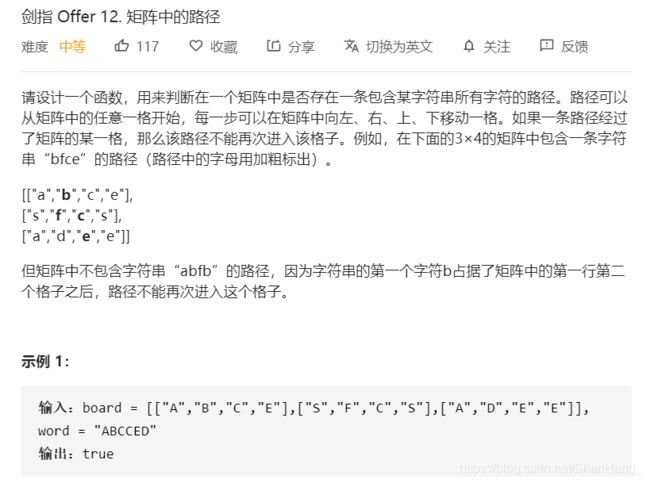
class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
//回溯
if (board.empty() || board[0].empty())return word.empty();
vector<vector<bool>>visited(board.size(), vector<bool>(board[0].size(), false));
for (int i = 0; i < board.size(); i++)
for (int j = 0; j < board[0].size(); j++)
{
if (DFS(board, word, visited, i, j, 0))
return true;
}
return false;
}
bool DFS(vector<vector<char>>& board, string&word, vector<vector<bool>>& visited, int cur_x, int cur_y, int count)
{
if (word.size() == count)
return true;
if (cur_x >= 0 && cur_x <= board.size() - 1 && cur_y >= 0 && cur_y <= board[0].size() - 1 && !visited[cur_x][cur_y] && word[count] == board[cur_x][cur_y])
{
visited[cur_x][cur_y] = true;
if (DFS(board, word, visited, cur_x + 1, cur_y, count + 1)
| DFS(board, word, visited, cur_x - 1, cur_y, count + 1)
| DFS(board, word, visited, cur_x, cur_y + 1, count + 1)
| DFS(board, word, visited, cur_x, cur_y - 1, count + 1))
return true;
visited[cur_x][cur_y] = false;//回溯
}
return false;
}
};
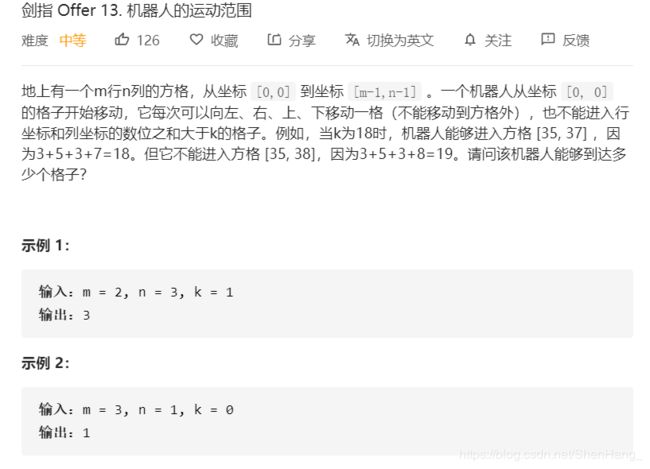
class Solution {
public:
int movingCount(int m, int n, int k) {
int count = 0;
if (k < 0 || m <= 0 || n <= 0)
return count;
if(k==0)return 1;//只有原点符合
bool*visited=new bool[m*n];
memset(visited,0,m*n);
int start_x = 0, start_y = 0;
//以上均为初始化
count=DFS(start_x,start_y,m,n,k,visited);
delete[]visited;
return count;
}
int DFS(int cur_x,int cur_y,int m,int n,int k,bool*visited)
{
int count=0;
if (cur_x >= 0 && cur_x < m&&cur_y >= 0 && cur_y < n && !visited[cur_x*n + cur_y] && getcurrentSum(cur_x) + getcurrentSum(cur_y) <= k)
{
visited[cur_x*n + cur_y]=true;//表示已经遍历过
//接下来开启新的子递归
count+=1+DFS(cur_x+1,cur_y,m,n,k,visited)
+DFS(cur_x-1,cur_y,m,n,k,visited)
+DFS(cur_x,cur_y+1,m,n,k,visited)
+DFS(cur_x,cur_y-1,m,n,k,visited);
}
return count;
}
int getcurrentSum(int num)
{
int sum = 0;
while (num)
{
sum += num % 10;
num /= 10;
}
return sum;
}
};
class Solution {
public:
int cuttingRope(int n) {
//dp[i]=max(dp[i]*dp[n-i])
if(n<=1)return 0;//至少要剪1刀
if(n==2)return 1;//至少要剪1刀
if(n==3)return 2;//至少要剪1刀
vector<int>dp(n+1,0);
dp[0]=0;
dp[1]=1;
dp[2]=2;
dp[3]=3;
for(int i=4;i<=n;i++)
for(int j=1;j<=i/2;j++)
{
dp[i]=max(dp[i],dp[j]*dp[i-j]);
}
return dp[n];
}
};
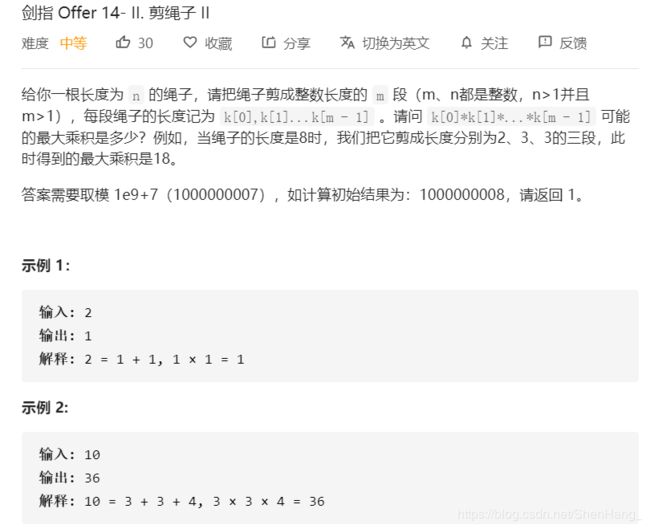
class Solution {
public:
int cuttingRope(int n) {
//这一题已经不能用动态规划了,取余之后max函数就不能用来比大小了。
//这题就是题目强制要我们使用贪心算法
if(n<=1)return 0;
if(n==2)return 1;//至少剪1刀
if(n==3)return 2;
int time_of_3=n/3;//尽可能剪成长度为3的section,最好的情况就是能整除
//当对3取余的余数为1时,最后的4不能简单处理为3*1,而是应该剪成2*2
if(n-time_of_3*3==1)
{
time_of_3--;
}
int time_of_2=(n-time_of_3*3)/2;
long int res=1;
while(time_of_3--)
{
res*=3;
res=res%1000000007;
}
while(time_of_2--)
{
res*=2;
res=res%1000000007;
}
return res;
}
};
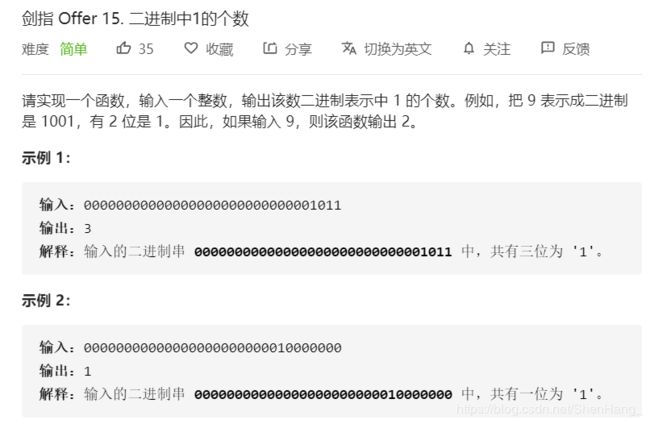
class Solution {
public:
int hammingWeight(uint32_t n) {
//无符号数右移高位补0,不会出问题
int count=0;
while(n)
{
if(n&1)
count++;
n>>=1;
}
return count;
}
};
class Solution {
public:
int hammingWeight(int n) {
int count=0;
while(n)
{
count++;
n=n&(n-1);
}
return count;
}
};
class Solution {
public:
double myPow(double x, int n) {
//考察快速幂乘算法
if (x == 0)return -1;
if (n == 0)return 1;
if (n < 0)
x = 1. / x;
bool flag = 1;//1表示结果为正,0表示结果为负
if (x < 0)
{
x = -x;
if (n % 2 != 0)
{
flag = 0;
}
}
double ans = 1;
double base = x;
while (n)
{
if (n % 2)
{
ans *= base;
}
base *= base;
n /= 2;
}
if (flag == 0)
ans = -ans;
return ans;
}
};
class Solution
{
public:
vector<int> res;
vector<int> printNumbers(int n) {
if (n <= 0) return res;
string number(n, '0');
for (int i = 0; i <= 9; i++)
//从高位到低位进行全排列
{
number[0] = '0'+i;//首字符赋初值
DFS(number, n, 1);//设置下一位
}
return res;
}
//对数字全排列
void DFS(string& number, int length, int index) {
if (index == length) {//递归结束
saveNumber(number);//存储结果
return;
}
else
{
for (int i = 0; i <= 9; i++)
{
number[index] = '0' + i;
DFS(number, length, index + 1);
}
}
}
//存储结果
//注意处理0开头的字符串
void saveNumber(string&number) {
bool isBegin0 = true;
string temp = "";
for (string::iterator it=number.begin();it != number.end();++it)
{
if (isBegin0 && *it != '0') isBegin0 = false;
if (!isBegin0)
{
temp += *it;
}
}
//从高位到低位全排列,要注意字符串元素全为0时,temp为空,不能执行stoi
if (!temp.empty())
{
res.push_back(stoi(temp));//stoi函数很方便!
}
}
};
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head==NULL)return NULL;
if(head->val==val)
{
return head->next;
}
ListNode*cur=head;
ListNode*prev=NULL;
while(cur->val!=val)
{
prev=cur;
cur=cur->next;
}
prev->next=cur->next;
return head;
}
};
class Solution {
public:
bool isMatch(string s, string p) {
//如果正则串p为空且字符串s也为空则匹配成功,如果正则串p为空但是s不为空则说明匹配失败
if (p.empty())return s.empty();
//判断s和p的首字符是否匹配,注意要先判断s不为空(因为能执行下面这句话本身就说明p不为空了)
bool headMatched = !s.empty() && (s[0] == p[0] || p[0] == '.');
if (p.length() >= 2 && p[1] == '*')
{
//如果p的第一个元素的下一个元素是*,则分别对两种情况进行判断
return isMatch(s, p.substr(2)) || (headMatched&&isMatch(s.substr(1), p));
}
else if (headMatched)
{
//否则,如果s和p的首字符相等,则s和p同时后移一位继续判断
return isMatch(s.substr(1), p.substr(1));
}
else
return false;
}
};
class Solution {
public:
//1.定义两个分别指向数组第一个数字和最后一个数字的指针;
//2.前一指针右移,后一指针左移,直到后一指针移动到前一指针的前面;
//3.当前一指针指向的数字为偶数,后一指针指向的数字为奇数时,交换这两个数字。
vector<int> exchange(vector<int>& nums) {
int i=0,j=nums.size()-1;
while(i<=j)
{
if(isEven(nums[i]))
{
if(!isEven(nums[j]))
swap(nums[i++],nums[j--]);
else
{
j--;
}
}
else
{
i++;
}
}
return nums;
}
bool isEven(int n)//偶数
{
if((n&0x1)==0)//注意优先级!!
return true;
return false;
}
};
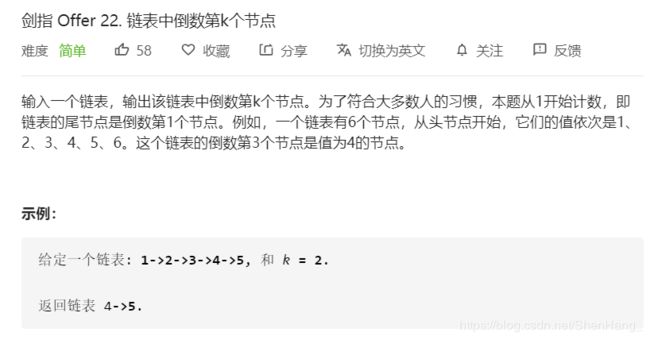
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
ListNode*dummy=new ListNode(-1);
dummy->next=head;
ListNode*p1=dummy,*p2=dummy;
while(k--)
{
p1=p1->next;
}
while(p1!=NULL)
{
p1=p1->next;
p2=p2->next;
}
return p2;
}
};
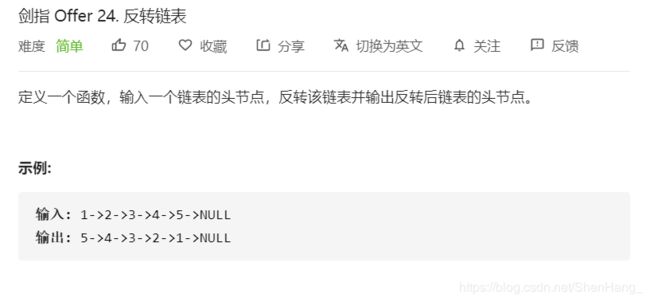
class Solution {
public:
ListNode* reverseList(ListNode* head) {
//迭代
ListNode*cur=head;
ListNode*prev=NULL;
while(cur!=NULL)
{
ListNode*temp=cur->next;
cur->next=prev;
prev=cur;
cur=temp;
}
return prev;
}
};
class Solution {
public:
ListNode* reverseList(ListNode* head) {
//递归
if(head==NULL||head->next==NULL)return head;
ListNode*new_head=reverseList(head->next);//完成子链表的反转 cur-->node<--node<--...node<--new_head
head->next->next=head;
head->next=NULL;
return new_head;
}
};
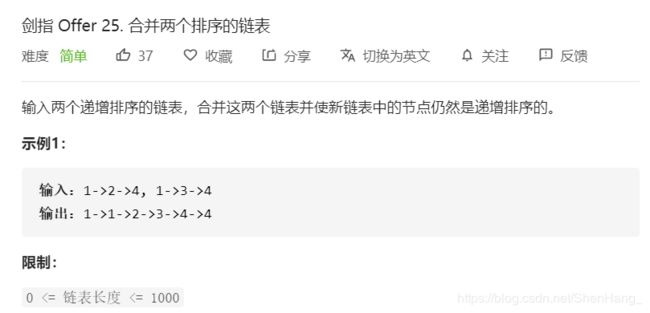
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode*dummy=new ListNode(-1);
ListNode*temp=dummy,*t1=l1,*t2=l2;
while(t1!=NULL||t2!=NULL)
{
if(t1==NULL)
{
temp->next=t2;
return dummy->next;
}
else
if(t2==NULL)
{
temp->next=t1;
return dummy->next;
}
else
{
if(t1->val<=t2->val)
{
temp->next=t1;
temp=temp->next;
t1=t1->next;
temp->next=NULL;
}
else
{
temp->next=t2;
temp=temp->next;
t2=t2->next;
temp->next=NULL;
}
}
}
return dummy->next;
}
};
递归
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1==NULL)return l2;
if(l2==NULL)return l1;
if(l1->val<=l2->val)
{
l1->next=mergeTwoLists(l1->next,l2);
return l1;
}
else
{
l2->next=mergeTwoLists(l1,l2->next);
return l2;
}
}
};
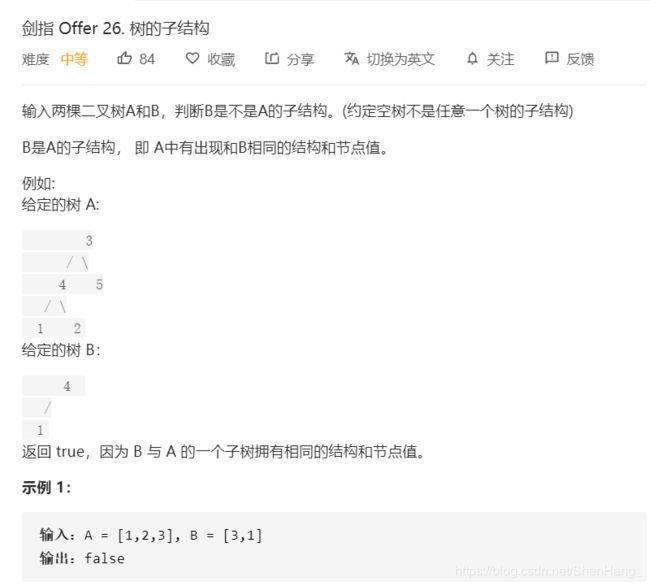
class Solution {
//双递归!
public:
bool isSubStructure(TreeNode* A, TreeNode* B)//遍历A树的每一个结点,每个结点都当一次根结点
{
if (A==NULL||B==NULL) return false;
return DFS(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
bool DFS(TreeNode* A, TreeNode* B)//判断B是否为A的子结构
{
if (B==NULL) return true;
if (A==NULL) return false;
return A->val == B->val && DFS(A->left, B->left) && DFS(A->right, B->right);
}
};
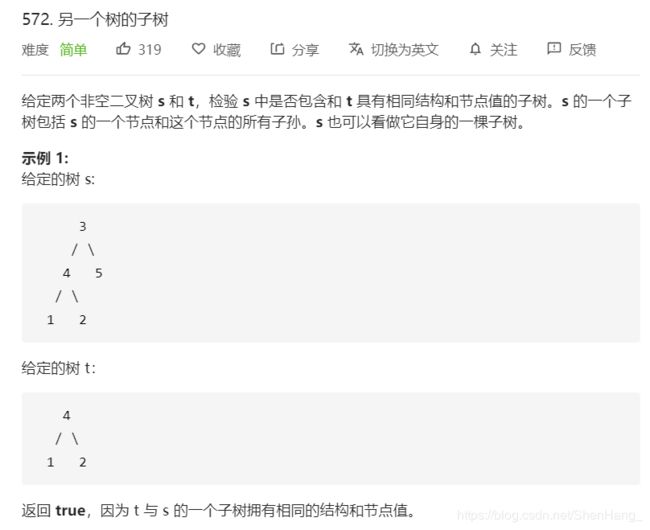
class Solution {
public:
//双递归
bool isSubtree(TreeNode* s, TreeNode* t)//遍历s的所有结点
{
if (s == NULL && t == NULL) return true;
if(s==NULL||t==NULL)return false;
return DFS(s,t) || isSubtree(s->left, t)|| isSubtree(s->right, t);
}
bool DFS(TreeNode* s, TreeNode* t) //判断树t是否是树s的子树
{
if (s == NULL && t == NULL) return true;
if (s != NULL && t != NULL)
return s->val==t->val && DFS(s->left, t->left)&& DFS(s->right, t->right);
return false;
}
};
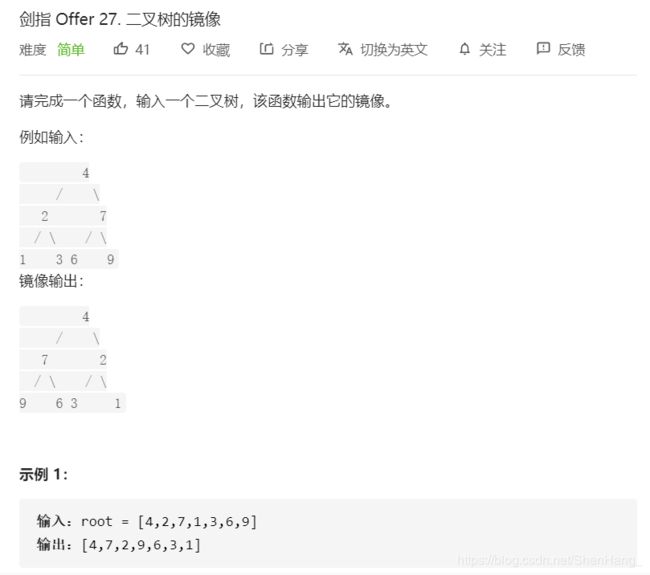
class Solution {
public:
//递归交换每个结点的左右子结点
TreeNode* mirrorTree(TreeNode* root) {
if(root==NULL)return NULL;
TreeNode*temp=root->left;
root->left=root->right;
root->right=temp;
mirrorTree(root->left);
mirrorTree(root->right);
return root;
}
};
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root==NULL)
return true;
return DFS(root->left,root->right);
}
bool DFS(TreeNode*t1,TreeNode*t2)
{
if(t1==NULL&&t2==NULL)return true;
if(t1!=NULL&&t2!=NULL)
{
if(t1->val==t2->val)
{
return DFS(t1->left,t2->right)&&DFS(t1->right,t2->left);
}
}
return false;
}
};
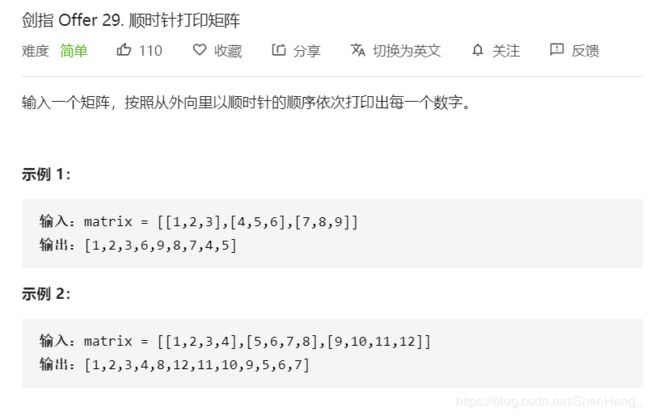
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if(matrix.size()==0)
return {};
int rows=matrix.size();
int cols=matrix[0].size();
vector<int>res;
int left=0,right=cols-1,top=0,bottom=rows-1;
while(left<=right&&top<=bottom)
{
//从左到右
for(int i=left;i<=right;i++)
{
res.push_back(matrix[top][i]);
}
//从上到下
for(int i=top+1;i<=bottom;i++)
{
res.push_back(matrix[i][right]);
}
//从右往左(有条件,防止出现行向量的情况)
if(top!=bottom)
{
for(int i=right-1;i>=top;i--)
{
res.push_back(matrix[bottom][i]);
}
}
//从下往上(有条件,防止出现列向量的情况)
if(left!=right)
{
for(int i=bottom-1;i>=top+1;i--)
{
res.push_back(matrix[i][left]);
}
}
//更新,为下一轮准备
left++;
right--;
top++;
bottom--;
}
return res;
}
};
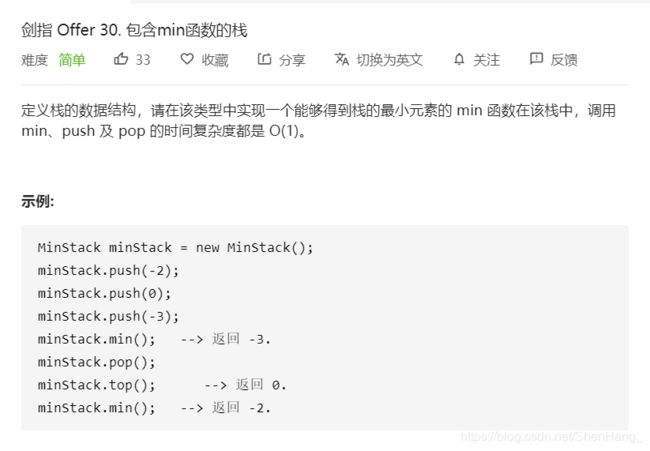
class MinStack {
public:
/** initialize your data structure here. */
stack<int>s1,s2;//s1是数据栈,s2是辅助栈
int min_value=INT_MAX;;
MinStack() {
}
void push(int x) {
if(x<min_value)
{
min_value=x;
}
s1.push(x);
s2.push(min_value);
}
void pop() {
if(!s1.empty())
{
s1.pop();
s2.pop();
}
if(s1.empty())
{
min_value=INT_MAX;
}
else
{
min_value=s2.top();
}
}
int top() {
return s1.top();
}
int min() {
return s2.top();
}
};
//找规律:如果下一个要弹出的数字刚好是栈顶数字,那么直接弹出;如果下一个要弹出的数字不在栈顶,则把压栈序列中还没有入栈的数字压入辅助栈,直到把需要的数字压入为止;如果所有数字都压入后还没有找到需要的数字,那么return false;
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> s;
int j = 0;//用来标记poped数组出栈的元素
for(int i = 0; i < pushed.size(); i ++) {
s.push(pushed[i]);//入栈pushed数组元素
//如果入栈元素为要出栈的元素,进行出栈,直到不需要出栈为止
while(!s.empty() && s.top() == popped[j]) {
s.pop();
j++;
}
}
return s.empty();
}
};
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
if(root==NULL)return {};
vector<int>res;
queue<TreeNode*>my_queue;
my_queue.push(root);
while(!my_queue.empty())
{
int size=my_queue.size();
for(int i=0;i<size;i++)
{
res.push_back(my_queue.front()->val);
if(my_queue.front()->left)
my_queue.push(my_queue.front()->left);
if(my_queue.front()->right)
my_queue.push(my_queue.front()->right);
my_queue.pop();
}
}
return res;
}
};
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(root==NULL)return {};
vector<vector<int>>res;
queue<TreeNode*>my_queue;
my_queue.push(root);
while(!my_queue.empty())
{
vector<int>temp;
int size=my_queue.size();
for(int i=0;i<size;i++)
{
temp.push_back(my_queue.front()->val);
if(my_queue.front()->left)
my_queue.push(my_queue.front()->left);
if(my_queue.front()->right)
my_queue.push(my_queue.front()->right);
my_queue.pop();
}
res.push_back(temp);
}
return res;
}
};
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(root==NULL)return {};
deque<TreeNode*>my_deque;
my_deque.push_back(root);
vector<vector<int>>res;
bool flag=0;//0表示从左往右,1表示从右往左
while(!my_deque.empty())
{
vector<int>temp;
int size=my_deque.size();
if(flag==1)
{
for(int i=0;i<size;i++)
{
temp.push_back(my_deque.back()->val);
if(my_deque.back()->right)//前插时先插右后插左
my_deque.push_front(my_deque.back()->right);
if(my_deque.back()->left)
my_deque.push_front(my_deque.back()->left);
my_deque.pop_back();
}
}
else
{
for(int i=0;i<size;i++)
{
temp.push_back(my_deque.front()->val);
if(my_deque.front()->left)//后插时先插左后插右
my_deque.push_back(my_deque.front()->left);
if(my_deque.front()->right)
my_deque.push_back(my_deque.front()->right);
my_deque.pop_front();
}
}
res.push_back(temp);
flag=!flag;
}
return res;
}
};
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
if(postorder.size()==0)return true;
return DFS(postorder,0,postorder.size()-1);
}
bool DFS(vector<int>& postorder,int start,int end)
{
if(start>=end)
return true;
int root=postorder[end];
int index=-1;//先找左子树序列和右子树序列的分界点index
for(int i=start;i<=end-1;i++)
{
if(postorder[i]>root)
{
index=i;
break;
}
}
if(index==-1)return DFS(postorder,start,end-1);
//判断右子树序列中的元素是否都比根结点大
for(int i=index;i<=end-1;i++)
{
if(postorder[i]<=root)
return false;
}
return DFS(postorder,start,index-1)&&DFS(postorder,index,end-1);
}
};
class Solution {
private:
vector<vector<int>>res;
vector<int>cur;
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
if(root==NULL)return {};
DFS(root,sum);
return res;
}
void DFS(TreeNode*root,int sum)
{
if(root==NULL)return;
cur.push_back(root->val);
if(root->left==NULL&&root->right==NULL)
{
if(sum-root->val==0)
{
res.push_back(cur);
//cur.pop_back();
//return;
}
}
DFS(root->left,sum-root->val);
DFS(root->right,sum-root->val);
cur.pop_back();
}
};
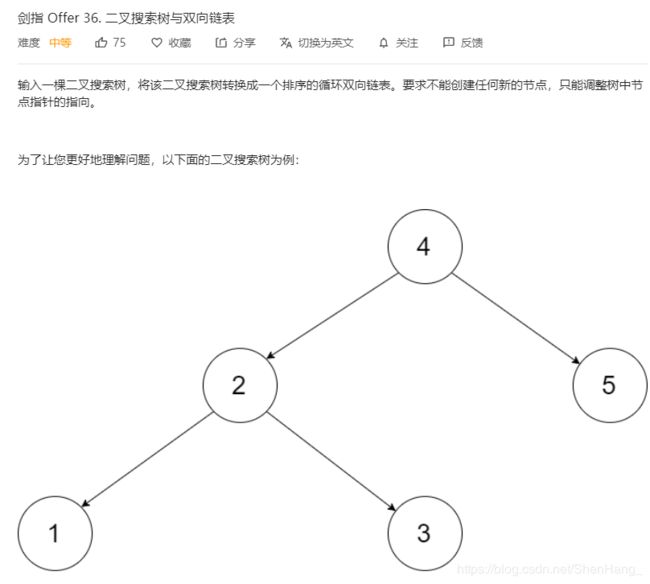
重点题,很棒的DFS!
要在函数中修改pre和head,所以必须传入二重指针或者一重指针的引用,这点不用强调了,很简单。
class Solution {
public:
//最简单的方法当然是先把中序遍历的结点存到vector中,然后再处理即可。
//下面看一看用DFS的方法,不使用额外空间
Node* treeToDoublyList(Node* root) {
if(root==NULL)return NULL;
Node*head=NULL,*prev=NULL;
DFS(root,head,prev);
//最后完成头尾连接
head->left=prev;
prev->right=head;
return head;
}
void DFS(Node*root,Node*&head,Node*&prev)
{
if(root==NULL)return;
DFS(root->left,head,prev);//中序遍历
if(head==NULL)
{
head=root;//找到中序遍历的首结点,也就是链表的头结点
}
//开始拼接
if(prev!=NULL)
prev->right=root;
root->left=prev;
prev=root;
DFS(root->right,head,prev);
}
};
class Solution {
public:
vector<string> permutation(string s) {
vector<string>res;
string temp;
vector<bool>used(s.size(), false);
sort(s.begin(), s.end());
DFS(res, temp, used, s, 0);
return res;
}
void DFS(vector<string>& res, string& temp, vector<bool>&used, string& s, int start)
{
if (start == s.size())
{
res.push_back(temp);
return;
}
for (int i = 0; i < s.size(); i++)
{
if (used[i] == true)
continue;
if (i >= 1 && used[i - 1] == false && s[i] == s[i - 1])
continue;
used[i] = true;
temp.append(1,s[i]);
DFS(res, temp, used, s, start + 1);
temp.pop_back();
used[i] = false;
}
}
};
class Solution {
public:
//法1:找中位数即可
int majorityElement(vector<int>& nums) {
int middle=nums.size()/2;
int pivot=partition(nums,0,nums.size()-1);
while(pivot!=middle)
{
if(pivot>middle)//middle在左边
{
pivot=partition(nums,0,pivot-1);
}
else//middle在右边
{
pivot=partition(nums,pivot+1,nums.size()-1);
}
}
return nums[pivot];
}
int partition(vector<int>& nums,int low,int high)
{
while(low<high)
{
while(low<high&&nums[low]<=nums[high])high--;//low为枢轴
swap(nums[low],nums[high]);
while(low<high&&nums[low]<=nums[high])low++;//high为枢轴
swap(nums[low],nums[high]);
}
return low;
}
};
法2:摩尔投票法
很简单的方法!
class Solution {
public:
//法2:摩尔投票算法
int majorityElement(vector<int>& nums) {
int votes=1,x=nums[0];
for(int i=1;i<nums.size();i++)
{
if(votes==0)
{
x=nums[i];
votes=1;
}
else if(x==nums[i])
{
votes++;
}
else
{
votes--;
}
}
return x;
}
};
class Solution {
public:
int maxSubArray(vector<int>& nums) {
if (nums.empty())
return 0;
int maxsum = nums[0];//初始化
int currsum = nums[0];//初始化
for (int i = 1; i < nums.size(); i++)
{
if (currsum <= 0)//如果当前位置之前“累加子数组”的和小于等于0,则抛弃当前位置之前的“累加子数组”的和,从当前元素开始重新累加
currsum = nums[i];
else
currsum += nums[i];
if (currsum > maxsum)
maxsum = currsum;
}
return maxsum;
}
};

Top K问题,最好的方法是用堆排序,时间复杂度O(nlogk)
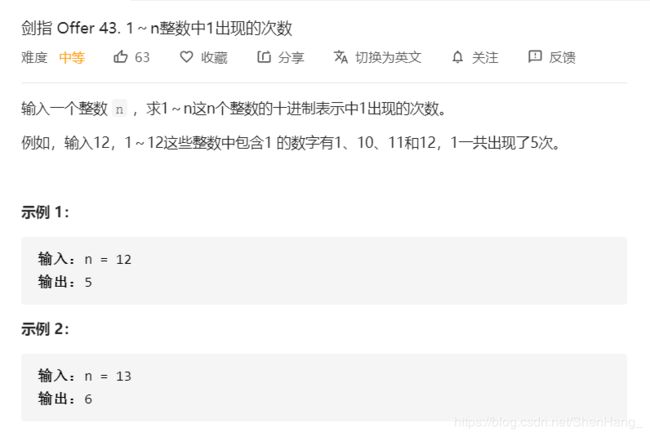
这题是找规律的题目,我不想在这里浪费时间,只写出通用的解法(leetcode不能AC):
class Solution {
public:
int countDigitOne(int n) {
int count=0;
for(int i=0;i<=n;i++)
count+=number_of_1(i);
return count;
}
int number_of_1(int n)
{
int count=0;
while(n)
{
if(n%10==1)
count++;
n/=10;
}
return count;
}
};
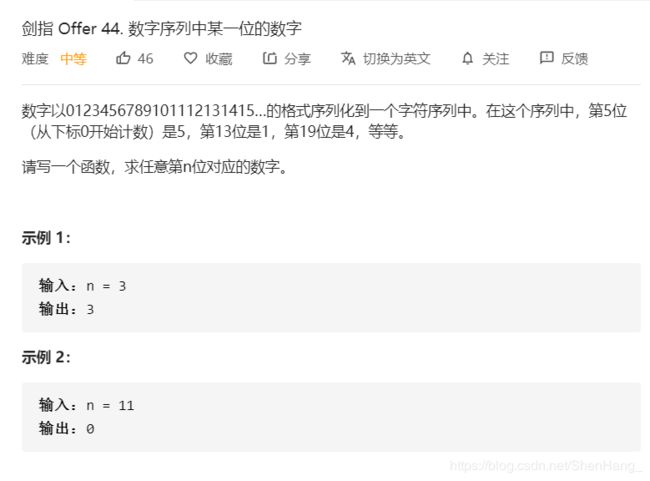
分析规律:
首先,题目要求下标从0开始,为了方便,我们先定义下标从1开始。
如求序列的第1001位是什么?(下标从0开始)
首先把题目换一种说法,求序列的第1002位是什么?(下标从1开始)
1位数序列前10位是0 ~ 9,显然1002在10后面,所以问题变为从10 ~ 开始,找第992位。
2位数序列10 ~ 99共180位,显然,992在180后面,所以问题变为从100 ~ 开始,找第812位。
3位数序列100 ~ 999共2700位,显然,812在2700中,且812=270*3+2。因为100对应下标为1,所以下标270对应的数字为369(100~269共有270个数),所以最后的结果就是370的中间那一位,也就是7!
class Solution {
public:
int findNthDigit(int x) {
long long n = (long long)x + 1;//转换题意,下标从1开始
//先判断第n位是在一个几位数中
int count = 1;
while (1)
{
if (n > (long long)count*count_of_int(count))
{
n -= count*count_of_int(count);
count++;
}
else
{
break;
}
}
int int_part = n / count;
int mod_part = n%count;
int begin = begin_number(count);
int target = begin + int_part;
if (mod_part == 0)
{
return (target - 1) % 10;//如果余数为0的情况
}
else
{
//找到target的从左往右数第mod_part位,也就是从右往左数第count-mod_part+1位
for (int i = 1; i <= count - mod_part; i++)
{
target /= 10;
}
return target % 10;
}
}
int count_of_int(int m)//返回的是m位数共有几个数,比如一位数共有9-0+1即10个,两位数共有99-10+1即90个,三位数共有999-100+1即900个
{
if (m == 1)
return 10;
int count = (int)pow(10, m - 1);
return count * 9;
}
int begin_number(int m)//比如一位数从0开始,两位数从10开始,三位数从100开始
{
if (m == 1)return 0;
return (int)pow(10, m - 1);
}
};
class Solution {
public:
string minNumber(vector<int>& nums) {
vector<string> v;
for(int elem:nums)
v.push_back(to_string(elem));
sort(v.begin(),v.end(),[](string&s1,string&s2)->bool{return s1+s2<s2+s1;});
string res;
for(string elem:v)
res+=elem;
return res;
}
};
法2:使用functor
class functor
{
public:
bool operator()(string&s1,string&s2)
{
return s1+s2<s2+s1;
}
};
class Solution {
public:
string minNumber(vector<int>& nums) {
vector<string> v;
for(int elem:nums)
v.push_back(to_string(elem));
sort(v.begin(),v.end(),functor());
string res;
for(string elem:v)
res+=elem;
return res;
}
};
class Solution {
public:
int translateNum(int num) {
string s = to_string(num);
if(s.size()==1)return 1;
vector<int>dp(s.size(), 0);
//初始化
dp[0] = 1;
string temp;
temp += s[0];
temp += s[1];
dp[1] = stoi(temp) >= 10 && stoi(temp) <= 25 ? 2 : 1;
for (int i = 2; i <= s.size() - 1; i++)
{
string temp;
temp += s[i-1];
temp += s[i];
if (stoi(temp) >= 10 && stoi(temp) <= 25)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
else
{
dp[i] = dp[i - 1];
}
}
return dp[s.size()-1];
}
};
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
//dp[i][j]表示从(0,0)到(i,j)能拿到的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
int m=grid.size(),n=grid[0].size();
vector<vector<int>>dp(m,vector<int>(n,0));
dp[0][0]=grid[0][0];
for(int i=1;i<m;i++)
dp[i][0]=dp[i-1][0]+grid[i][0];
for(int j=1;j<n;j++)
dp[0][j]=dp[0][j-1]+grid[0][j];
for(int i=1;i<m;i++)
for(int j=1;j<n;j++)
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
return dp[m-1][n-1];
}
};
继续优化,不开辟dp数组,直接把grid数组当dp数组使用:
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
//dp[i][j]表示从(0,0)到(i,j)能拿到的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
int m=grid.size(),n=grid[0].size();
for(int i=1;i<m;i++)
grid[i][0]=grid[i-1][0]+grid[i][0];
for(int j=1;j<n;j++)
grid[0][j]=grid[0][j-1]+grid[0][j];
for(int i=1;i<m;i++)
for(int j=1;j<n;j++)
grid[i][j]=max(grid[i-1][j],grid[i][j-1])+grid[i][j];
return grid[m-1][n-1];
}
};
class Solution {
public://滑动窗口法+双指针
int lengthOfLongestSubstring(string s) {
if (s.size() == 0)
return 0;
int left = 0,right=0;
int maxlength = 1;
//关键就是时刻要保证双指针区间内的字符串是无重复字符的
//start
right++;
//每次while循坏都会加入一个新的s[right]
while (right<=s.size()-1) {
for (int temp_left=left; temp_left < right; temp_left++)
{
if (s[right] == s[temp_left])
{
left = temp_left + 1;
break;
}
}
maxlength = max(maxlength, right - left + 1);
right++;
}
return maxlength;
}
};
// 1, 2, 3, 4, 5, 6, 8, 9, 10, 12
//除了1以外的所有丑数是由另一个丑数乘以2,3或5得到的
//三指针
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> dp(n, 0);
dp[0] = 1;
int p2 = 0, p3 = 0, p5 = 0;
for (int i = 1; i < n; i++) {
dp[i] = min(min(dp[p2] * 2, dp[p3] * 3), dp[p5] * 5);
if (dp[i] == dp[p2] * 2)
p2++;
if (dp[i] == dp[p3] * 3)
p3++;
if (dp[i] == dp[p5] * 5)
p5++;
}
return dp[n - 1];
}
};
class Solution {
public:
char firstUniqChar(string s) {
unordered_map<char,int>mp;
for(char elem:s)
{
mp[elem]++;
}
for(char elem:s)
{
if(mp[elem]==1)
return elem;
}
return ' ';
}
};
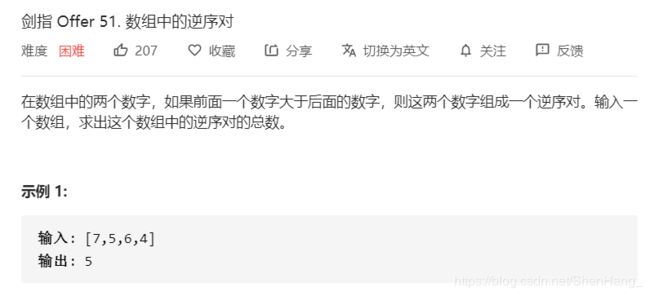
经典的归并排序问题
这题的重点就是在归并的时候统计逆序对的个数
class Solution {
//归并排序
public:
int reversePairs(vector<int>& nums) {
if(nums.size()==0)
return 0;
vector<int> temp(nums);//辅助数组
return mergeSort(nums,temp,0,nums.size()-1);
}
int mergeSort(vector<int>&nums,vector<int>&temp,int start,int end)
{
if(start==end)
return 0;
int mid=(start+end)/2;
int left=mergeSort(nums,temp,start,mid);
int right=mergeSort(nums,temp,mid+1,end);
int count=merge(nums,temp,start,mid,end);//在归并的时候统计逆序对的个数
return left+right+count;
}
int merge(vector<int>&nums,vector<int>&temp,int start,int mid,int end)//对两个有序序列[start,mid]和[mid+1,end]归并
{
int count = 0;
int first_start = start;//初始化为前半段第一个数字的下标
int second_start = mid + 1;//初始化为后半段第一个数字的下标
int copy_start = start;//初始化为辅助数组第一个数字的下标
while (first_start <= mid&&second_start <= end)
{
if (nums[first_start] <= nums[second_start])
temp[copy_start++] = nums[first_start++];
else
{
temp[copy_start++] = nums[second_start++];
count+= (mid - first_start )+ 1;//关键点(很好理解,当前的数比a小,那么由于是升序序列,所以之前的所有数一定也比a小)
}
}
//若second_start先到了后半段末尾
while (first_start <= mid)
temp[copy_start++] = nums[first_start++];
//若first_start先到了前半段末尾
while (second_start <= end)
temp[copy_start++] = nums[second_start++];
for (int i = start; i <= end; i++)
nums[i] = temp[i];
return count;
}
};
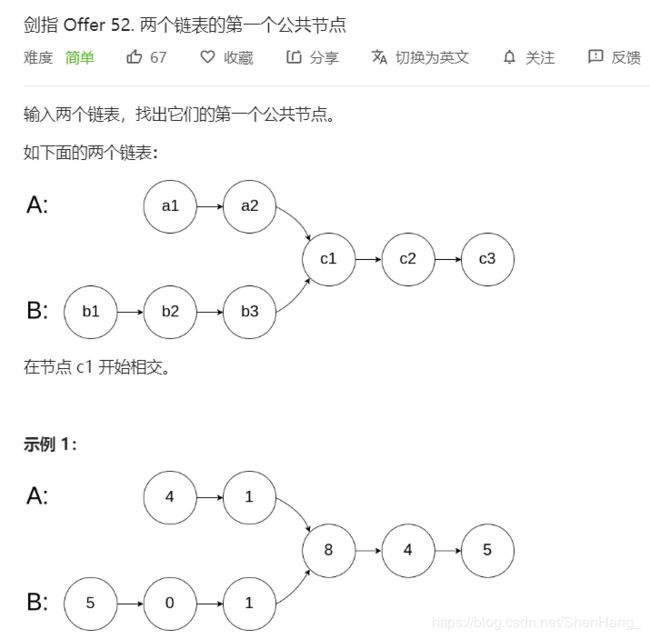
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int count_A=0;
int count_B=0;
ListNode*t_A=headA;
ListNode*t_B=headB;
while(t_A!=NULL)
{
count_A++;
t_A=t_A->next;
}
while(t_B!=NULL)
{
count_B++;
t_B=t_B->next;
}
if(count_A>=count_B)
{
int diff=count_A-count_B;
t_A=headA;
t_B=headB;
while(diff)
{
t_A=t_A->next;
diff--;
}
while(t_A!=t_B)
{
t_A=t_A->next;
t_B=t_B->next;
}
return t_A;
}
else
{
int diff=count_B-count_A;
t_A=headA;
t_B=headB;
while(diff)
{
t_B=t_B->next;
diff--;
}
while(t_A!=t_B)
{
t_A=t_A->next;
t_B=t_B->next;
}
return t_B;
}
}
};
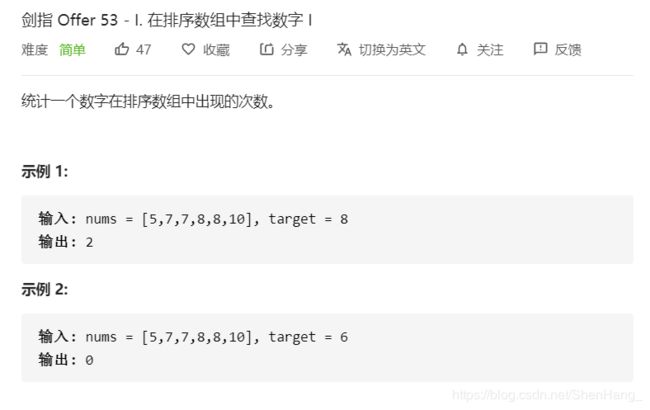
二分法找,找到后左右延伸查找即可,秒杀。
注意,这道题如果考到,面试官肯定会限制只能用二分法!
class Solution {
public:
int search(vector<int>& nums, int target) {
//这题面试官肯定限制只能用二分法
int count=0;
int low=0,high=nums.size()-1;
while(low<=high)
{
int mid=(low+high)/2;
if(nums[mid]==target)
{
count++;
for(int i=mid+1;i<nums.size();i++)
{
if(nums[i]==target)
count++;
else
break;
}
for(int i=mid-1;i>=0;i--)
{
if(nums[i]==target)
count++;
else
break;
}
return count;
}
else if(nums[mid]<target)
{
low=mid+1;
}
else
{
high=mid-1;
}
}
return count;
}
};
剑指书上给出的思路是找到第一个target对应的下标和最后一个target对应的下标:
我把这个思路也实现了一下,也很简单,代码如下:
class Solution {
public:
int search(vector<int>& nums, int target) {
//这题面试官肯定限制只能用二分法
int first_target_index = get_first_target(nums, 0, nums.size() - 1, target);
int last_target_index = get_last_target(nums, 0, nums.size() - 1, target);
if (first_target_index == -1)return 0;
return last_target_index - first_target_index + 1;
}
int get_first_target(vector<int>& nums, int low, int high, int target)
{
if (low > high)//递归结束的条件
return -1;
int mid = (low + high) / 2;
if (nums[mid] == target)
{
if ((mid - 1 >= 0 && nums[mid - 1] != target) || mid == 0)
{
return mid;
}
else//说明第一个target在左边
{
high = mid - 1;
}
}
else if (nums[mid] < target)//说明第一个target在右边
{
low = mid + 1;
}
else//说明第一个target在左边
{
high = mid - 1;
}
return get_first_target(nums, low, high, target);
}
int get_last_target(vector<int>& nums, int low, int high, int target)
{
if (low > high)//递归结束的条件
return -1;
int mid = (low + high) / 2;
if (nums[mid] == target)
{
if ((mid + 1 <= nums.size() - 1 && nums[mid + 1] != target) || mid == nums.size() - 1)
{
return mid;
}
else//说明最后一个target在右边
{
low = mid + 1;
}
}
else if (nums[mid] < target)//说明最后一个target在右边
{
low = mid + 1;
}
else//说明最后一个target在左边
{
high = mid - 1;
}
return get_last_target(nums, low, high, target);
}
};
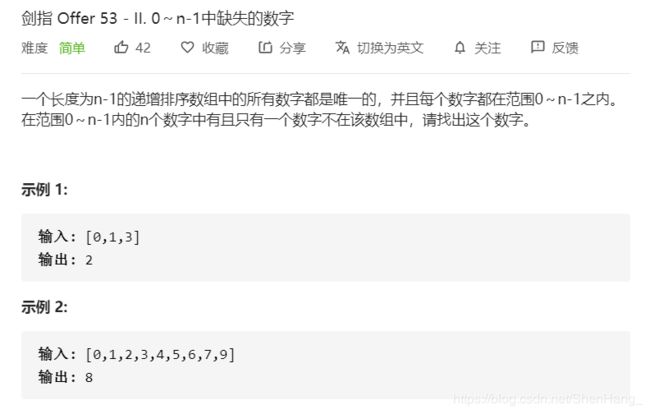
class Solution {
public:
int missingNumber(vector<int>& nums) {
int begin=0,end=nums.size();
int res=0;
for(int i=begin;i<=end;i++)
{
res^=i;
}
for(int i:nums)
{
res^=i;
}
return res;
}
};
法2:二分法,本题主要考察二分法
class Solution {
public:
int missingNumber(vector<int>& nums) {
int low=0,high=nums.size()-1;
while(low<=high)
{
int mid=(low+high)/2;
if(nums[mid]!=mid)
{
if(mid==0||(mid-1>=0&&nums[mid-1]==mid-1))//前一个元素和下标相等
{
return mid;
}
else//前一个元素和下标不相等,那么查找左边
{
high=mid-1;
}
}
else//查找右边
{
low=mid+1;
}
}
if(low==nums.size())
return nums.size();
return -1;
}
};
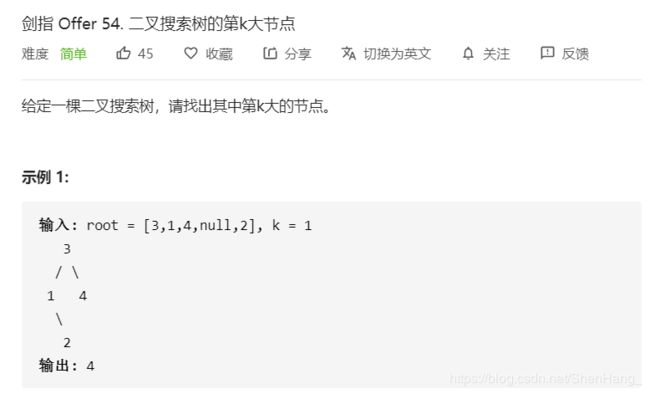
class Solution {
public:
int kthLargest(TreeNode* root, int k) {
//中序遍历(按右根左)
if(root==NULL||k<=0)return -1;
DFS(root,k);
return res;
}
void DFS(TreeNode*root,int&k)
{
if(root==NULL||res!=-1)
return;
DFS(root->right,k);
k--;
if(k==0)
{
res=root->val;
return;
}
DFS(root->left,k);
}
private:
int res=-1;
};
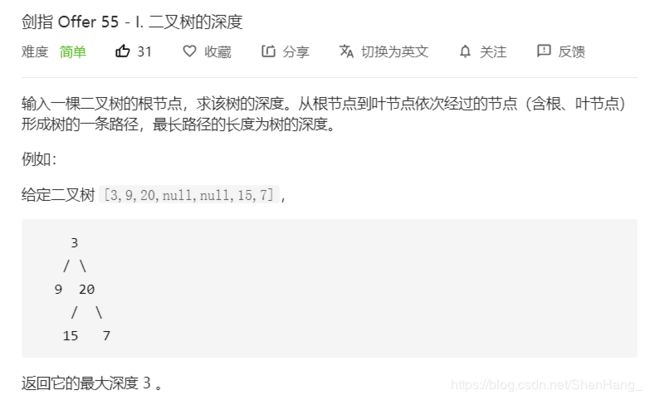
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==NULL)return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
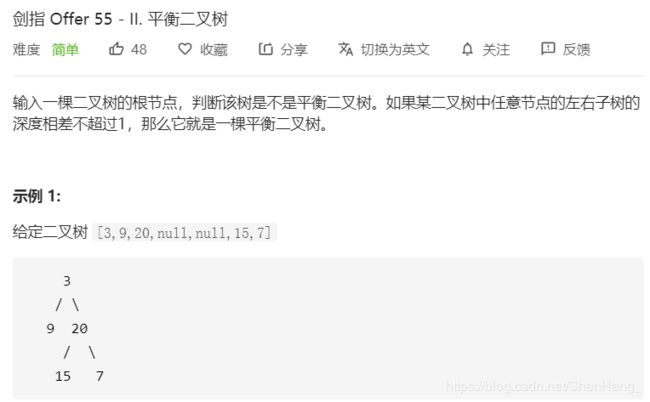
重点题,不同方法效率不同!!!
法1:正常思路(发现某些结点会被重复遍历,效率不高)
class Solution {
public:
bool isBalanced(TreeNode* root) {
if(root==NULL)return true;
int left=depth(root->left);
int right=depth(root->right);
int diff=abs(left-right);
if(diff>1)
return false;
return isBalanced(root->left)&&isBalanced(root->right);
}
int depth(TreeNode*root)
{
if(root==NULL)
return 0;
return max(depth(root->left),depth(root->right))+1;
}
};
法2:自下而上递归,在DFS的形参中加一个变量,记录当前树的深度
class Solution {
public:
bool isBalanced(TreeNode* root) {
if(root==NULL)return true;
int depth;
return DFS(root,depth);
}
bool DFS(TreeNode*root,int&depth)//判断当前树是否平衡,并记录树的深度
{
if(root==NULL)
{
depth=0;
return true;
}
int left,right;
if(DFS(root->left,left)&&DFS(root->right,right))
{
int diff=abs(left-right);
if(diff<=1)
{
depth=max(left,right)+1;
return true;
}
}
return false;
}
};
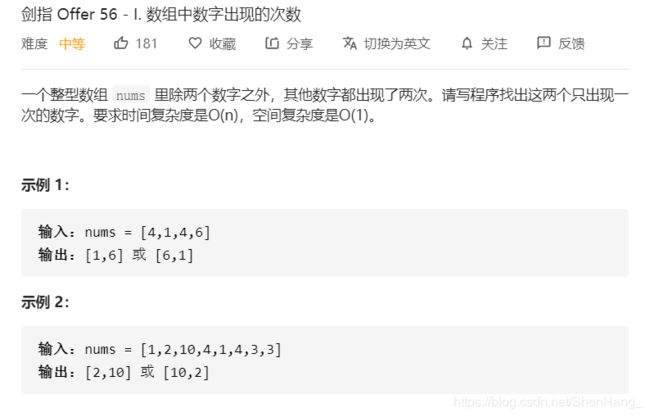
如果两个数不相同,那么它们必定至少在某一个bit是不同的。
利用这一特点,使用异或,把两个要找的数分在不同的两堆中。
class Solution {
public:
vector<int> singleNumbers(vector<int>& nums) {
int length = nums.size();
if (length <= 1)
return{};
int result_ExclusiveOR = 0;
for (int i = 0; i < length; i++)
{
result_ExclusiveOR ^= nums[i];
}
unsigned int index = find_first_index_of_bit_1(result_ExclusiveOR);
vector<int>res;
int temp1 = 0;
int temp2 = 0;
for (int i = 0; i < length; i++)
{
if (IsBit1(nums[i], index))//把两个要找的数分在不同的两堆中
{
temp1 ^= nums[i];
}
else
{
temp2 ^= nums[i];
}
}
res.push_back(temp1);
res.push_back(temp2);
return res;
}
int find_first_index_of_bit_1(int number)//找到number中第一个为1的位
{
unsigned int index = 0;
while ((number & 1) == 0)//再次注意:==的优先级比&高
{
index++;
number = number >> 1;//右移一位
}
return index;
}
//判断第index位是否为1
bool IsBit1(int num, unsigned int index)
{
num = num >> index;//右移index位
return(num & 1);
}
};
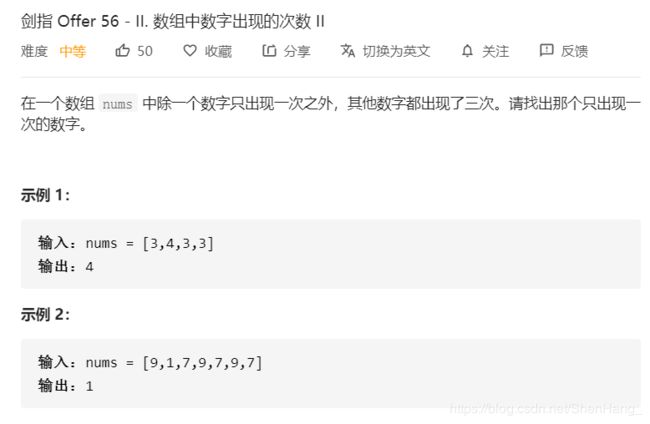
这题我不想使用位运算来做(这种技巧性太强,感觉意义不大),还是直接用map吧。
class Solution {
public:
int singleNumber(vector<int>& nums) {
map<int,int>mp;
for(int elem:nums)
{
mp[elem]++;
}
for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++)
{
if((*it).second==1)
{
return (*it).first;
}
}
return -1;
}
};
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
//简单双指针
vector<int>res;
int i=0,j=nums.size()-1;
while(i<j)
{
if(nums[i]+nums[j]==target)
{
res.push_back(nums[i]);
res.push_back(nums[j]);
return res;
}
else if(nums[i]+nums[j]>target)
{
j--;
}
else
{
i++;
}
}
return res;
}
};
class Solution {
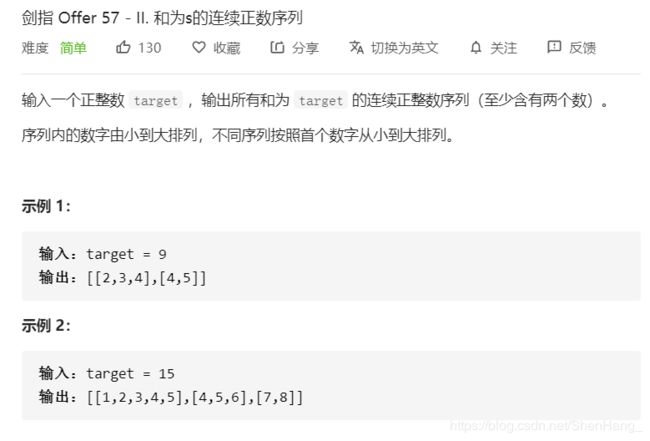
public:
vector<vector<int>> findContinuousSequence(int target) {
int i = 1; // 滑动窗口的左边界
int j = 1; // 滑动窗口的右边界
int cur_sum = 1; // 滑动窗口中数字的和
vector<vector<int>> res;
while (i <= target / 2)
{
if (cur_sum < target)
{
// 右边界向右移动
j++;
cur_sum += j;
} else if (cur_sum > target)
{
// 左边界向右移动
cur_sum -= i;
i++;
} else
{
// 记录结果
vector<int> temp;
for (int k = i; k <= j; k++)
temp.push_back(k);
res.push_back(temp);
// 左边界向右移动(关键点)
cur_sum -= i;
i++;
}
}
return res;
}
};
class Solution {
public:
string reverseWords(string s) {
//删除字符串头部和尾部的空格
int left = 0, right = s.size() - 1;
while (left < s.size() && s[left] == ' ')left++;
while (right >= 0 && s[right] == ' ')right--;
if (left > right)return "";
s = s.substr(left, right - left + 1);
//删除中间的空格,只保留一个
for (int i = 0; i < s.size(); i++)
{
if (s[i] == ' ')
{
while (s[i + 1] == ' ')
{
s = s.erase(i + 1, 1);
}
}
}
//再整体翻转
reverse(s.begin(), s.end());
int len = s.size();
//尾部加个空格,再逐个单词翻转
s += ' ';
int mark = 0;
//根据空格,翻转每个单词
for (int i = 0; i < len + 1; i++)
{
if (s[i] == ' ')
{
Reverse(s, mark, i - 1);
mark = i + 1;
}
}
//最后去掉添加的空格
s = s.substr(0, len);
return s;
}
void Reverse(string&str, int begin, int end)
{
while (begin < end)
{
swap(str[begin++], str[end--]);
}
}
};
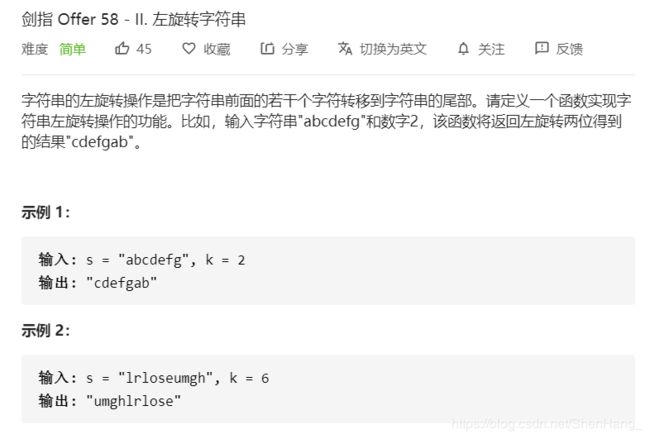
class Solution {
public:
string reverseLeftWords(string s, int n) {
//先反转前一段字符串,再反转后一段字符串,最后反转整个字符串
Reverse(s,0,n-1);
Reverse(s,n,s.size()-1);
Reverse(s,0,s.size()-1);
return s;
}
void Reverse(string&s,int start,int end)
{
while(start<end)
{
swap(s[start++],s[end--]);
}
}
};

重点题!如果要求不能用暴力法,要求线性的时间复杂度,那么就是一道难题了!

代码如下:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int>res;
deque<int>my_deque;
for (int i = 0; i < nums.size(); ++i)
{
while (!my_deque.empty() && nums[my_deque.back()] <= nums[i])//维护递减序列
my_deque.pop_back();
while (!my_deque.empty() && my_deque.front() < i - k + 1)//维护范围[i-k+1,i]
my_deque.pop_front();
my_deque.push_back(i);
if (i >= k - 1)
res.push_back(nums[my_deque.front()]);
}
return res;
}
};

和上一题一样,核心就是当一个元素进入队列的时候,它前面所有比它小的元素就不会再对答案产生影响。
class MaxQueue {
public:
//当一个元素进入队列的时候,它前面所有比它小的元素就不会再对答案产生影响。
//举个例子,如果我们向队列中插入数字序列 1 1 1 1 2,那么在第一个数字 2 被插入后,数字 2 前面的所有数字 1 将不会对结果产生影响。因为按照队列的取出顺序,数字 2 只能在所有的数字 1 被取出之后才能被取出,因此如果数字 1 如果在队列中,那么数字 2 必然也在队列中,使得数字 1 对结果没有影响。
deque<int>data;
deque<int>maximums;
MaxQueue() {
}
int max_value() {
if(maximums.empty())
return -1;
return maximums.front();
}
void push_back(int value) {
//把之前所有比当前元素小的全部移除
while(!maximums.empty()&&maximums.back()<value)
{
maximums.pop_back();
}
data.push_back(value);
maximums.push_back(value);
}
int pop_front() {
if(data.empty())
return -1;
int temp=data.front();
if(data.front()==maximums.front())
{
maximums.pop_front();
}
data.pop_front();
return temp;
}
};
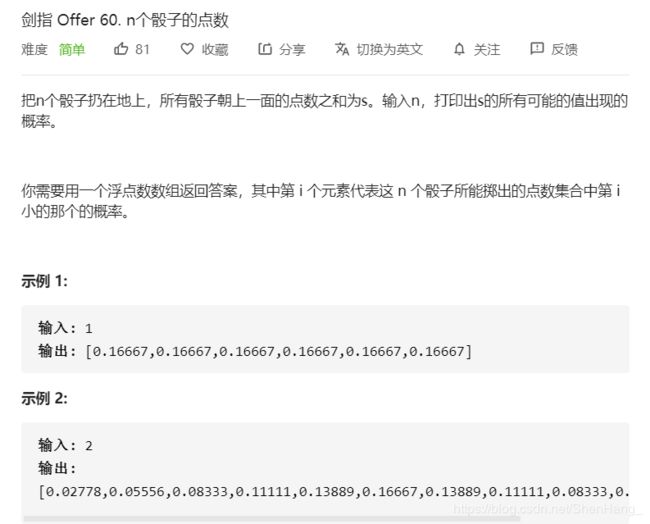
class Solution {
public:
vector<double> twoSum(int n) {
//dp[i][j]表示i个骰子投出的和为j一共可以发生的次数
//dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]+dp[i-1][j-4]+dp[i-1][j-5]+dp[i-1][j-6]
vector<vector<int>>dp(n+1,vector<int>(6*n+1,0));//先全部置为0
for(int i=1;i<=6;i++)
dp[1][i]=1;
for(int i=1;i<=n;i++)
for(int j=i;j<=6*n;j++)
{
for(int k=1;k<=6;k++)
{
if(!(j>=i&&j-k>=i-1))
break;
dp[i][j]+=dp[i-1][j-k];
}
}
vector<double>res;
for(int i=n;i<=6*n;i++)
res.push_back(dp[n][i]/pow(6,n));
return res;
}
};
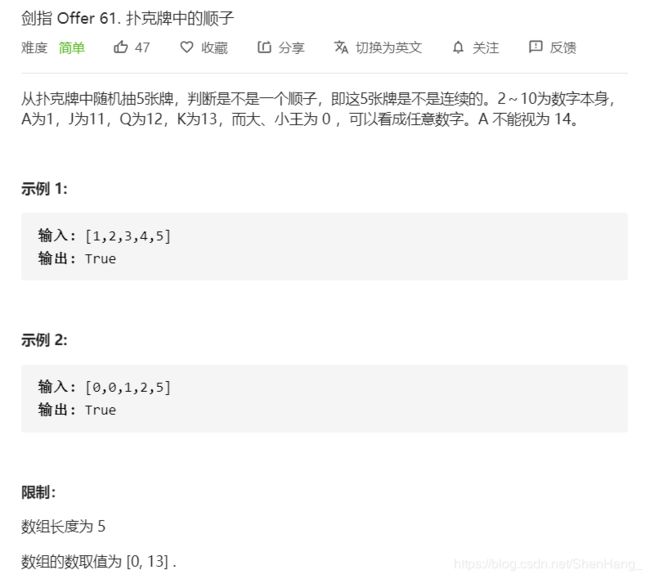
class Solution {
public:
bool isStraight(vector<int>& nums) {
//先排序
sort(nums.begin(),nums.end());
int numberOfZero=0;
int numberOfGap=0;
for(int i=0;i<nums.size()&&nums[i]==0;i++)
numberOfZero++;
for(int i=numberOfZero;i<nums.size();i++)
{
if(i+1<nums.size()&&nums[i]==nums[i+1])//对子不能有
return false;
if(i+1<nums.size()&&nums[i]+1!=nums[i+1])
{
numberOfGap+=nums[i+1]-nums[i]-1;
}
}
return numberOfZero>=numberOfGap;
}
};

这题如果用数学的方法技巧性太强,所以还是用循环链表来做(leetcode不能AC)
class Solution {
//循环链表
public:
typedef struct Node
{
Node*next;
int val;
Node(int i):next(NULL),val(i){}
}Node;
int lastRemaining(int n, int m) {
if(m==1)return n-1;
Node*head=create(n);
Node*cur=head;
while(cur->next!=cur)
{
for(int i=1;i<=m-2;i++)
cur=cur->next;
//删除下一个结点
Node*temp=cur->next->next;
delete cur->next;
cur->next=temp;
//下一轮
cur=cur->next;
}
return cur->val;
}
Node*create(int n)//创建循环链表
{
Node*dummy=new Node(-1);
Node*prev=dummy;
for(int i=0;i<n;i++)
{
Node*cur=new Node(i);
prev->next=cur;
prev=cur;
}
prev->next=dummy->next;//闭环
return dummy->next;
}
};
class Solution {
public:
int maxProfit(vector<int>& prices) {
//思路就是遍历的时候用一个变量存储之前数据的最小值
if(prices.size()==0)return 0;
int prev_min=prices[0];
int res=INT_MIN;
for(int i=1;i<prices.size();i++)
{
res=max(res,prices[i]-prev_min);
prev_min=min(prev_min,prices[i]);
}
return res<0?0:res;
}
};
class Solution {
public:
int sumNums(int n) {
n && (n += sumNums(n-1));//利用&&的短路原则和递归
return n;
}
};
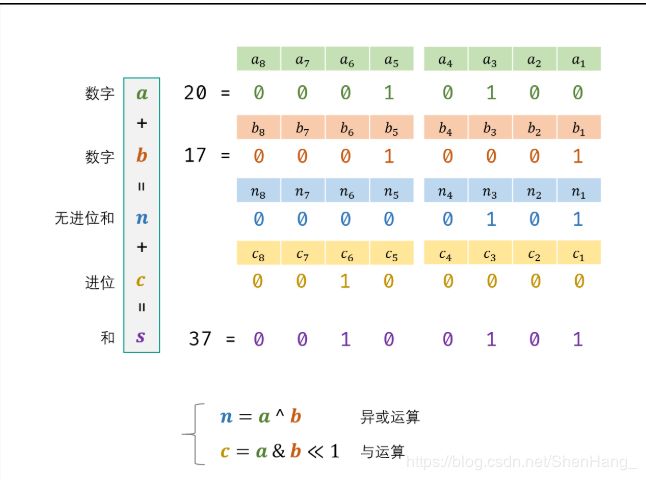
class Solution {
public:
//0+0=0,0+1=1,1+1=0;
//0^0=0,0^1=1,1^1=0
int add(int a, int b) {
while(b!=0)
{
int c=a^b;//c是进位
b=((unsigned int)(a&b)<<1);
a=c;
}
return a;
}
};
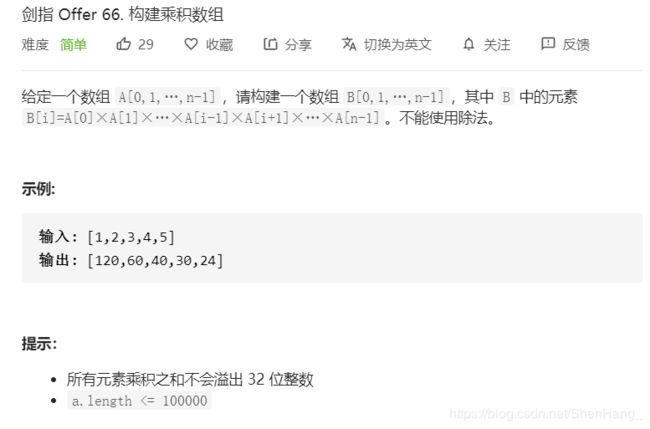
class Solution {
public:
vector<int> constructArr(vector<int>& a) {
int length=a.size();
vector<int>res(length);
if (length == 0)
return res;
res[0] = 1;
for (int i = 1; i < length; i++)//从第二个元素开始直到最后一个元素
res[i] = res[i - 1] * a[i - 1];//从前往后卷积
int temp = 1;
for (int i = length - 2; i >= 0; i--)//从倒数第二个元素开始直到首元素
{
temp *= a[i + 1];//从后往前卷积
res[i] *= temp;
}
return res;
}
};
class Solution {
public:
int strToInt(string str) {
int i = 0;
long long num = 0;
if (str.size()!=0)
{
while (str[i] == ' ')
i++;
int zf = 0;
bool minus = false;
if (str[i] == '+')
{
i++;
zf++;
}
if (str[i] == '-')
{
i++;
minus = true;
zf++;
}
if (zf > 1)
return 0;
while (i<str.size())
{
if (str[i] >= '0'&&str[i] <= '9')
{
if (!minus)
num = num * 10 + (str[i] - '0');
else
num = num * 10 - (str[i] - '0');
if ((!minus&&num > (signed int)0x7FFFFFFF))//考虑int型溢出
{
num = 0x7FFFFFFF;
break;
}
else if ((minus&&num < (signed int)0x80000000))
{
num = 0x80000000;
break;
}
i++;
}
else
break;
}
}
return (int)num;
}
};
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL)
return NULL;
if(root->val>p->val&&root->val>q->val)//说明p,q都在左子树
return lowestCommonAncestor(root->left,p,q);
else if(root->val<p->val&&root->val<q->val)//说明p,q都在右子树
return lowestCommonAncestor(root->right,p,q);//说明p,q一个在左子树,一个在右子树
else
{
return root;
}
}
};
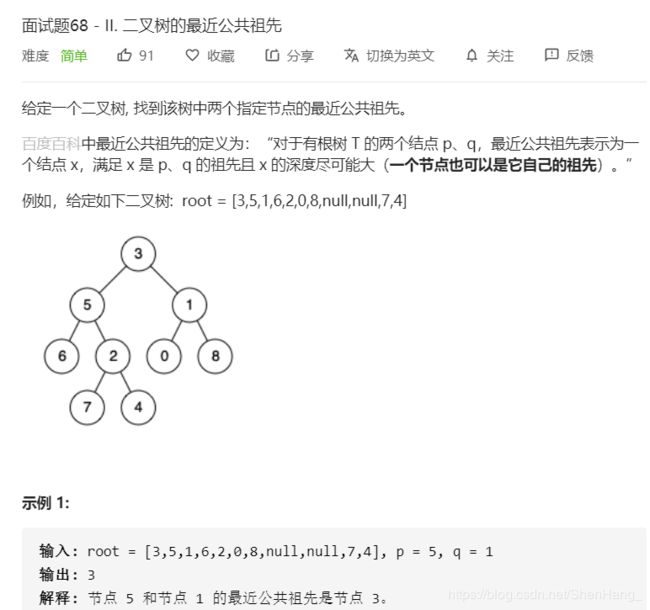
这题是非常好的递归题!!,和上一题唯一的区别在于,本题就是普通的二叉树
当我们用递归去做这个题时不要被题目误导,应该要明确一点
这个函数的功能有三个:
1.如果p和q都在当前树中,则返回它们的最近公共祖先;
2.如果当前树中只存在一个,则返回存在的那个;
3.如果当前树中,p和q都不存在,则返回NULL;
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL)//递归结束的条件
return NULL;
if(root==p || root==q)//递归结束的条件
return root;
TreeNode*left=lowestCommonAncestor(root->left,p,q);
TreeNode*right=lowestCommonAncestor(root->right,p,q);
if(left&&right)//说明p,q一个在左子树,一个在右子树
return root;
if(left)//说明p,q都在左子树
return left;
if(right)//说明p,q都在右子树
return right;
return NULL;
}
};