现代语音信号处理之语谱图（spectrogram）

语谱图就是语音频谱图，一般是通过处理接收的时域信号得到频谱图，因此只要有足够时间长度的时域信号就可。（时间长度为保证频率分辨率）
专业点讲，那是频谱分析视图，如果针对语音数据的话，叫语谱图。语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量。由于是采用二维平面表达三维信息，所以能量值的大小是通过颜色来表示的，颜色深，表示该点的语音能量越强。
可是为什么采用二维平面来表示三维信息呢？这个是有历史原因的。在数字技术发展以前，人们可视化研究语音数据的方法是把数据通过频率滤波器，然后各个频率的数据驱动相应的类似针式打印的设备按频率高低顺序记录在一卷纸上，信号的强弱由记录在纸上的灰度来表示。记录纸按照一定的速度旋转，即相当于在不同的时间里记录下语音数据。
语谱图还分为窄带语谱图和宽带语谱图。
“窄带”，顾名思义，带宽小，则时宽大，则短时窗长，窄带语谱图就是长窗条件下画出的语谱图。“宽带”，正好相反。至于“横竖条纹”，窄带语谱图的带宽窄，那么在频率上就“分得开”，即能将语音各次谐波“看得很清楚”，即表现为“横线”。“横”就体现出了频率分辨率高。分辨率可以直观的看做“分开能力”。“频率分辨率”高就是在频率上将各次谐波分开的能力高，表现为能分辨出各次谐波的能力高，频率分辨率越高，越容易分辨各次谐波。类似的，宽带语谱图的时宽窄，那么在时间上就“分得开”，即能将语音在时间上重复的部分“看得很清楚”，即表现为“竖线”。“竖”就体现出了时间分辨率高。时间分辨率越高，谱图上的竖线看得越清楚。图1和图2分别示出了一条语音句子的窄带语谱图和宽带语谱图。短时窗长度分别是20ms和2ms。

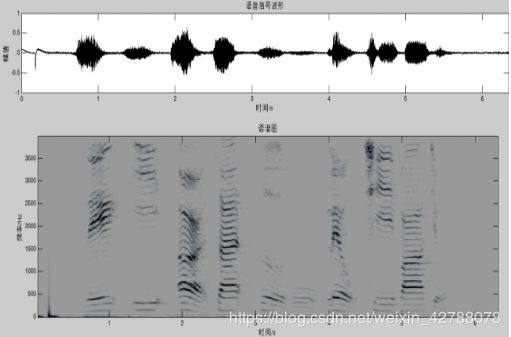
图1是一条语音及其窄带语谱图。上图是语音时间波形，下图是上图的窄带语谱图

图2同一条语音及其宽带语谱图。上图是语音时间波形，下图是上图的宽带语谱图

图1虚框框住的部分就是一条横条纹，整个谱图中有非常多的这种横条纹。图2虚框框住的部分，在小图中清晰的显示出了一条一条的“竖线”，被框住的有27条竖线。

信号的语谱图

语音中设计窗函数，窗函数性质大同小异，这里以窗函数为对象进行分析。
对于时域的窗函数：

其表达式为：

对应的傅里叶变换：

表达式为：

可见信号的时宽越大（小），信号的频带宽度越小（大），对于矩形窗，有着带宽B与时宽乘积为这样的特性，其他窗函数也有着类似的性质。

MATLAB仿真举例：

x=zeros(1,2000);%序列长度指定为2000
x(100:140)=1;%矩形窗为40个点
y=fft(x);
y=abs(y);
plot(1:length(x),fftshift(y)/max(y),'k','linewidth',2)
title('频谱响应函数')

根据上面的分析，信号长度定为2000（即2*pi的长度）的话，矩形窗为40，要满足时宽与带宽乘积为2000不变，理论上带宽应为50，一下的结果图验证了上面的理论：

由于语音信号具有短时平稳特性，因此对其分析时，要进行加窗处理，借助上面的分析，可以看出，窗长如果选择短一些的话，就是时宽较小，对应的带宽就要大一些，在这种情况下得到的就是宽带语谱图，反之则得到窄带语谱图。

窄带语谱图

对于一段语音进行分析（语音内容为0 1 2 3 4 5 6 7 8 9），语音采样率为8000Hz,取窗长为512个数据点，帧移为窗长的1/4，即128个数据点。

得到如下结果图：

从结果图中可以清楚看到谐波的结构，频率分辨率非常好，但是时间上的分辨率就不理想。对于上述语音，画出其频率特性：

语音低频部分（红线）体现了声道的特性，窄带语谱图，频率分辨率太过精细，不能很好体现出共振峰的大致位置，即反映不出基波的变化特性。

宽带语谱图

对于一段语音进行分析（语音内容为0 1 2 3 4 5 6 7 8 9），语音采样率为8000Hz,取窗长为128个数据点，帧移为窗长的1/4，即32个数据点。

得到如下结果图：

与窄带语谱图相反，宽带语谱图的时间分辨率很好，频率分辨率较低，不能很好反映声音的纹理特性，反映了频谱的时变特性，能很好分辨出共振峰的大致位置，但分辨不清谐波结构。

从窄带语谱图和宽带语谱图看基音频率和共振峰

基音周期表示声带的震动周期，每隔这么长时间（震动周期），有一个气流通过，“每隔”就体现了周期性，这就是基音周期，那么谱图上就应该有这个频率的信号分量，而且这个频率的幅度（能量）不应该很小，因为每隔一段时间“就有”一团能量通过声带。所以基音频率所在的成分在窄带语谱图上应该是所有横条纹中频率范围最低的那条。在图1中，用虚线框框住的部分就表示基音频率成分，与其在同一水平线上的条纹都表示该时刻的基音频率成分，这条条纹对应的纵轴刻度值就表示基音频率。从图1小图可估计基音频率大约在250Hz左右，基音频率略有波动，0.5s处大约是240Hz。其他横条纹就是各次谐波，这些谐波中有些地方颜色比同时刻其附近其他横条纹颜色要深，这些颜色深的条纹表示共振峰。有些时刻，颜色较局部附近深的条纹不止一条，这些深色条纹组成了各次共振峰，如第一、第二、第三共振峰。图2，宽带语谱图的基音频率和共振峰就不清晰了。但是其仍可以看出基音周期，图2小图具有明显的竖线，两条竖线之间的时间就表示基音周期。在0.44s到0.54s时间段内大约有25条竖线，即24个间隔，则基音周期可估计为（0.54-0.44）/24=4.17ms，则基音频率估计为240Hz。

从语音时域波形上估计基音周期、频谱曲线上估计基音频率

选取0.5s处的一段语音片段，长度为20ms。其时域波形和频谱如图3。

图3 0.5s处语音片段时域波形及其频谱
图3左图，用红圈圈示的尖峰用于估计基音周期，双向箭头表示时间范围内5个圈共4个相似的波段，这4段就表示4个基音周期，则可估计基音周期约为4.25ms，则基音频率约为235.2941Hz。图3右图，频谱具有明显小尖峰，这些尖峰在低频部分（可认为语音频率3400Hz内）比较有规律且平滑，高频出现小幅度的“杂乱”，这些“杂乱”表示噪声，来源有录音设备及量化噪声等（虽然幅度很小，甚至根本就“听”不出来，但存在是事实）。这些尖峰就是各次谐波，从左往右一次是1次、2次、3次……谐波。其中最左边的尖峰对应基音频率，其横坐标对应的值表示基音频率，从小图可看到大约为234.83Hz。利用各次谐波可以得到更精确的估计，图中用红圈表示用于估计基频的谐波，共选取了15个，估计出基频为234.8337Hz。

从语音频谱曲线上看共振峰

基音频率体现的是声源的信息，而共振峰体现的是声道的信息。为便于比较和观察，将图3这个语音片段的源和系统分离，分别展示源的频谱和声道的频谱，观察一致性。图4、5显示的是源的频谱、声道的频谱、语音的频谱及共振峰的位置信息，图5去掉了小图。粉红线是源信息的频谱，红线是语音的频谱，黑色虚线是语音频谱的包络，蓝线是声道频谱，蓝色圈圈标示出声道频谱的峰值点，粉红虚竖线显示这些峰值点的位置。根据语音产生的源-滤波器模型及源、系统的卷积解释，语音频谱的包络显示的是声道的信息，而小尖峰显示源的信息，如谐波。可看到粉红线和红线二者的峰值的位置正好一一对应，体现了源的信息，而且粉红线（源）明显没有包络峰值，说明声道的信息被滤除。同样，蓝线没有了小尖峰，即滤掉了源的信息。并且声道的峰值点位置与语音频谱包络的峰值位置也正好一一对应。蓝圈圈的个数表示共振峰的个数，共有4个，从左至右分别称为F1、F2、F3、F4，（F0是基音频率）。它们横轴值表示共振峰频率值，某共振峰带宽就表示该共振峰所占频带宽度。这个图还暗示了另一个有趣的事实，源所占的频率范围和声道所占的频率范围是一样的，在频域利用高通或低通或带通的方法分离源和系统是行不通的。

图4语音片段时域波形及其源、声道和语音频谱。

图5语音片段时域波形及其源、声道和语音频谱。去掉小图（小图遮挡了部分信息）

基音频率和共振峰是能从谱图、频谱上看出来的语音的最基本的信息，当然可以看出其他更多的信息。比如，窄带语谱图上基本上可以发现，低频部分，横条纹比较直，而高频部分，条纹变“弯”了，这表示什么？图1小图可明显看到，基音频率也不是不变的，其也具有波动，我们可以人为的将基频线连接起来为一条曲线，这称为基音跟踪。共振峰表示“谐振”，频谱上表示为频谱包络（其实是上包络）的峰值，那么频谱下包络的谷值点就表示“反谐振”。频谱的“尖峰”显示的是源的信息，小尖包突起是周期性的，是有用的，那么“杂乱”的源头是非周期性的，这在语音转换中是一种很重要的信息。