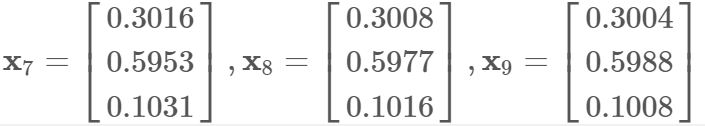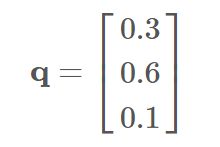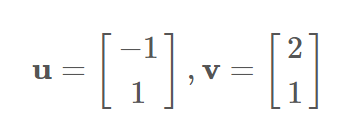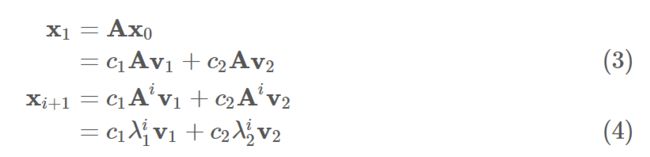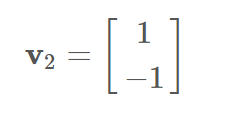线性代数拾遗(六):特征值与特征向量
![]()
线性代数拾遗(一):线性方程组、向量方程和矩阵方程
线性代数拾遗(二):线性方程组的解集及其几何意义
线性代数拾遗(三):线性变换以及矩阵的意义
线性代数拾遗(四):线性方程组的应用
线性代数拾遗(五):矩阵变换的应用
上一章最后,我们引入了马尔可夫链。马尔可夫链简单来说就是一个个状态组成的链,其中每个状态只于前一个状态有关。然而,除了这个简单定义之外,马尔可夫链还有一个有趣的性质:平稳分布。要解释平稳分布是什么,我们先从一个例子讲起。
一、马尔可夫链的平稳分布
比如一个地区有三个政党:「民主党」、「共和党」、「自由党」,我们用一个向量 x∈R3 来表示每年选举的投票结果:
假设每年的选举结果只和上一年的结果有关,即选举向量构成的序列满足马尔可夫性质,是一个马尔可夫链。那么,像 上一章 那个人口迁移的例子一样,我们可以用一个状态迁移矩阵来描述每年选举结果的变化情况。
比如我们要研究某一年开始,该地区选举变化情况,而且已经得到了该地区选举变化的迁移矩阵P:
假设在起始年,三个党的得票情况为:
那么我们顺着迁移矩阵看一下接下来几年,这个地区的选举情况会发生怎么样的变化。通过递推公式
我们可以计算出
……
……
我们可以发现,这个选举结果向量x越来越逼近于向量
事实上,当我们把迁移矩阵乘上这个向量:
就会发现,不但选举结果越来越趋向某一个固定向量q,而且当结果达到和q一致时,这个系统便不再改变!这也就是我们所说的达到平稳分布。这个固定向量q就是 稳态向量。
可以证明,这个稳态向量由迁移矩阵所控制。一个马尔可夫链中,迁移矩阵一旦确定,那么不管它的起始状态(x0)是什么样,它的稳态将唯一确定(有种宿命论的感觉)。这是马尔可夫链的一个重要性质,对于一个系统的长期发展很有帮助。此外,这个性质也反应了矩阵的两个重要属性:特征值与特征向量。
二、特征值与特征向量
当我们把一个矩阵看作是一个线性变换:x↦Ax时,我们将矩阵理解成为一种运动,一种能使向量x向着向量Ax移动的“力”。一般来说,向量x经A进行变换有可能是朝着各个方向移动。然而,总有某些特殊向量,线性变换在这些向量上的作用是十分简单的。
比如:已知向量
矩阵
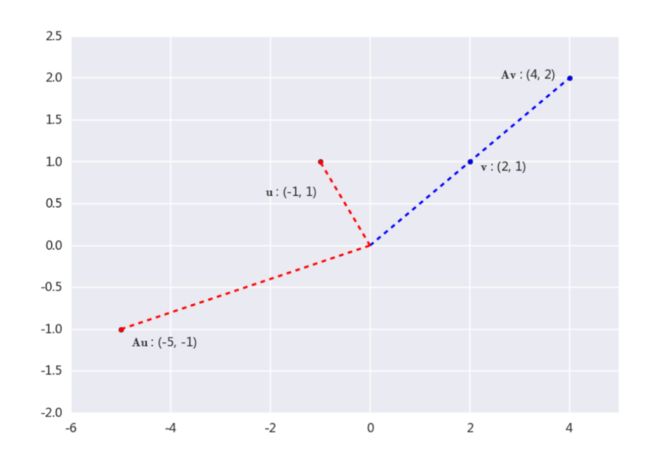
表示的线性变换分别应用于(即矩阵左乘)向量u和v后的结果如下图所示:
事实上,Av=2v,从图像上看就是拉伸了向量v。
更一般的,> A为n×n矩阵,x为非零向量,若存在数λ使得 Ax=λx,则称λ为矩阵A的特征值,x为A对应于特征值λ的特征向量。
这就是我们其实已经很熟悉的特征值与特征向量定义了。特征值与特征向量的一个作用就是来研究线性变换中那些“特殊情况”,这些特殊情况可以看作是这个线性变换的“特征”。当我们把矩阵看作线性变换时,特征值与特征向量可以相配合作为描述这个线性变换的一个“特征”(有的文献也把特征值与特征向量称为本征值与本征向量)。
至于特征值和特征向量的求解,相信大家比较熟练了(建立特征方程 (A−λI)x=0进行求解),这里不再赘述。注意,一个特征方程所有解的集合构成了一个空间,即对于某一个特征值,它所对应的特征向量将构成一个空间,被称为A对应于λ的特征空间,特征空间由零向量和所有对应于λ的特征向量组成。
不同特征值对应的特征向量线性无关,而同一个特征值对应的不同特征向量能张成整个特征空间。如果一个特征值只对应一个特征向量,那么这个特征值对应的特征空间就是一条一维直线;而如果一个特征值对应两个特征向量,那么这个特征值对应的特征空间将是一个二维平面。
由于 Ax=λx,因而线性变换A对于特征空间只起到“扩张”的作用(扩张后还是同样的特征空间)。
三、特征向量与马尔可夫链
我们已经知道 xi+1=Axk,而如果我们找一个A的特征值λ及其对应的特征向量 x0,则有
因此,如果我们已经知道一个马尔可夫链的转移矩阵 A,我们不需要看它的初始状态是什么,只要找A的特征值 λ及其对应的特征向量 x0,那么我们就能通过计算得到这个马尔可夫链达到稳态时的状态。
x0除了用一个特征向量外,也可以用多个特征向量的线性组合。比如 的特征值为 λ1,λ2,对应的两个特征向量为v1,v2,那么我们可以用c1v1+c2v2
来表示x0。这样得到的xi+1为:
3.1 人口迁移例子
回顾 上一章 那个关于城市人口迁移的研究,那个例子我们引入了马尔可夫链这个概念,而从这章我们知道马尔可夫链有个平稳分布的性质,那么上一章那个人口迁移的例子最终也一定会达到某种稳定状态,即城乡人口比例保持不变。
上一章
中,我们已经得出:
即迁移矩阵
这次的套路是求解特征方程(A−λI)x=0(事实上,这里的2阶方阵通过计算行列式解detA=0会更方便些。当然,手边有电脑的话直接交给 matlab、python 之类的就行 :D),得到特征值为 1 和 0.92,对应的特征向量分别为
和
的倍数。
由于有两个互不相等的特征值,我们可以知道它们对应的两个特征向量也线性无关,我们将初始向量 x0 用两个特征向量的线性组合表示:
假设我们已知
那么就可以解得 c1=0.125,c2=0.225。
所以,每年的人口分布为:
这就显示了这个马尔可夫链最终总会达到平稳分布,达到平稳分布时的稳态向量就是 0.125v1。这也印证了我们之前的观察:马尔可夫链达到平稳分布时,稳态向量与初始状态无关,只与迁移矩阵(特别是迁移矩阵的特征向量)有关。
总结
这一章,我们通过马尔可夫链了解到了矩阵特征值与特征向量的概念。在本章中,我们把一个矩阵看作是一个线性变换,这个矩阵不断应用于某一个向量,使这个向量在空间中发生“运动”。而直观的讲,特征值与特征向量就是来描述这个“运动”的一个“本征”的,即在某些方向上的线性变换不会改变向量的方向。
# 参考文献
线性代数及其应用:第3版/(美)莱(Lay, D.C.)著;沈复兴等译. ——北京:人民邮电出版社,2007.7
————
编辑 ∑Gemini
来源:http://mengqi92.github.io/
![]()
☞一盘红烧肉告诉你:本科、硕士、博士,区别在哪儿?
☞现代数学确实在改变世界
☞数学家们的故事
☞经典 | 奇异值分解(SVD) 的 几何意义
☞算法你都懂_如何一年赚它几百万
☞他的科学生涯堪称加速器,30岁当博导,38岁当选中科院院士,40岁当选德国科学院院士。。。
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]