专题六 字符串匹配 ：KMP、 exkmp、BM、Sunday算法总结结

个人建议

建议学习字符串匹配的时候多在纸上画，这样会节约很多时间，也有利于理解。

参考来源

https://www.cnblogs.com/zhangtianq/p/5839909.html 这篇文章讲的kmp很好，适合入门。
http://www.cnblogs.com/zjp-shadow/p/10139818.html#caioj-1461-exkmp exkmp
https://www.jianshu.com/p/dd1b59441e2e
https://blog.csdn.net/LaoJiu_/article/details/61622612?utm_source=blogxgwz7

KMP能解决的问题类型

许多的字符串的匹配问题，例如
1、（单模式匹配）文本串中是否存在连续子串与模式串相同。
2、字符串前后缀匹配
3、字符串的循环节（next数组中 length - next[ length ]即为最小循环节的长度）
4、字符串的前中后缀匹配（HDU 4763）

还有很多类型的题目，跟字符串有关的问题都可以尝试运用一下这方面的知识。

个人理解

现假设有长度为m的文本串，长度为n的模式串，我们要判断文本串是否含有模式串（连续的）。
我们这里用 i 做文本串的下标，用 j 做模式串的下标。

其他算法的不可行性
如果暴力匹配，花费的时间太长，时间复杂度为O(mn)，所以选择用更优的KMP算法。

KMP算法的优势之处
笼统的讲 , KMP算法就是在匹配时，让 i 的位置和 j的位置 不会像暴力那样，遇到不匹配的就又跑到前面去。KMP算法会根据next数组的信息，在遇到不匹配的时候，让 i 永远不往前移动，而让 j 往前跑时，往前移动尽可能小的距离（这句话等价于，不匹配时i不动，而模式串根据next数组的信息，尽可能多的往后移动）。

其中next是我们预处理所得到的数组，反观暴力算法，每次遇到不匹配的字符后，都是把模式串往后移动一位， i 和 j 放到模式串的开头。而利用next数组，我们可以少往前面走，从而让时间复杂度从O(mn)降低到O(m+n)。

求最长公共前缀后缀。
在求next数组之前，我们需要先求最长公共前缀后缀，才能求得next数组。

最长公共前缀后缀的求法：看字符串的前缀和后缀，从前缀的第一个字符与后缀的第一个字符比较，知道前缀和后缀的末尾，如果这个前缀和后缀完全相同，那么很棒，我们当前部分字符串的最长的前缀后缀。

举个例子：模式串abcdab
从头到尾遍历
第一次 a 等于 0
第二次 ab 所有的前缀后缀都不一样 结果为0
第三次 abc 还是所有的前缀后缀都不一样 结果为0
第四次 abcd 所有的前缀后缀都不一样 结果为0
第五次 abcda 长度为1的前缀a 后缀a 他们是一样的，而长度更长的前缀后缀都不一样。 结果为1
第六次 abcdab 长度为2的前缀ab 后缀ab 他们是一样的，结果为2。
所以我们得到一个最长公共前缀后缀数组

a	b	c	d	a	b
0	0	0	0	1	2

next数组（对象是模式串，长度与模式串等长）
我们上面已经求得了最长公共前缀后缀数组，接下来我们把数组里的值都往后移动一格，第一位的值空出来了，我们填入-1，所获得的这个数组就是next数组了。如下：

a	b	c	d	a	b
-1	0	0	0	0	1

至于为什么要往后面移动一格，因为：
（当匹配到一个字符失配时，其实没必要考虑当前失配的字符。因为我们每次失配时，都是看的失配字符的上一位字符对应的最大长度值。如此引出了next 数组。
引自：https://www.cnblogs.com/zhangtianq/p/5839909.html）
这样我们遇到不匹配字符的时候，不用去看上一个字符的数字，直接查当前位置的next的值就好了。

KMP的next 数组告诉我们：当模式串中的某个字符跟文本串中的某个字符匹配失配时，模式串下一步应该跳到哪个位置。

匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值。 而 j 的新位置为失配字符对应的 next 值。

当然，实际使用中，用最长前缀后缀数组和用next数组都是一样的，他们都是一个东西，打起来代码不一样而已，推荐用next。

模板

#include 
using namespace std;
typedef long long ll;
int next[];
char s[];
char p[];
void GetNext(char* p,int next[])  
{  
    int pLen = strlen(p);  
    next[0] = -1;  
    int k = -1;  
    int j = 0;  
    while (j < pLen - 1) {  
        //p[k]表示前缀，p[j]表示后缀  
        if (k == -1 || p[j] == p[k])   
            next[++j] =++k;  
        else 
            k = next[k];  
    }  
}
//匹配算法
int KmpSearch(char* s, char* p)  
{  
    int i = 0;  
    int j = 0;  
    int sLen = strlen(s);  
    int pLen = strlen(p);  
    while (i < sLen && j < pLen)  
    {  
        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++      
        if (j == -1 || s[i] == p[j])  
            i++,j++; 
        else  
        {  
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]      
            //next[j]即为j所对应的next值        
            j = next[j];  
        }  
    }  
    if (j == pLen)  
        return i - j;  //返回了在文本串中的位置
    else  
        return -1;  
}

int  main()
{	
	
	return 0;
} 

---

exkmp算法

http://www.cnblogs.com/zjp-shadow/p/10139818.html#caioj-1461-exkmp 参考文章

给定字符串S , P ，其中S是母串，P是子串。
假设n = |S| , m = |P|，要求在线性时间里得到 extend[ ] 数组。
这里extend[ i ] 代表 S[ i …n ]和 P 的最长公共前缀(LCP)的长度。
也就是说，extend[ i ]代表 母串从i到n的这个后缀，与整个子串的最长公共前缀匹配长度(LCP)。
其中LCP是Longest Common Prefix

为什么说ex_kmp算法是对kmp的扩展呢？
我们可以发现，如果extend[i] = m，则子串P在母串S中出现过，且在S中出现的起始位置为i，这正是KMP所求的东西。所以ex_kmp算法是对kmp的扩展。

exkmp能解决的问题类型
很多字符串问题
1、在线性时间内求出母串的任意后缀 与 子串的最长公共前缀。
2、求一个字符串的最长回文子串。
3、一个字符串的最长重复子串。

时间复杂度
exkmp的时间复杂度为：O（m+n）
暴力匹配的时间复杂度为O（mn），会TLE。

算法过程
母串S，子串P。长度分别为n,m。
1、先求出nex[]数组，next[ i ] 表示子串 P 与 P_i–m LCP。这里用get_next()函数实现。
2、利用nex[]数组，线性的求出extend[]数组。这里用exkmp()函数实现。

exkmp的两个函数特别像，都是先初始化所求数组的第一位，初始化p0，然后线性跑一遍母串，求出数组每个位置的对应的值。
求每个值时分两种情况讨论：
一种是能直接得到的
一种是还要继续匹配下去求得的（继续匹配内部又分为是否要从头开始匹配）。

算法过程图解

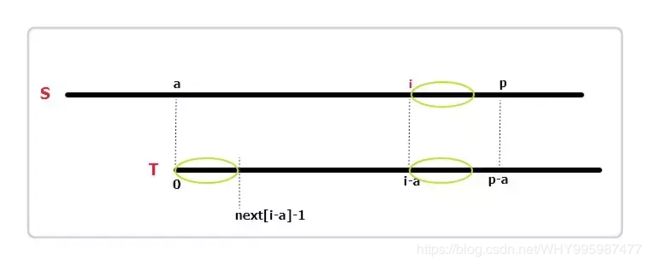
 （1）如上图，假设当前遍历到S串位置i，即extend[0]…extend[i-1]这i个位置的值已经计算得到。算法在遍历过程中记录了匹配成功的字符的最远位置p，及这次匹配的起始位置a。相较于字符串T得出，S[a]…S[p]等于T[0]…T[p-a]。
 
  再定义一个辅助数组int next[]，其中next[i]含义为：T[i]…T[m-1]与T的最长公共前缀长度，m为串T的长度。

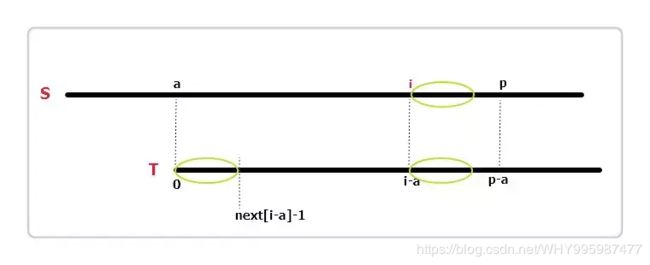
（2）椭圆的长度为next[i-a]，对比S和T，很容易发现，三个椭圆完全相同。此时i+next[i-a]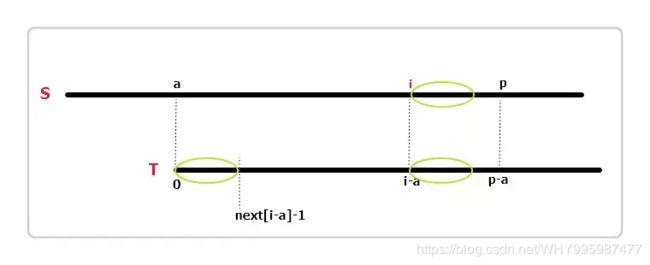
 （3） 如果i+next[i-a]>=p呢？仔细观察上图，可以发现i+next[i-a]是不可能大于p的，如果可以大于p，那么以a为起始位置的最远匹配位置就不是p了，而是更加后面的位置，因此i+next[i-a]只可以小于等于p。
这是小于的情况，接下来是等于的情况。
如果三个椭圆都是完全相同的，此时我们可以直接从S[p]与T[next[i-a]-1]开始往后匹配，加快了速度。

（4）最后，就是求解next数组。
我们再来看下next与extend的定义：
next[i]： T[i]…T[m-1]与T的最长公共前缀长度；
extend[i]： S[i]…S[n-1]与T的最长公共前缀的长度。

所以求解next的过程就是T自己和自己的一个匹配过程。
例题
19杭电暑假多校 第5场 第六题string matching

EXKMP模板

const int MAXN=100000;
int next[MAXN];
int extend[MAXN];
void getNext(char *str)
{
    int len=strlen(str),p0,i=0,j;
    next[0]=len;//初始化next［０］
    while(str[i]==str[i+1]&&i+1<len) i++;
    next[1]=i;
    p0=1;//初始化p0
    for(i=2;i<len;i++)
    {
        if(next[i-p0]+i<next[p0]+p0) next[i]=next[i-p0];//第一种情况，可以直接得到next[i]的值
        else//第二种情况，要继续匹配才能得到next[i]的值  
        {
            j=next[p0]+p0-i;//如果i>po+next[po],则要从头开始匹配
            if(j<0) j=0;
            while(i+j<len&&str[i+j]==str[j]) j++;//计算next[i]
            next[i]=j;
            p0=i;
        }
    }
}
void exkmp(char *str,char *p)//计算extend数组 
{
    int i=0,j,p0,slen=strlen(str),plen=strlen(p);
    getNext(p);//计算p的next数组
    while(i<slen&&i<plen&&str[i]==p[i]) i++;//计算ex[0]  
    extend[0]=i;
    p0=0;//初始化po的位置  
    for(i=1;i<slen;i++)
    {
        if(next[i-p0]+i<extend[p0]+p0) extend[i]=next[i-p0];//第一种情况，直接可以得到ex[i]的值
        else //第二种情况，要继续匹配才能得到ex[i]的值  
        {
            j=extend[p0]+p0-i;
            if(j<0) j=0;//如果i>ex[po]+po则要从头开始匹配
            while(i+j<slen&&j<plen&&str[i+j]==p[j]) j++;//计算ex[i]
            extend[i]=j;
            p0=i;//更新po的位置  
        }
    }
}

BM算法

后缀匹配，从后往前跑。有坏字符。
还没学。
https://www.cnblogs.com/wxgblogs/p/5701101.html

sunday算法

以下sunday算法部分，转自
https://www.cnblogs.com/zhangtianq/p/5839909.html
侵删

KMP算法和BM算法，这两个算法在最坏情况下均具有线性的查找时间。但实际上，KMP算法并不比最简单的c库函数strstr()快多少，而BM算法虽然通常比KMP算法快，但BM算法也还不是现有字符串查找算法中最快的算法，本文最后再介绍一种比BM算法更快的查找算法即Sunday算法。

Sunday算法由Daniel M.Sunday在1990年提出，它的思想跟BM算法很相似，只不过Sunday算法是从前往后匹配，在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。
如果该字符没有在模式串中出现则直接跳过，即移动位数 = 匹配串长度 + 1；
否则，其移动位数 = 模式串中最右端的该字符到末尾的距离+1。
下面举个例子说明下Sunday算法。假定现在要在文本串"substring searching algorithm"中查找模式串"search"。

1. 刚开始时，把模式串与文本串左边对齐：
   substring searching algorithm
   search
   ^
2. 结果发现在第2个字符处发现不匹配，不匹配时关注文本串中参加匹配的最末位字符的下一位字符，即标粗的字符 i，因为模式串search中并不存在i，所以模式串直接跳过一大片，向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7，从 i 之后的那个字符（即字符n）开始下一步的匹配，如下图：

substring searching algorithm
　　　search
　　　^

3. 结果第一个字符就不匹配，再看文本串中参加匹配的最末位字符的下一位字符，是’r’，它出现在模式串中的倒数第3位，于是把模式串向右移动3位（r 到模式串末尾的距离 + 1 = 2 + 1 =3），使两个’r’对齐，如下：
   substring searching algorithm
   　　　　 search
   　　　　　　 ^
4. 匹配成功。
   回顾整个过程，我们只移动了两次模式串就找到了匹配位置，缘于Sunday算法每一步的移动量都比较大，效率很高。完。