字符串匹配：字符串hash，后缀数组，高度数组，AC自动机，KMP

参考博客：
https://www.cnblogs.com/jinkun113/p/4743694.html
https://mp.weixin.qq.com/s?src=11×tamp=1586784093&ver=2276&signature=fIW2gkvXML6aFFC8i0vzAaI4AcLhTZDETqQhNeAt4UvGMqmW5X3FlLEGbp5xbEKsJxl-juGPgj1vqk6-V8WHau0QZZzuaOabSvlTj4f8R1v6sVSwpBVeiVe6xW4Oc5Hc&new=1

一、字符串hash

字符串hash+二分入门题
二维字符串哈希
寻找字符串s中字符串t出现的位置或次数的问题属于字符串匹配问题。我们在接下来的讨论中假设s的长度为n,T的长度为m。 最朴素的想法是，枚举所有起始位置，再直接检查是否匹配，复杂度为$O(mn)$的算法。还有几个更为高效的算法。而在此我们只介绍实现起来较为容易，而在一些稍作变化的问题中同样适用，并且可以简单地推广到二维情况的哈希算法(散列算法)

将哈希算法用于字符算匹配的原理非常简单。对于每个起始位置，我们不是$O(m)$地直接比较字符串是否匹配，而是$O(l)$地比较长度为$m$的字符串子串的哈希值与$T$的哈希值是否相等。虽然即使哈希值相等字符串也未必相等，但如果哈希值是随机分布的话，不同的字符串哈希值相等的概率是很低的，可以当作这种情况不会发生。

但是，如果我们采用$O(m)$的算法计算长度为m的字符串子串的哈希值的话，那复杂度还是$O(mn)$，这里我们要使用一个叫做滚动哈希的优化技巧。选取两个合适的互素常数$b$和$h(l<b<h)$叫,假设字符串$C=c_1{c}_2...c_m$，定义哈希函数

$$H(C)=(c_1{b}^{m-1}+c_2{b}^{m-2}+...+c_m{b}^0)\%h$$

其中$b$是基数，相当于把字符串看作$b$进制数。这样，字符串$S=s_1{s}_2...s_n$从位置$k+1$开始长度为$m$的字符串字串$S[k+1...k+m]$的哈希值，就可以利用从位置k开始的字符串子串$S[k...k+m-1]$的哈希值直接计算。

$$H(S[k+1...k+m])=(H(S[k...k+m-1])\ast b-s_k{b}^m+s_{k+m})$$

于是，只要不断这样计算开始位置右移一位后的字符串子串的哈希值，就可以在$O(n)$时间内得到所有位置对应的哈希值，从而可以在$O(m+n)$时间内完成字符串匹配。在实现时，可以用64位无符号整数计算哈希值，并取$h$等于$2^{64}$通过自然溢出省去求模运算。而$b$一般取31，131

当然，不光是右移一位，对于左移一位、左端或右端加长一位或是缩短一位的情况，也能够进行类似处理。譬如说，假设要求S的后缀和T的前缀相等的最大长度，也可以利用滚动哈希在$O(n+m)$的时间内高效地求得。

模板：

for (int j = 0; j < Q; j++)t1 *= b1;//计算 t1^Q
ull e = 0;
for (int j = 0; j < Q; j++) e = e * b1 + [j];

for (int j = 0; j + Q <= m; j++) {//等于m只是为了给tmp赋值
	tmp[j] = e;
	if (j + Q < m)e = e * b1 - t1 * a[j] + [j + Q];
}

二、后缀数组

一串三分求最小
字符串后缀（Suffix) 指的是从字符串的某个位置开始到其末尾的字符串子串。我们认为原串和空串也是后缀。反之，从字符串开头到某个位置的字符串子串则称为前缀。

后缀数组（ Suffix Array )指的是将某个字符串的所有后缀按字典序排序后得到的数组。不过数组中并不需要直接保存所有的后缀字符串，只要记录对应的起始位置就好了。下文中，我们用$S[i..]$来表示字符串$S$从位置$i$开始的后缀。

1:后缀数组的计算

首先假定一个字符串BANANA，在后面添加一个非字母字符“$”，代表一个没出现过的标识字符，然后把它的所有后缀——
$$BANANA\$,ANANA\$,NANA\$,ANA\$,NA\$,A\$$$

插入到一棵Trie中。由于标识字符的存在，字符串每一个后缀都与一个叶节点一一对应。如图所示：

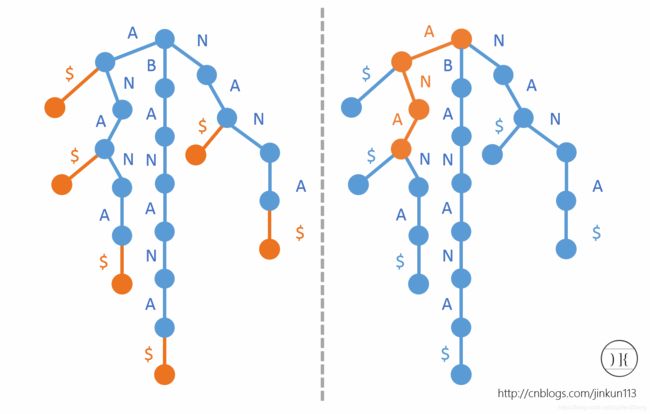
我们发现，有了后缀Trie之后，可以O(m)查找一个单词，如右侧。

在实际应用中，会把后缀Trie中没有分支的链合并在一起，得到所谓的后缀树，但是由于后缀树的构造算法复杂难懂，且容易写错，所以在竞赛中很少使用，所以暂时不去研究了。相比之下，后缀数组是必备武器，时间效率高，代码简单，而且不易写错。

在绘制后缀Trie的时候，我们将字典序小的字母排在左边。由于叶节点和后缀一一对应，我们现在在每一个叶节点上标上该后缀的首字母在原字符串中的位置，如图：

　　将所有下标连在一起，构建出来的，就是所谓的后缀数组了。BANANA的后缀数组为sa[] = {5, 3, 1, 0, 4, 2}，举个例子，其中sa[1] = 3表示第3 + 1 = 4个字母开头的后缀即"ANA"在所有后缀中字典序排名为1。这样的话，我们就可以直接通过一次快速排序O(n log n)得到了。但是，在比较任意两个后缀时，又需要O(n)，故这是O(n^2 log n)，根本扛不住。

下面介绍Manber和Myers发明的倍增算法，时间复杂度O(n log n)（不采用基数排序的话就是O(n log^2 n)）。

首先对于所有单个字符排序（也可以理解成对于每一个后缀的第1个字符排序，这样后面的步骤更易衔接），如图：

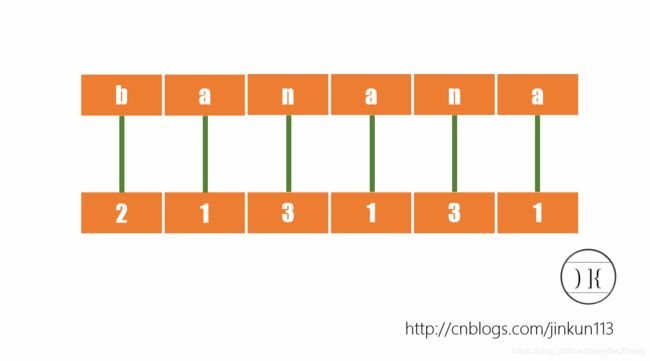
对于每个字母，我们根据字典序给予其一个名次，则a->1，b->2，n->3。

而接下来，我们再给所有后缀的前两个字符排序（之前就是前一个），将相邻二元组合并，再次根据字典序给予一个名次，如图：

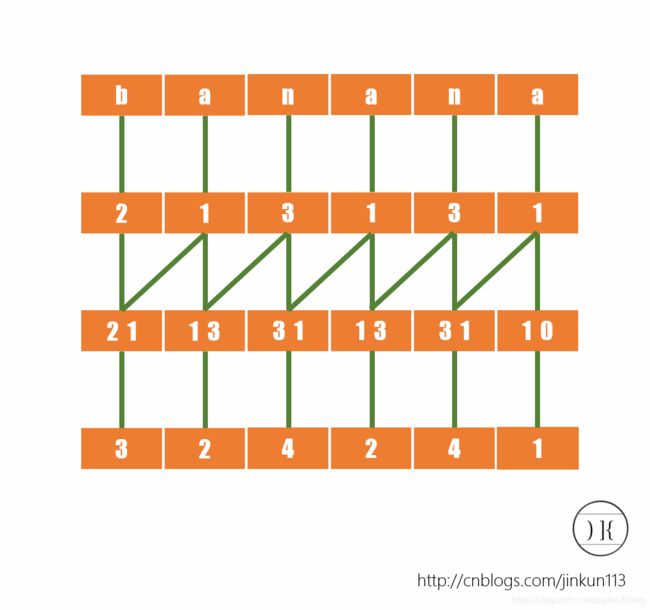
　　而我们现在得到了所有后缀的前2个字符的排名，注意这种方法是倍增思想，接下来要求的就是所有后缀的前4个字符的名次，因为可知对于后缀x的前4个字符是由后缀x的前2个字符和后缀x+2的前2个字符组成的，方法同上。如图：

我们也可以注意到，当我们试图再去把所有后缀的前8个字符排一遍序的时候会发现，并没有任何含义。首先，这个字符串的长度没有达到8，其次所有名词已经两两不同，已经达到了我们的目的。所以我们可以分析出，这个过程的时间复杂度稳定为O(log n)。

得到了序列a[]={4,3,6,2,5,1}，a[i]表示后缀i的名次。而后我们可以得到后缀数组了：sa[]={5,3,1,0,4,2}。（你要问我怎么得到的嘛？）

相信只要理解字符串的比较法则(跟实数差不多)，理解起来并不难。#还有一个细节就是怎么把这些两位数排序？这种位数少的数进行排序毫无疑问的要用一个复杂度为长度*排序数的个数的优美算法——基数排序(对于两位数的数复杂度就是O(Len)的)。

基数排序原理 ： 把数字依次按照由低位到高位依次排序，排序时只看当前位。对于每一位排序时，因为上一位已经是有序的，所以这一位相等或符合大小条件时就不用交换位置，如果不符合大小条件就交换，实现可以用”桶”来做。(叙说起来比较奇怪，看完下面的代码应该更好理解，也可以上网查有关资料)

2：基于后缀数组的字符串匹配

后缀数组最基本的应用便是字符串匹配了。假设已经计算好了字符串S的后缀数组，现在要求字符串m字符串s中出现的位置，只要通过二分搜索就可以在$O(|T|\log |S|)$时间完成，当$|S|$比较大时,该算法也可以保持高效，所以需要对同样的字符串做多次匹配时，该算法更有优势。

3：模板：计算与字符匹配

//Rank[i] : 第i位开始的后缀在所有后缀中的排名  
//sa[i]：排名为i的后缀是从第几位开始的
//tmp:临时数组，帮助计算RANK
int Rank[MAX], sa[MAX], tmp[MAX];
//待处理字符串长度为n
int n, k; 

//比较（Rank[i], Rank[i + k])和（Rank[j], Rank[j + k])
bool cmp_sa(int i, int j) {
	// i,j是两个需要比较的k位字符的高位
	if (Rank[i] != Rank[j]) return Rank[i] < Rank[j];
	else {//i+k,j+k是个位元素   注意这里小于等于
		int ri = i + k <= n ? Rank[i + k] : -1;//超出长度限制的优先级最高
		int rj = j + k <= n ? Rank[j + k] : -1;	
		return ri < rj;
	}
}

// 计算字符串s的后缀数组
void build(string s) {
	n = s.length();

	// 初始长度为1, Rank直接取字符的编码  等于n代表空字符串
	for (int i = 0; i <= n; i++) {
		sa[i] = i;
		Rank[i] = i < n ? s[i] : -1;
	}

	// 利用对长度为k的排序的结果对长度为2k的排序
	for (k = 1; k <= n; k *= 2) {
		sort(sa, sa + 1 + n, cmp_sa);

		// 先在tmp中临时存储新计算的rank, 再转存回rank中
		// sa[0]取出排名0的后缀开始位数  tmp[sa[0]]将该位开始的后缀的rank存储为0
		tmp[sa[0]] = 0;
		//核心语句
		for (int i = 1; i <= n; i++) {
			//sa[i]取出排名为i的后缀开始位数
			//和排名为i-1的后缀sa[i-1]进行比较
			//如果在此时的k的情况下 二者相等则rank相等
			//由于sa上一轮已经排序过了 sa[i]不可能比sa[i-1]更小 因此不相等就rank+1
			//注意相邻的两个rank有什么规律呢？为什么相邻rank比较就可以呢？--仔细看表
			tmp[sa[i]] = tmp[sa[i - 1]] + (cmp_sa(sa[i - 1], sa[i]) ? 1 : 0);
		}
		for (int i = 0; i <= n; i++)Rank[i] = tmp[i];
	}
}

bool contain(string s, string t) {
	int a = 0, b = s.length(), len = t.length();
	while (b - a > 1) {
		int mid = (a + b) >> 1;
		// 比较s从位置sa[c]开始长度为|t|的子串与t
		// sc[c]是排名为c的字符串开始位置，可以看到二分查找的是排名
		//compare(sa[mid], len, t) 从sa[mid]位置开始连续的len个元素与t相比较 内置函数
		//字典序小就需要一个排名靠后的，否则需要一个排名靠前的
		if (s.compare(sa[mid], len, t) < 0)a = mid;
		else b = mid;
	}
	//b不一定就是正确答案，有可能是走投无路
	return s.compare(sa[b], len, t) == 0;
}

三、高度数组（LCP， Longest Common Prefix Array)

高度数组同样是一个非常重要的知识点，所谓高度数组，指的是由后缀数组中相邻两个后缀的最长公共前缀( LCP， Longest Common Prefix Array )的长度组成的数组（即相邻rank的最长公共前缀长度）。记后缀数组为sa，高度数组为lcp，则有后缀$S[sa[i]...]$与$S[sa[i+1]...]$的最长公共前缀的长度为$lcp[i]$。我们可以在$O(n)$时间内高效地求得高度数组，有了高度数组，后缀数组将成为一个更加有力的工具。高度数组的计算虽然简单，但非常巧妙，使用了类似尺取法的技巧。记$rank[i]$为位置i开始的后缀在后缀数组中的顺序，即有$rank[sa[i]]=i$，和上文一样，这两个是互逆的运算。

我们从位置0的后缀开始，从前往后依次计算后缀$S[i...]$和后缀$S[sa[rank[i]-1]...]$(即后缀数组中的前一个后缀）的最长公共前缀的长度。这里可能有点难以理解，$rank[i]-1$即比$rank[i]$低一个的等级，$sa[ranl[i]-1]$取出这个等级的开始元素，$S[sa[rank[i]-1]...]$取出整个串。也就是所说的，前缀数组中的前一个后缀。

~未完待续

四、KMP

详细的KMP教程+模板

五、AC自动机

AC自动机的跳转移边优化+简洁模板