HashMap源码解析(2)—— hash & (n - 1)
本篇详细解析下(JDK1.8) HashMap 中使用的哈希函数 —— hash & (n - 1)。
如果对哈希函数这个概念不理解,可以参看之前的博客——哈希函数 上、哈希函数 下
哈希函数用一句话通俗的讲,就是 将 key 值转化为数组下标,结合下图
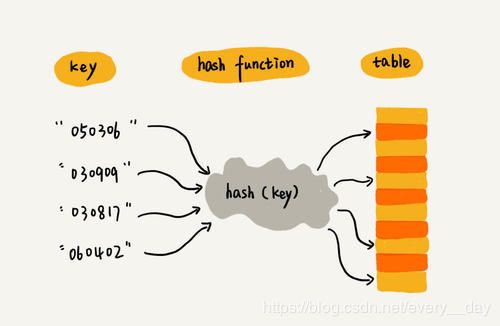
比如数组长度是15, 给一个最简单的哈希函数,key的hashcode,对15取余。
String key = "050306";
int code = key.hashCode(); // code:1424626382
int len = 15;
int index = code % len; // index:2
这里不考虑函数性能,哈希冲突等等情况,只是给一个哈希函数的概念。
如果以上的都理解了,现在切入正题,HashMap中采用的哈希函数。
hash & (n - 1)
标题的式子n 是哈希桶的个数(可以近似理解为上个例子中的数组长度)
式子中的hash 是下面这段代码——hash(key),计算出的一个int数值。
hash & (n - 1) 近似理解为计算出的数组下标。
- hash(key)
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
举个例子
String key = "test";
int code = key.hashCode(); // 3556498
int code_16 = code >>> 16; // 54
int hash = code ^ code_16; // 3556516
-----------------二进制如下-----------------
code: 11 0110 0100 0100 1001 0010
code_16: 00 0000 0000 0000 0011 0110
hash: 11 0110 0100 0100 1010 0100
据说这么计算可以减少哈希冲突,为什么,说实话我也不知道。
- n——哈希桶
哈希函数中,n 永远是2的次方,即 2, 4,8,16,32,64……
在HashMap中是如何保证这一点的,这个之后的文章再详细说,不是今天的重点。
今天先记住 n 是 2 的次方,等会儿会用到这个。
- hash & (n - 1)
开始我一直不理解,为什么下标计算可以用这个公式,查了资料,想了好久,终于理解了。
便于理解,我们直接赋值来说明, hash就用前面例子中计算出来的3556516,n 取8即 23
hash & (n - 1) = hash % n,即 3556516 & 7 = 3556516 % 8
放心不理解是正常的哈,说他第一眼看到这个,就明白啥意思,那一定是瞎掰。哈哈
今天重点:为什么 hash & (n - 1) = hash % n ??
3556516 转化成二进制是 11 0110 0100 0100 1010 0100
3556516 & 7 结果是,二进制的后三位
3556516 % 8结果也是,二进制的后三位
先说说 3556516 & 7 =二进制的后三位
11 0110 0100 0100 1010 0100 ---- 3556516的二进制
00 0000 0000 0000 0000 0111 ---- 7的二进制
00 0000 0000 0000 0000 0100 ---- 3556516 & 7
7=23-1,二进制,最后三位是1,其余全部是0(前面说过,n是2的次方,n-1的二进制一定满足,后面全是1,前面全是0)
& 运算的性质,两者同是1得1,否则得0,
那细想下,3556516 & 7,得到的不就是3556516的二进制的后三位么。这个不懂仔细想想,画画。
至此,3556516 & 7 结果是,二进制的后三位这个就讲完了,
即 3556516 & 7= 4(也就是3556516 二进制的最后三位100)
再说说3556516 % 8=二进制的后三位
先看这两个式子
20 / 8 = (16 + 4) / 8 = 2 余数 4
20 % 8 = (16 + 4)% 8 = 4
这两个式子,相信大家应该能看懂,20 % 8,把20分成两部分,一部分能整除8,另一部分小于8,肯定就是余数了。
20的二进制 = 10100
二进制转化十进行是这么计算的
10100 = 1 * 24 + 0 * 23 + 1 * 22 + 0 * 21 + 0 * 20 = (1 * 24 + 0 * 23) + (1 * 22 + 0 * 21 + 0 * 20)
20 % 8 = (16 + 4)% 8 = 4 如果这个你懂了的话,上面那上二进制的式子中,第一个括号里的肯定能被8整除,第二个括号里的就是余数。
即:20 % 8 = 二进制10100的后三位。3556516 % 8=二进制的后三位是一个道理。
好了,费了这么大的劲儿,终于解释了
hash & (n - 1) = hash % n
为什么用hash & (n - 1) ,而不是用 hash % n
HashMap 中的哈希函数 hash & (n - 1) 跟取余运算 hash % n 结果是一致的。那它为什么不直接用取余运算呢?
答案两个字——性能。
我写了个不太严谨的代码,比较两者速度的差异
public static void main(String[] args) throws Exception {
int count = 200000000;
int len = 8;
int hash = 3556516;
int result = hash % 8;
long time_1 = System.nanoTime();
for(int i = 0; i < count; i++){
result = hash % len;
}
long time_2 = System.nanoTime();
for(int i = 0; i < count; i++){
result = hash & (len - 1);
}
long time_3 = System.nanoTime();
System.out.println("循环次数:" + (count));
System.out.println("hash % 8 运算消耗 纳秒数" + (time_2 - time_1));
System.out.println("hash & 7 运算消耗 纳秒数" + (time_3 - time_2));
}
----------------------------------------------------------
循环次数:200000000
hash % 8 运算消耗 纳秒数6453653
hash & 7 运算消耗 纳秒数1399112
运行了两亿次,速度确实有差别,两亿次,都是毫秒级别完成,差几个毫秒吧。就算它两亿次,快了10毫秒,平均一次,快了0.05纳秒。
我还特意查了一下,光在真空中一纳秒仅传播0.3米。
如果我站在镜子前面1.5米,眨了眨眼睛,理论上,镜子里动作,比现实中的动作慢了10纳秒。
那0.05纳生秒是什么概念,自己体会吧。
我不是在吐槽性能提升的太少,想想,极端情况下,如果hashMap中存了几千万的数据。
碰巧,某次插入数据时,引发扩容了,那就要重新计算下标值,即进行几千万次的hash & (n - 1)运算。
微乎其微的性能提升,累积起来,性能提升还是可观的。
毕竟HashMap太基础,使用的频次太高了,任何一点点的性能提升都不容小觑。
但是,如果是平常码代码,一个hash % n运算,偏偏要写一个hash & (n - 1),那就是装,理解起来费劲,代码别人看不懂,还怎么维护。
我丫丫的就是不相信,0.05纳秒级别的性能提升,在你的系统里能感知出来。