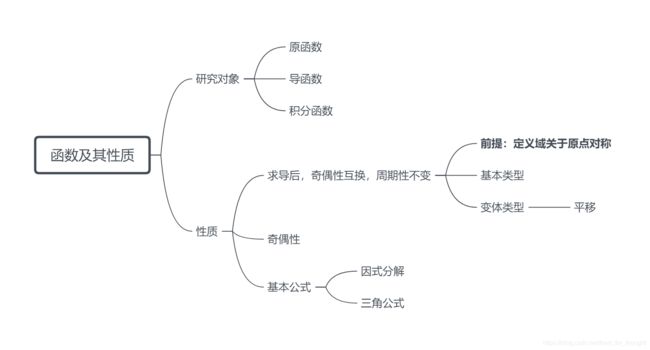
【数学】函数及其性质(宇哥笔记)
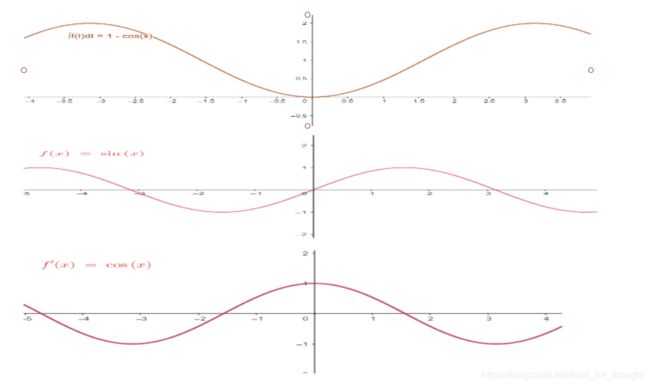
微积分的研究对象为函数的“祖孙三代”,爷爷是积分函数,爸爸是原函数,儿子是导函数,积分函数可以求导得原函数,导函数可以求积分得到原函数,以 sinx 为原函数,可得以下图示。
性质
求导后:奇偶性互换,周期性不变
[ 例 ] : f ( x ) 二 阶 可 导 , T = 2 , 奇 函 数 , f ( 1 2 ) > 0 , f ′ ( x ) > 0 , 比 较 f ( − 1 2 ) , f ′ ( 2 3 ) , f ′ ′ ( 0 ) 的 大 小 ∵ 该 函 数 为 奇 函 数 ∴ f ( − x ) = − f ( x ) → f ( − 1 2 ) = − f ( 1 2 ) < 0 ∵ f ( x ) : T = 2 ∴ f ′ ( x ) : T = 2 且 f ′ ( x ) 为 偶 函 数 ∴ f ′ ( 2 3 ) = f ′ ( 2 3 − 2 ) = f ′ ( − 1 2 ) = f ′ ( 1 2 ) > 0 ∴ f ′ ′ ( x ) 为 奇 函 数 即 : f ′ ′ ( 0 ) = 0 得 f ( − 1 2 ) < f ′ ′ ( 0 ) < f ′ ( 1 2 ) [例]:f(x)二阶可导,T=2,奇函数,f(\frac12)>0,f'(x)>0,比较f(-\frac12),f'(\frac23),f''(0)的大小\\ \because该函数为奇函数\therefore f(-x)=-f(x)\rightarrow f(-\frac12)=-f(\frac12)<0\\ \because f(x):T=2 \therefore f'(x):T=2且f'(x)为偶函数 \\ \therefore f'(\frac23)=f'(\frac23-2)=f'(-\frac12)=f'(\frac12)>0\\ \therefore f''(x)为奇函数\quad 即:f''(0)=0\\得f(-\frac12)<f''(0)<f'(\frac12) [例]:f(x)二阶可导,T=2,奇函数,f(21)>0,f′(x)>0,比较f(−21),f′(32),f′′(0)的大小∵该函数为奇函数∴f(−x)=−f(x)→f(−21)=−f(21)<0∵f(x):T=2∴f′(x):T=2且f′(x)为偶函数∴f′(32)=f′(32−2)=f′(−21)=f′(21)>0∴f′′(x)为奇函数即:f′′(0)=0得f(−21)<f′′(0)<f′(21)
1.前提:定义域关于原点对称
2.基本类型:
1. f ( x ) + f ( − x ) 为 偶 函 数 , 如 e x + e − x 2 ; ( 1 + x ) 2 3 + ( 1 − x ) 2 3 1.f(x)+f(-x)为偶函数,如\frac{e^x+e^{-x}}{2};\sqrt[3]{(1+x)^2}+\sqrt[3]{(1-x)^2} 1.f(x)+f(−x)为偶函数,如2ex+e−x;3(1+x)2+3(1−x)2
2. f ( x ) − f ( − x ) 为 奇 函 数 , 如 e x − e − x 2 ; ln 1 + x 1 − x 2.f(x)-f(-x)为奇函数,如\frac{e^x-e^{-x}}{2};\ln\frac{1+x}{1-x} 2.f(x)−f(−x)为奇函数,如2ex−e−x;ln1−x1+x
3. f [ ψ ( x ) ] 为 复 合 函 数 奇 [ 偶 ] = 偶 : s i n x 2 偶 [ 奇 ] = 偶 : c o s ( s i n x ) ; ∣ s i n x ∣ 奇 [ 奇 ] = 奇 : s i n 1 x ; t a n x 3 偶 [ 偶 ] = 偶 : c o s ∣ x ∣ ; ∣ c o s x ∣ 非 [ 偶 ] = 偶 : e x 2 ; ln ∣ x ∣ 3.f[\psi(x)]为复合函数\\奇[偶]=偶:sinx^2\\偶[奇]=偶:cos(sinx);\mid sinx\mid \\ 奇[奇]=奇:sin\frac1x;\sqrt[3]{tanx} \\ 偶[偶]=偶:cos\mid x \mid ;\mid cosx \mid \\非[偶]=偶:e^{x^2};\ln\mid x\mid 3.f[ψ(x)]为复合函数奇[偶]=偶:sinx2偶[奇]=偶:cos(sinx);∣sinx∣奇[奇]=奇:sinx1;3tanx偶[偶]=偶:cos∣x∣;∣cosx∣非[偶]=偶:ex2;ln∣x∣
4. 一 个 特 殊 函 数 : ln ( x + 1 + x 2 ) 为 奇 函 数 4.一个特殊函数:\ln(x+\sqrt{1+x^2})为奇函数 4.一个特殊函数:ln(x+1+x2)为奇函数
!
5. 求 导 后 奇 偶 性 互 换 6. 以 0 为 下 限 , 求 积 分 后 奇 偶 性 互 换 , 如 f ( x ) 为 奇 函 数 , 则 ∫ 0 x f ( t ) d t 为 偶 函 数 7. ( 题 源 ) f ( x ) 连 续 , ∀ x , y , 使 f ( x + y ) = f ( x ) + f ( y ) → f ( x ) 为 奇 函 数 证 明 : 取 y = 0 , f ( x ) = f ( x ) + f ( 0 ) = f ( 0 ) = 0 ; 取 y = − x , f ( 0 ) = f ( x ) + f ( − x ) → f ( x ) = − f ( − x ) [ 例 ] ∫ − 1 1 ln ( x + 1 + x 2 ) e − x 2 d x = 0 , 前 者 是 4 的 奇 函 数 , 后 者 为 偶 函 数 , 得 奇 函 数 ∫ − 1 1 ( ∫ 0 x e − t 2 d t ) x 2 d x = 0 , 前 者 为 奇 函 数 , 后 者 为 偶 函 数 , 得 奇 函 数 以 7 为 前 置 条 件 , ∫ − 1 1 ( x 2 + 1 ) f ( x ) d x = 0 , 前 者 为 偶 函 数 , 后 者 为 奇 函 数 , 得 奇 函 数 5.求导后奇偶性互换\\ 6.以0为下限,求积分后奇偶性互换,如f(x)为奇函数,则\int_0^xf(t)dt为偶函数\\ 7.(题源)f(x)连续,\forall x,y,使f(x+y)=f(x)+f(y)\rightarrow f(x)为奇函数\\ 证明:取y=0,f(x)=f(x)+f(0)=f(0)=0;取y=-x,f(0)=f(x)+f(-x)\rightarrow f(x)=-f(-x)\\ [例]\int_{-1}^1\ln(x+\sqrt{1+x^2})e^{-x^2}dx=0,前者是4的奇函数,后者为偶函数,得奇函数\\ \int_{-1}^1(\int_0^xe^{-t^2}dt)x^2dx=0,前者为奇函数,后者为偶函数,得奇函数\\ 以7为前置条件,\int_{-1}^1(x^2+1)f(x)dx=0,前者为偶函数,后者为奇函数,得奇函数 5.求导后奇偶性互换6.以0为下限,求积分后奇偶性互换,如f(x)为奇函数,则∫0xf(t)dt为偶函数7.(题源)f(x)连续,∀x,y,使f(x+y)=f(x)+f(y)→f(x)为奇函数证明:取y=0,f(x)=f(x)+f(0)=f(0)=0;取y=−x,f(0)=f(x)+f(−x)→f(x)=−f(−x)[例]∫−11ln(x+1+x2)e−x2dx=0,前者是4的奇函数,后者为偶函数,得奇函数∫−11(∫0xe−t2dt)x2dx=0,前者为奇函数,后者为偶函数,得奇函数以7为前置条件,∫−11(x2+1)f(x)dx=0,前者为偶函数,后者为奇函数,得奇函数
3.变体类型(平移):
1. f ( x ) 为 偶 函 数 → 关 于 y 轴 对 称 , 即 f ( 0 + x ) = f ( 0 − x ) ( 平 移 ) 得 f ( x ) 关 于 x = T 对 称 , 即 f ( T + x ) = f ( T − x ) [ 例 ] f ( x ) 为 正 值 且 连 续 , ∫ − ∞ + ∞ f ( x ) d x = 1 , 又 f ( 1 + x ) = f ( 1 − x ) , 且 ∫ 0 2 f ( x ) d x = 0.6 , 则 ∫ − ∞ 0 f ( x ) d x = 0.2 2. f ( x ) 为 奇 函 数 → 关 于 ( 0 , 0 ) 对 称 , ( 平 移 ) → 关 于 ( x 0 , 0 ) 对 称 , 如 x 3 → ( x − 1 ) 3 [ 例 ] ∫ − 1 1 x 3 d x = 0 ; ∫ 0 2 ( x − 1 ) 3 d x = 0 ; ∫ 0 4 ( x − 2 ) d x = 0 1.f(x)为偶函数\rightarrow 关于y轴对称,即f(0+x)=f(0-x) (平移)得f(x)关于x=T对称,即f(T+x)=f(T-x)\\ [例]f(x)为正值且连续,\int_{-\infty}^{+\infty}f(x)dx=1,又f(1+x)=f(1-x),且\int_0^2f(x)dx=0.6,则\int_{-\infty}^0f(x)dx=0.2\\ 2.f(x)为奇函数\rightarrow关于(0,0)对称,(平移)\rightarrow关于(x_0,0)对称,如x^3\rightarrow (x-1)^3\\ [例]\int_{-1}^1x^3dx=0;\int_0^2(x-1)^3dx=0;\int_0^4(x-2)dx=0 1.f(x)为偶函数→关于y轴对称,即f(0+x)=f(0−x)(平移)得f(x)关于x=T对称,即f(T+x)=f(T−x)[例]f(x)为正值且连续,∫−∞+∞f(x)dx=1,又f(1+x)=f(1−x),且∫02f(x)dx=0.6,则∫−∞0f(x)dx=0.22.f(x)为奇函数→关于(0,0)对称,(平移)→关于(x0,0)对称,如x3→(x−1)3[例]∫−11x3dx=0;∫02(x−1)3dx=0;∫04(x−2)dx=0
奇偶性
偶 函 数 ⋅ 偶 函 数 = 偶 函 数 奇 函 数 ⋅ 奇 函 数 = 奇 函 数 奇 函 数 ⋅ 偶 函 数 = 奇 函 数 偶函数\cdot偶函数=偶函数\qquad奇函数\cdot奇函数=奇函数\qquad奇函数\cdot偶函数=奇函数 偶函数⋅偶函数=偶函数奇函数⋅奇函数=奇函数奇函数⋅偶函数=奇函数
基本公式
因 式 分 解 公 式 ( a + b ) 2 = a 2 + 2 a b + b 2 ( a − b ) 2 = a 2 − 2 a b + b 2 ( a + b ) 3 = a 3 + b 3 + 3 a 2 b + 3 a b 2 ( a − b ) 3 = a 3 − b 3 − 3 a 2 b + 3 a b 2 a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a 2 − b 2 = ( a + b ) ( a − b ) a n − b n = ( a − b ) ( a n − 1 − a n − 2 b + ⋯ + a b n − 2 + b n − 1 ) 因式分解公式\\ (a+b)^2=a^2+2ab+b^2\qquad(a-b)^2=a^2-2ab+b^2\\ (a+b)^3=a^3+b^3+3a^2b+3ab^2\qquad(a-b)^3=a^3-b^3-3a^2b+3ab^2\\ a^3+b^3=(a+b)(a^2-ab+b^2)\qquad a^3-b^3=(a-b)(a^2+ab+b^2)\\ a^2-b^2=(a+b)(a-b)\qquad a^n-b^n=(a-b)(a^{n-1}-a^{n-2}b+\cdots+ab^{n-2}+b^{n-1}) 因式分解公式(a+b)2=a2+2ab+b2(a−b)2=a2−2ab+b2(a+b)3=a3+b3+3a2b+3ab2(a−b)3=a3−b3−3a2b+3ab2a3+b3=(a+b)(a2−ab+b2)a3−b3=(a−b)(a2+ab+b2)a2−b2=(a+b)(a−b)an−bn=(a−b)(an−1−an−2b+⋯+abn−2+bn−1)
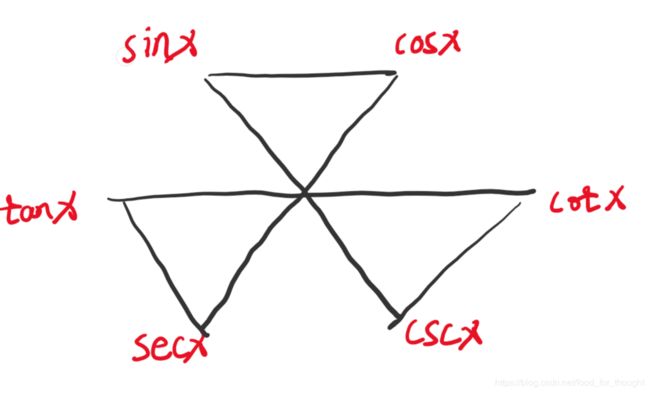
s i n 2 x + c o s 2 x = 1 t a n 2 x + 1 = s e c 2 x 1 + c o t 2 x = c s c 2 x s i n x ⋅ c s c x = 1 c o s x ⋅ s e c x = 1 t a n x ⋅ c o t x = 1 sin^2x+cos^2x=1\qquad tan^2x+1=sec^2x\qquad1+cot^2x=csc^2x\\ sinx\cdot cscx=1\qquad cosx\cdot secx=1\qquad tanx\cdot cotx=1 sin2x+cos2x=1tan2x+1=sec2x1+cot2x=csc2xsinx⋅cscx=1cosx⋅secx=1tanx⋅cotx=1