对深度学习反卷积网络的理解

在计算机视觉领域，很多模型都用到了反卷积，但是有一点让我很迷惑：有的论文代码中，反卷积是直接调用ConvTranspose2d()函数，而有的是先upsample(上采样)，再卷积，不用转置卷积的函数，为什么呢？然后我就找了网上的各种博客，知乎，终于懂了，现在总结一下。

反卷积的各种叫法

• Deconvolutional反卷积
• Transposed Convolution转置卷积
• inverse Convolution逆卷积

以上是反卷积在CNN中的各种叫法，可代表同一个东西。其实反卷积(Deconvolution)比较容易引起误会，转置卷积(Transposed Convolution)是一个更为合适的叫法。它不同于信号处理中的反卷积deconvolution，网络中的反卷积只能恢复图像尺寸，不能恢复数值。（也就是用一个学习到的卷积核转置做反卷积，不可能得到原来的输入图像，但是得到的图像可以代表原图的部分特征。具体可见论文【1】）【1】Visualizing and Understanding Convolutional Networks

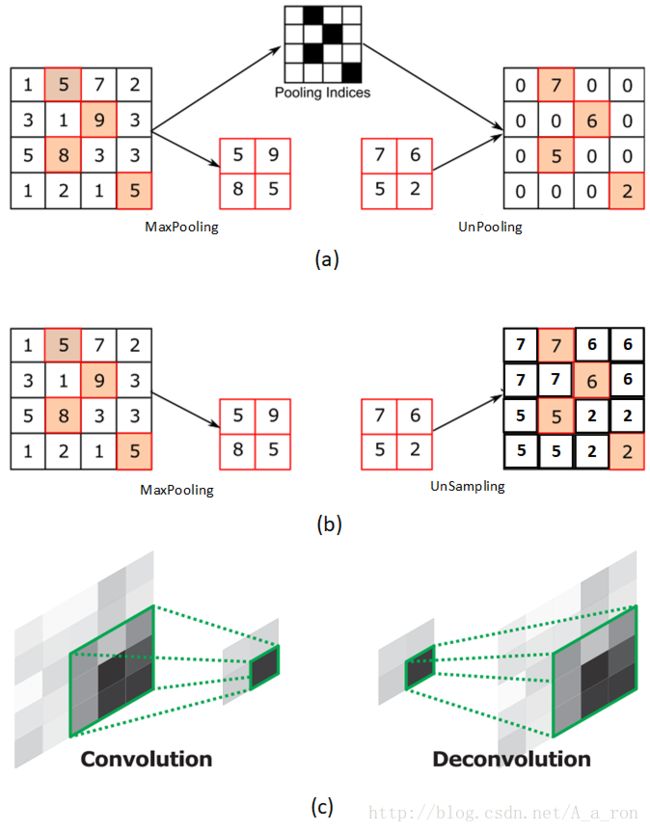
为了避免混淆，再说三个概念：

• Deconvolutional反卷积
• unsampling上采样
• unpooling反池化

这三个概念是不同的，面试时也可能会问到，但都属于上采样（upsample）（注意是up,不是un) 反卷积可以看成是一个可学习的上采样。

常见的上采样方法有双线性插值、转置卷积（反卷积）、上采样（unsampling）和上池化（unpooling） 注意，这里的上采样与unsampling是有区别的，“上采样upsample”这个词代表意义更广， 而unsampling是一个方法。keras、pytorch框架中专门的Upsample函数是指各种“插值算法”， 其中unsampling就是最近邻插值。

反卷积的原理

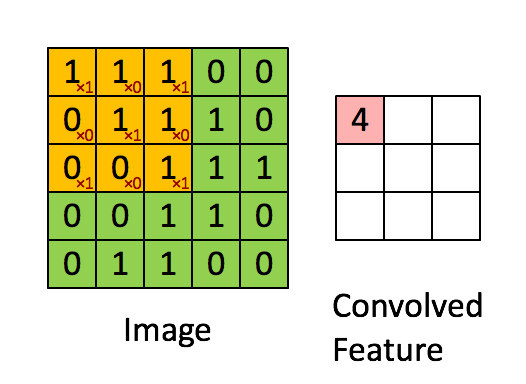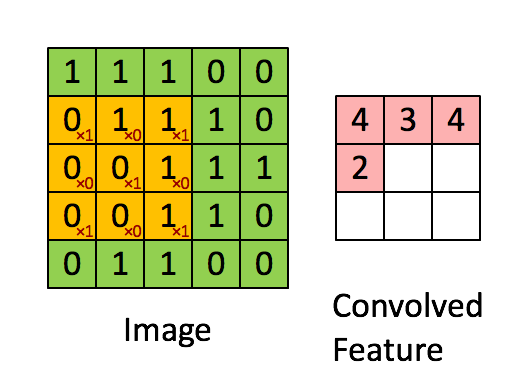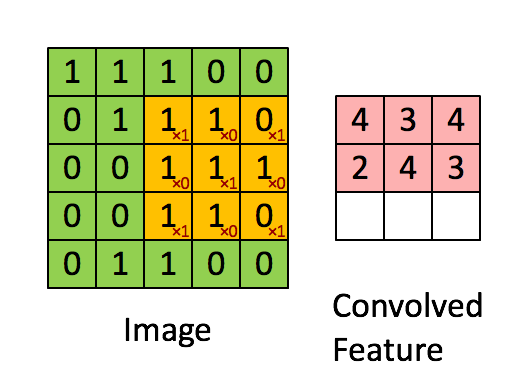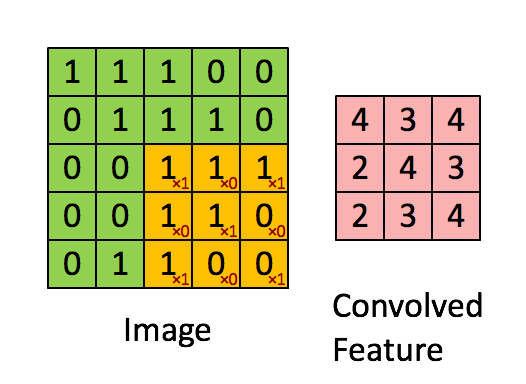
正向卷积的实现过程

矩阵实现：

输入图像尺寸为4*4，卷积核kernel为3*3，步长strides=1，填充padding=0

（1）

（2）把3*3的kernel展成C，以便于与输入向量相乘

矩阵相乘后，（4*16）*（16*1）=（4*1），把(4,1)的结构再展成(2,2)，最后得到的应该是一个2*2大小的feature map

（简化版，具体可参考https://blog.csdn.net/loveliuzz/article/details/84071246）

原理图：

输入图像为5*5，卷积核kernel为3*3，步长strides=1，填充padding=0

转置卷积的实现过程

• 反卷积是一种特殊的正向卷积
• 通俗的讲，就是原矩阵补0+卷积。先按照一定的比例通过补0来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

矩阵实现：

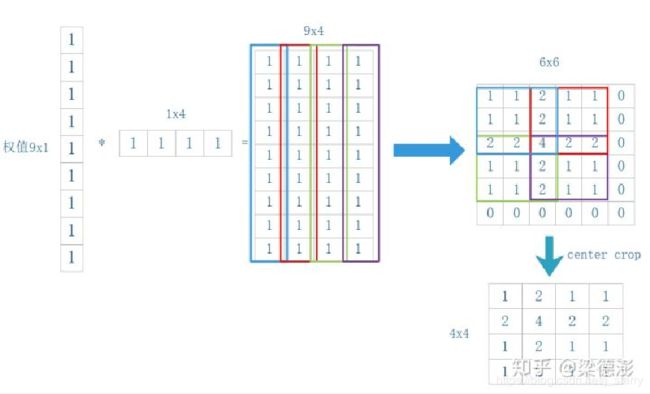
输入图像尺寸为2*2，卷积核kernel为3*3，步长strides=2，填充padding=1

中间结果矩阵大小为9x4，然后把每一列reshape成 3x3 大小然后往6x6输出上累加，最后再crop出中间部分，就得到结果了

参考知乎：（怎样通俗易懂地解释反卷积？ - 梁德澎的回答 - 知乎 https://www.zhihu.com/question/48279880/answer/838063090）

原理图

输入图像尺寸为3*3，卷积核kernel为3*3，步长strides=2，填充padding=1

与正向卷积不同的是，要先根据步数strides对输入的内部进行填充，这里strides可以理解成输入放大的倍数，而不能理解成卷积移动的步长，由上面的原理图可知，是先填充原图，再以步长为1滑动的。

所以说转置卷积的本质就是内部填0+卷积运算

但为什么现在有些代码会用upsample+卷积代替转置卷积呢？

转置卷积的弊端

关于这一节，可主要参考网址（https://distill.pub/2016/deconv-checkerboard/）

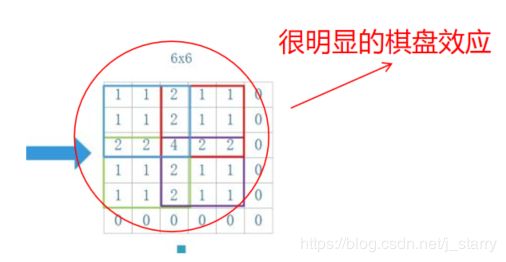
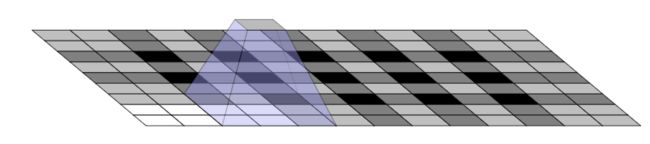
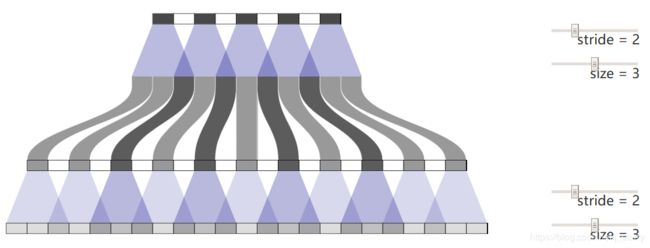
棋盘效应也叫混叠效应，如果参数配置不当，很容易出现输出feature map带有明显棋盘状的现象，以下是原因：

当stride为2的时候，kernel是奇数就会出现网格

3*3的卷积核

5*5的卷积核

当stride为2的时候，kernel是偶数就不会出现网格

2*2的卷积核

4*4的卷积核，只有边缘会有影响

使用能被stride整除的kernel size会抑制棋盘效应。那直接用能被整除的不就行了？错，虽然这样能避免一点，但不能解决根本！（后面举例）【2】【3】

如果是多层堆叠反卷积的话而参数配置又不当，那么棋盘状的现象就会层层传递

所以当使用反卷积的时候参数配置需要特别的小心，mask rcnn的反卷积尺寸就是2*2，步长stride为2的

为了避免混叠效应做的一些尝试

参考【3】

尝试1：使得卷积核大小(4)能被步长(2)整除，但卷积核权重的学习不均匀也会导致伪影现象

尝试2：调整卷积核的权重，适当加大重叠部分少的权重，虽然理论有效，但在实际操作中，不仅有困难也会减弱模型的表达力

尝试3：在反卷积后面，再接一个步长为1的卷积，可以稍微抑制棋盘效应，但效果有限

尝试4（正确的尝试）：调整图像大小（使用最近邻插值或双线性插值），然后执行卷积操作。这似乎是一种自然的方法，大致相似的方法在图像超分辨率方面表现良好

所以说现在大多数论文会用upsample+conv的操作代替转置卷积，下面看一下这两种方法的实验对比

上两行有很明显的棋盘效应

反卷积的应用

反卷积网络可应用在几个方面：（参考：如何理解深度学习中的deconvolution networks？ - 谭旭的回答 - 知乎 https://www.zhihu.com/question/43609045/answer/132235276）

1、卷积稀疏编码。反卷积网络最先在一篇用于无监督学习的重构图像网络中使用。

2、CNN可视化。主要是可视化卷积：将CNN学习到的feature map作为输入，用得到这些feature map的卷积核，取转置作为反卷积块，将图片特征从feature map空间转化到pixel空间，以发现是哪些pixel激活了特定的feature map，达到分析理解CNN的目的。【1】

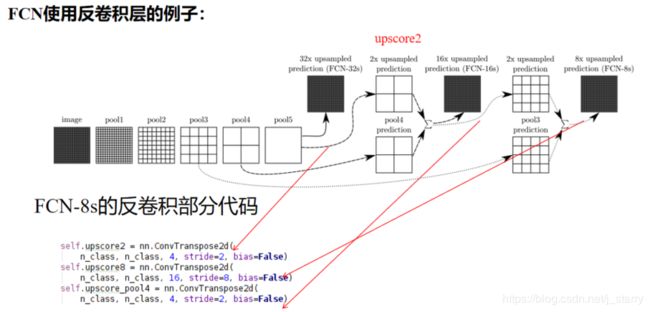
3、upsampling.也就是用于上采样，比如FCN全卷积网络

主要讲3，如FCN，下面通过pytorch代码看它如何实现的反卷积（转置卷积）

扩大几倍，步长就是几，卷积核设置成步长的2倍

在u-net中的反卷积指的是“上采样+卷积”

 

【1】Visualizing and Understanding Convolutional Networks

【2】https://distill.pub/2016/deconv-checkerboard/   对棋盘效应的解释

【3】https://blog.csdn.net/u013289254/article/details/98980517 反卷积(Deconvolution)与棋盘效应(Checkerboard Artifacts)

【4】如何理解深度学习中的deconvolution networks？ - 谭旭的回答 - 知乎 https://www.zhihu.com/question/43609045/answer/132235276

【5】怎样通俗易懂地解释反卷积？ - 梁德澎的回答 - 知乎 https://www.zhihu.com/question/48279880/answer/838063090