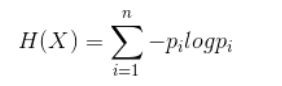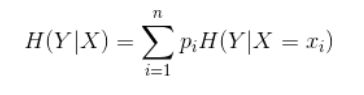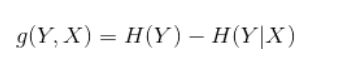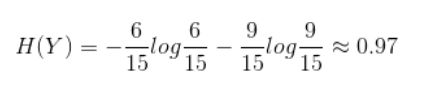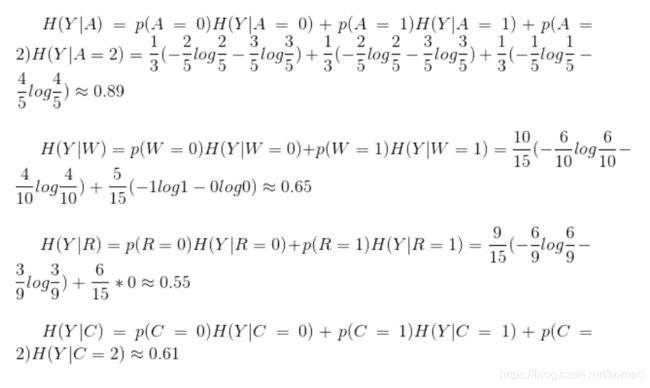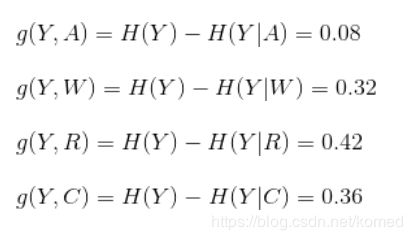机器学习算法--分类决策树（ID3算法）--超详细

分类决策树

在学习分类决策树之前，我们先换个角度来观察我们的世界，我们原本的世界一切都是有自己的固定含义的，对吧，树就是树，花就是花。现在我们将所有的这些概念都扔掉！没错，就是扔掉。将一切的东西开始分解，分解成一个个特征。就像氧气，它的组成是O2，于是它的特征就是O（O原子）和2（2个）。在不知道这两个特征之前，关于氧气的一切都是混乱的，不确定的，也就是熵是最大的，当我们知道了氧气是由氧原子组成，这是关于氧气的概念的熵开始减小，当我们知道是由两个氧原子组成的时候，氧气的概念的熵为0，也就是稳定。于是氧气的概念得以确定，就是O2。用这个方法来看待我们存在的世界，一切的开始都是由熵组成，都是具有不确定性的，当一定的特征聚集在一起的时候，熵也就开始减小，于是也就得出了准确的具有确定性的信息（个人的理解，希望可以帮助到大家）

相关概念知识：

1. 信息熵：

   假设在一个随机变量X之中，X的每个特征值Vi对应一个概率Pi，于是随机变量X 的信息熵计算公式如下
   

2. 条件熵：

   随机变量X给定条件下随机变量Y的条件熵表示为H(Y|X)，表示在已知随机变量X的情况下随机变量Y的不确定性，公式如下（X发生的情况下Y发生的概率的熵–个人理解）：

3. 信息增益：

---

案例：

我们以案例驱动的方式来解释决策树是如何构建出来的，其过程分为两步，特征选择以及决策树的生成。

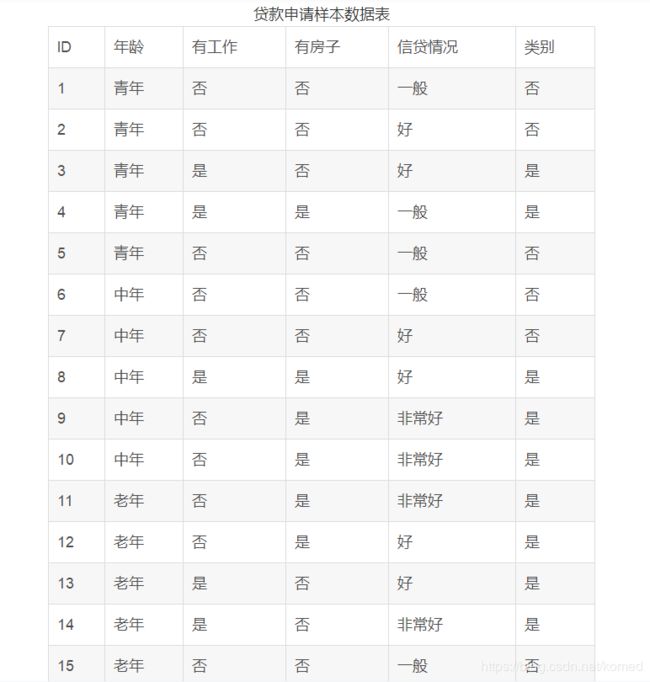
首先我们给定一张数据表，数据表中记录的是一些贷款信息，如下图所示：

我们的任务就是构建一颗决策树来进行判断是否同意某个人的贷款申请。

我们用随机变量来表示类别（0表示否，1表示是）， 表示年龄（0表示青年，1表示中年，2表示老年），是否有工作（0表示否，1表示是），表示是否有房子（0表示否，1表示是），表示信贷情况（0表示一般，1表示好，2表示非常好）后面代码表示与这里一致

根节点包含的样本：所有样本

根节点信息熵：

根节点各个特征的条件熵：

计算信息增益：

因此可以确定，当分支特征为R（即是否有房子）时带来的信息增益最大，因此根节点的分支特征选择为是否有房子，分为左右两支，左子节点中的数据集为没有房子的样本，右子节点的数据集为有房子，之后以此类推便构建出了决策树模型。

（案例来源链接：https://blog.csdn.net/yy2050645/article/details/81212681）

---

代码实战！！！

加载数据

from math import log

def creatDataSet():
    # 数据集
    dataSet=[[0, 0, 0, 0, 'no'],
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    #分类属性
    labels=['年龄','有工作','有房子','信贷情况']
    #返回数据集和分类属性
    return dataSet,labels

测试效果图：

计算标准熵：

def calcShannonEnt(dataSet):
    num_data = len(dataSet)
    shannonEnt = 0.0
    # print(num_data)
    label_count = {}
    for i in dataSet:
        label = i[-1]
        if label not in label_count.keys():
            label_count[label] = 0
        label_count[label]+=1

    for key in label_count.keys():
        Prob = float(label_count[key])/num_data
        shannonEnt-=Prob*log(Prob,2)
    return shannonEnt

效果如图：

计算条件熵、信息增益以及比较出最大的信息增益，代码如下

def splitDataSet(dataSet, axis, value):#划分子集，来求条件熵
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            #reducedFeatVec = featVec[:axis]
            #reducedFeatVec.extend(featVec[axis + 1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
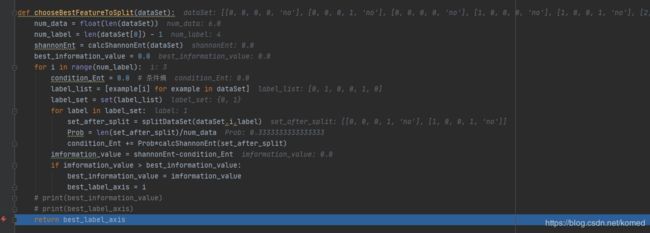
def chooseBestFeatureToSplit(dataSet):
    num_data = float(len(dataSet))
    num_label = len(dataSet[0]) - 1
    shannonEnt = calcShannonEnt(dataSet)
    best_information_value = 0.0#将最佳信息增益初始化为0
    for i in range(num_label):
        condition_Ent = 0.0  # 初始化条件熵为0
        label_list = [example[i] for example in dataSet]
        label_set = set(label_list)
        for label in label_set:
            set_after_split = splitDataSet(dataSet,i,label)
            Prob = len(set_after_split)/num_data
            condition_Ent += Prob*calcShannonEnt(set_after_split)#对应条件熵的计算公式
        imformation_value = shannonEnt-condition_Ent #计算信息增益的公式
        if imformation_value > best_information_value:#比较出最佳信息增益
            best_information_value = imformation_value
            best_label_axis = i
    return best_information_value

现在我们需要的数据都已经处理完成，加下来面对的问题就是决策树构建问题了：

关于决策树的构建，我们有三种算法：

1. ID3（本次需要掌握的算法）
2. C4.5（后面再回到树的时候会详细讲解）
3. CART（后面再回到树的时候会详细讲解）

ID3算法：

核心：以每个结点上的信息增益为选择的标准来递归的构建决策树

现在我们来创造我们的决策树，代码如下

def createTree(dataSet,label):
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    # print(bestFeat,bestFeatLabel)
    mytree = {bestFeatLabel:{}}
    del(label[bestFeat])
    clasify_label_value = [example[bestFeat] for example in dataSet]
    set_clasify_label_value = set(clasify_label_value)
    for value in set_clasify_label_value:
        new_label = label[:]
        mytree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),new_label)
    return mytree

运行结果如图：

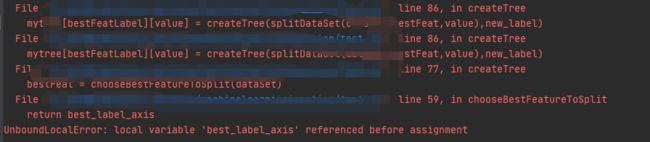
现在不是预想中的顺利得出结果了。。。那我们就来解决掉这个烦人的东西！！

IDEA的DEBUG功能是真的值得打call，太好用了。通过提示，我们来到错误的地方

翻译一下报错信息：

可以知道这个变量没有赋值，但是明明有写赋值语句，所以只有一个可能就是我们赋值语句在if中，但是条件不符合，无法顺利赋值。最后顺藤摸瓜，成功找到根源是因为在递归的过程中，标准熵变成了0，于是增益也变成了0，最佳增益也被初始化为0，自然无法区分谁大谁小。

但是我们不要忘记了，熵，代表的是不确定程度，当熵变成0的时候，代表着我们已经可以确定某样东西了，也就代表着我们的答案出来了。我们重看标准熵的公式，熵等于0，就代表着Pi为0或者log为0，但是当Pi为0时，log为负无穷，自然不可能，所以唯一的可能性就是log为0了，那也就代表着Pi为1，即剩下的都是同一种元素。所以我们在每一轮对决策树的构造中，都加入一个判断，增强我们代码的健壮性。代码如下：

    class_list = [example[-1] for example in dataSet]
    if class_list.count(class_list[0]) == len(class_list): #count() 方法用于统计某个元素在列表中出现的次数。
        return class_list[0]

最终代码如下：

def createTree(dataSet,label):
    class_list = [example[-1] for example in dataSet]
    if class_list.count(class_list[0]) == len(class_list): #count() 方法用于统计某个元素在列表中出现的次数。
        return class_list[0]
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    # print(bestFeat,bestFeatLabel)
    mytree = {bestFeatLabel:{}}
    del(label[bestFeat])
    clasify_label_value = [example[bestFeat] for example in dataSet]
    set_clasify_label_value = set(clasify_label_value)
    for value in set_clasify_label_value:
        new_label = label[:]
        mytree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),new_label)
    return mytree

加入main：

if __name__=='__main__':
    dataSet,labels=creatDataSet()
    mytree = createTree(dataSet,labels)
    print(mytree)

我们再次运行：

CONGRATULATION!!!

成功形成了我们的决策树~~~

艾玛，累死我啦。今天就写到这了，有啥补充的，大家可以在评论区留言哦，这是我最近复习的时候的一点小成果，分享给大家，希望可以帮助到你们呀~~