AC自动机(trie图版)
AC自动机是一个多模字符串匹配的自动机(网上说的),主要作用是在一个长串中同时进行多个字符串的匹配
基础芝士:
trie树(字典树)
烤馍片kmp单模字符串匹配
如果不会的建议去网上学一下(本篇讲解略过)
这里重点讲一讲AC自动机
(由于本蒟蒻不会指针,所以所有算法一律不使用指针,请神犇们谅解)
例:luogu3796 AC自动机(加强版)
其实AC自动机就是在trie树上构造KMP的next指针(在AC自动机中叫fail指针),然后进行匹配
举个例子:
模式串:
abab
abb
bab
匹配串:
aaabbbabababbba
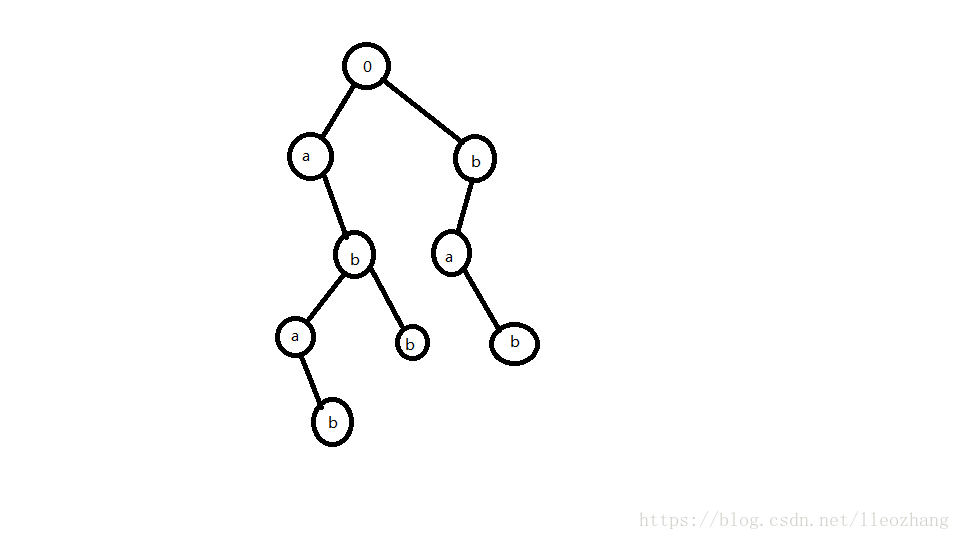
AC自动机第一步:建立trie树!
建树代码如下,基本和trie树代码接近:
void buildtree(char *p)
{
int l=strlen(p);
int now=0;
for(int i=0;i接下来我们考虑构造fail指针
fail指针的含义其实就是:如果在这一位上失配了,那么整个串不必从头开始,而是直接从中间的某处开始继续在失配处匹配即可
由于这是一棵trie树,所以我们可以考虑基于bfs进行构造
首先,如果一开始就失配,那就没啥可说的了,直接返回最大的根节点,所以在构造trie树时一般从1开始,0作为虚节点为根
代码如下:
queue M;
for(int i=1;i<=26;i++)
{
if(tree[0].to[i])
{
M.push(tree[0].to[i]);
tree[tree[0].to[i]].fall=0;
}
} 接下来,我们就可以进行bfs了
这里也是整个AC自动机中最复杂的地方
对于每个点,我们枚举他的每一个to指针,然后分类讨论:
①:这个to节点存在
(什么叫存在?比如上面的trie树,根据字符集来讲,每个节点都应该有两个儿子,可是事实上大部分节点都只有一个儿子,那么有的这个儿子就叫存在,没有就叫不存在)
那么,这个to的fail指针应该指向他父节点的fail指针指向节点所指向的对应的to(读二十遍)
先放代码,再解释,否则不好懂
if(tree[u].to[i])
{
tree[tree[u].to[i]].fall=tree[tree[u].fall].to[i];
M.push(tree[u].to[i]);
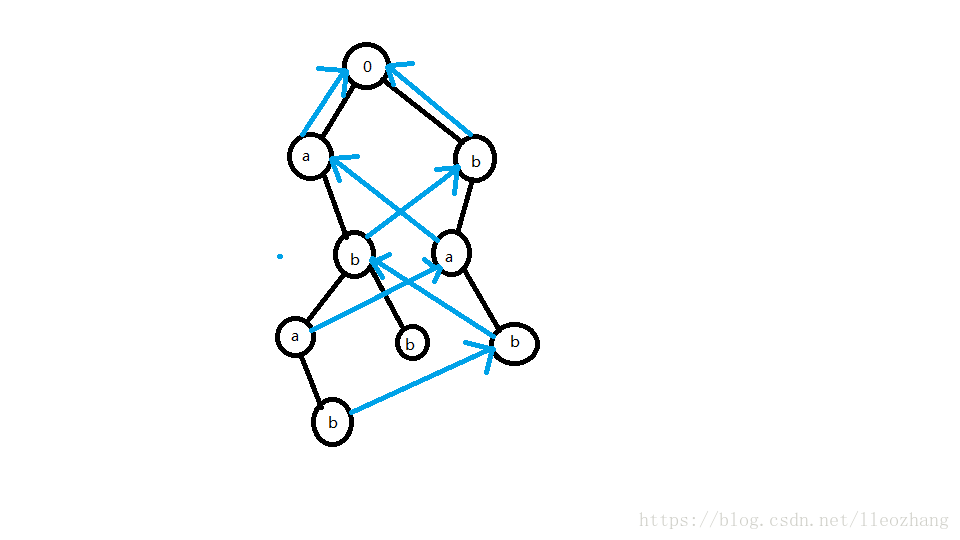
}解释一下,就像这样:
其中蓝色的线为fail指针
发现什么了吗?
一个点fail指针所指向的点所在字符串的前缀一定是这个点所在字符串的子串!
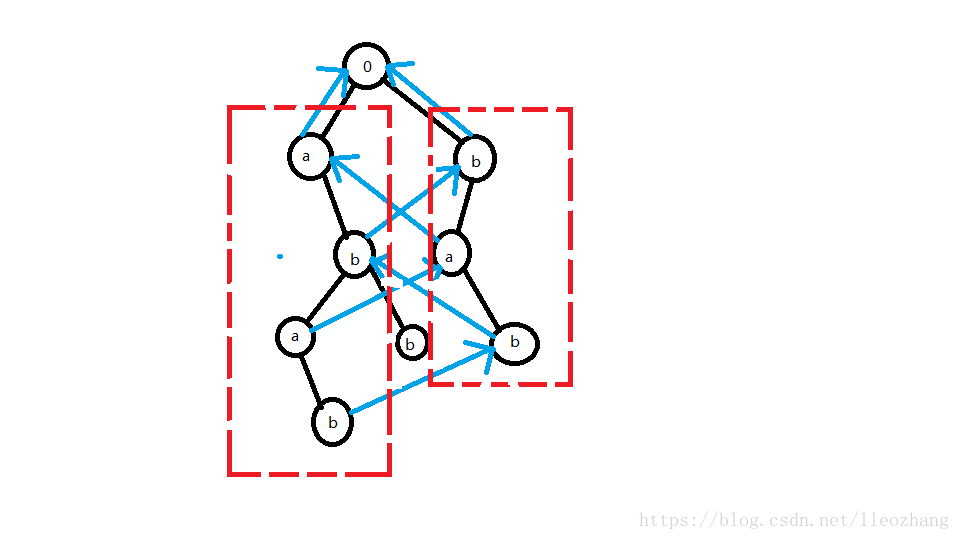
举个例子:
如图所示,右边红色框里的字符串的前缀是左边红色字符串的一个子串,因为左边的b指向了右边的b
(当然,这个前缀理论仅适用于fail指针指向的节点之前的前缀,而之后的是无法保证的)
但是我们会发现一个bug:看到第二个串的最后一个b了吗?他的fail指针应该指向他父节点的fail指针指向节点的对应节点,可是..没有这个节点啊...
直接指回根节点?
这不太好
因为明明有能匹配上的啊
所以我们要利用trie图思想了。
trie图与AC自动机少数的不同就是trie图会补全所有的子节点,补全方法是指向这个点父节点的fail指针指向节点的对应节点
else
{
tree[u].to[i]=tree[tree[u].fall].to[i];
}所以这也就是上面所述的分类讨论的第二种情况:如果这个节点不存在,那么要把这个节点的指针建起来
这样就可以指了
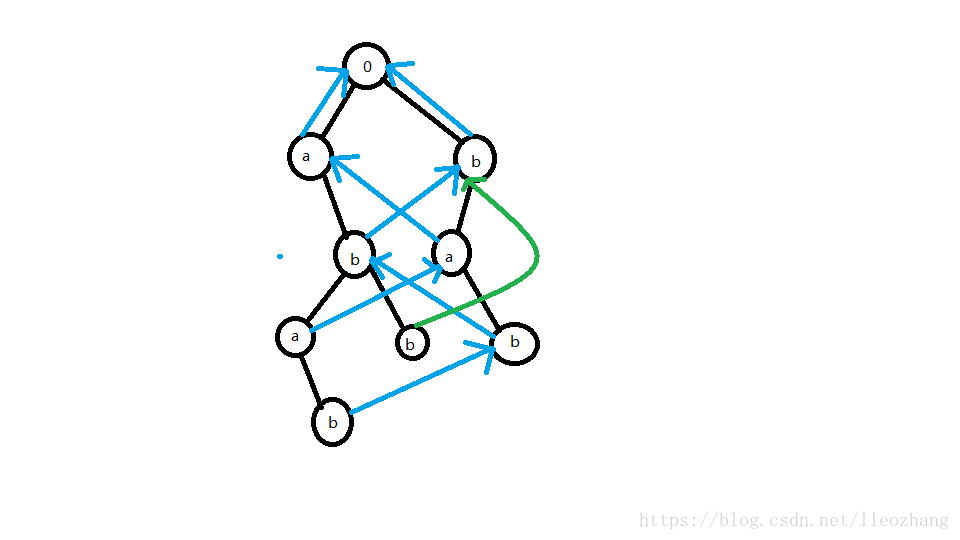
最后构造好的fail指针长这样:
其中绿色的是特殊构造出来的fail指针
fail指针都完事了,接下来就好办了。
我们将模式串在这个AC自动机上跑
查询操作:
int query(char *p)
{
int l=strlen(p);
int ans=0;
tot=0;
int now=0;
for(int i=0;ians)
{
memset(ret,0,sizeof(ret));
tot=0;
ret[++tot]=temp;
ans=tree[temp].ed;
}else if(tree[temp].ed==ans)
{
ret[++tot]=temp;
}
if(tree[temp].ed)
{
tree[temp].ed++;
}
temp=tree[temp].fall;
}
}
return ans;
} 稍微解释一下,就是顺着trie树跑匹配串,根据上文所述fail指针的性质,每次向前找一个前缀使得这个前缀是这个匹配串的子串,于是我们总是能找到整个串是这个字符串的子串
还有一步操作很重要,即上面的最后一个if,这一步的操作目的在于累计某个串被匹配上的次数
这样就完事了
贴代码:
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
struct Trie
{
int to[27];
int fa;
int fall;
int ca;
int ed;
}tree[1000005];
int ret[155];
char s[1000005];
int cnt=0;
int tot=0;
void buildtree(char *p)
{
int l=strlen(p);
int now=0;
for(int i=0;i M;
for(int i=1;i<=26;i++)
{
if(tree[0].to[i])
{
M.push(tree[0].to[i]);
tree[tree[0].to[i]].fall=0;
}
}
while(!M.empty())
{
int u=M.front();
M.pop();
for(int i=1;i<=26;i++)
{
if(tree[u].to[i])
{
tree[tree[u].to[i]].fall=tree[tree[u].fall].to[i];
M.push(tree[u].to[i]);
}else
{
tree[u].to[i]=tree[tree[u].fall].to[i];
}
}
}
}
int query(char *p)
{
int l=strlen(p);
int ans=0;
tot=0;
int now=0;
for(int i=0;ians)
{
memset(ret,0,sizeof(ret));
tot=0;
ret[++tot]=temp;
ans=tree[temp].ed;
}else if(tree[temp].ed==ans)
{
ret[++tot]=temp;
}
if(tree[temp].ed)
{
tree[temp].ed++;
}
temp=tree[temp].fall;
}
}
return ans;
}
bool cmp(int a,int b)
{
return a