单电源运放滤波器设计

在很多情况中，为了阻挡由于虚地引起的直流电平，在 运放的输入端串入了电容。这个电容实际上是一个高通滤波器，在某种意义上说，像这样的单电源运放电 路都有这样的电容。设计者必须确定这个电容的容量必须要比电路中的其他电容器的容量大 100倍以上。 这样才可以保证电路的幅频特性不会受到这个输入电容的影响。如果这个滤波器同时还有放大作用，这个 电容的容量最好是电路中其他电容容量的 1000倍以上。如果输入的信号早就包含了 VCC/2的直流偏置， 这个电容就可以省略。

 

这些电路的输出都包含了 VCC/2的直流偏置，如果电路是最后一级，那么就必须串入输出电容。

 

这里有一个有关滤波器设计的协定，这里的滤波器均采用单电源供电的运放组成。滤波器的实现很简单，

 

但是以下几点设计者必须注意：

1.滤波器的拐点(中心)频率

2.滤波器电路的增益

3.带通滤波器和带阻滤波器的的 Q值

4.低通和高通滤波器的类型(Butterworth、Chebyshev、Bessell)

 

不幸的是要得到一个完全理想的滤波器是无法用一个运放组成的。即使可能，由于各个元件之间的负杂互 感而导致设计者要用非常复杂的计算才能完成滤波器的设计。通常对波形的控制要求越复杂就意味者需要 更多的运放，这将根据设计者可以接受的最大畸变来决定。或者可以通过几次实验而最终确定下来。如果 设计者希望用最少的元件来实现滤波器，那么就别无选择，只能使用传统的滤波器，通过计算就可以得到 了。

 

一、一阶滤波器

 

一阶滤波器是最简单的电路，他们有 20dB每倍频的幅频特性

 

1、低通滤波器

 

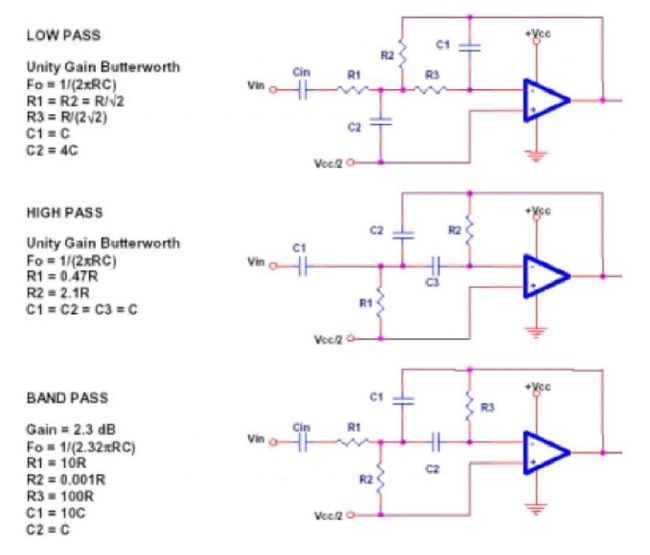
典型的低通滤波器如图十三所示。

 

图十三

 

2、高通滤波器

 

典型的高通滤波器如图十四所示。

 

图十四

 

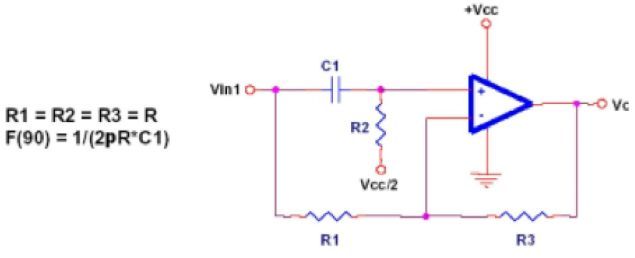
3、文氏滤波器

 

文氏滤波器对所有的频率都有相同的增益，但是它可以改变信号的相角，同时也用来做相角修正电路。图 十五中的电路对频率是 F的信号有 90度的相移，对直流的相移是 0度，对高频的相移是 180度。

 

图十五

 

二、二阶滤波器

 

二阶滤波电路一般用他们的发明者命名。他们中的少数几个至今还在使用。有一些二阶滤波器的拓扑结构

 

可以组成低通、高通、带通、带阻滤波器，有些则不行。这里没有列出所有的滤波器拓扑结构，只是将那

 

些容易实现和便于调整的列了出来。

 

二阶滤波器有 40dB每倍频的幅频特性。

 

通常的同一个拓扑结构组成的带通和带阻滤波器使用相同的元件来调整他们的 Q值，而且他们使滤波器在 Butterworth和 Chebyshev滤波器之间变化。必须要知道只有 Butterworth滤波器可以准确的计算出拐点 频率，Chebyshev和 Bessell滤波器只能在 Butterworth滤波器的基础上做一些微调。

 

我们通常用的带通和带阻滤波器有非常高的 Q值。如果需要实现一个很宽的带通或者带阻滤波器就需要用 高通滤波器和低通滤波器串连起来。对于带通滤波器的通过特性将是这两个滤波器的交叠部分，对于带阻 滤波器的通过特性将是这两个滤波器的不重叠部分。

 

这里没有介绍反相 Chebyshev和 Elliptic滤波器，因为他们已经不属于电路集需要介绍的范围了。

 

不是所有的滤波器都可以产生我们所设想的结果――比如说滤波器在阻带的最后衰减幅度在多反馈滤波器 中的会比在 Sallen-Key滤波器中的大。由于这些特性超出了电路图集的介绍范围，请大家到教科书上去 寻找每种电路各自的优缺点。不过这里介绍的电路在不是很特殊的情况下使用，其结果都是可以接受的。

 

1、Sallen-Key滤波器

 

Sallen-Key滤波器是一种流行的、广泛应用的二阶滤波器。他的成本很低，仅需要一个运放和四个无源器 件组成。但是换成 Butterworth或 Chebyshev滤波器就不可能这么容易的调整了。

 

这个电路是一个单位增益的电路，改变Sallen-Key滤波器的增益同时就改变了滤波器的幅频特性和类型。 实际上 Sallen-Key滤波器就是增益为 1的 Butterworth滤波器。

 

图十六

 

2、多反馈滤波器

 

多反馈滤波器是一种通用，低成本以及容易实现的滤波器。不幸的是，设计时的计算有些复杂，在这里不 作深入的介绍。如果需要的是一个单位增益的 But terworth滤波器，那么这里的电路就可以给出一个近似的结果。

 

图十七

 

3、双 T滤波器

 

双 T滤波器既可以用一个运放也可仪用两个运放实现。他是建立在三个电阻和三个电容组成的无源网络上 的。这六个元件的匹配是临界的，但幸运的是这仍是一个常容易的过程，这个网络可以用同一值的电阻和 同一值的电容组成。用图中的公式就可以同时的将 R3和 C3计算出来。应该尽量选用同一批的元件，他们 有非常相近的特性。

 

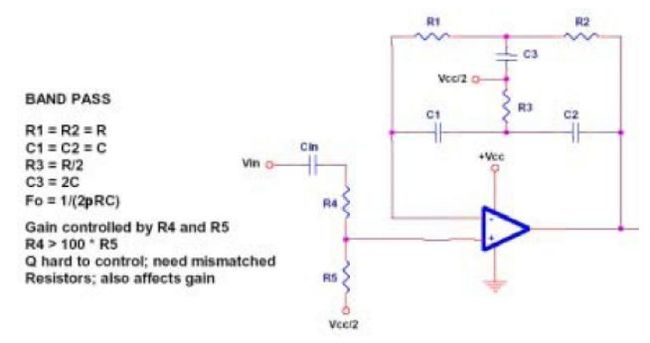
4、单运放实现

 

图十八

 

如果用参数非常接近的元件组成带通滤波器，就很容易发生振荡。接到虚地的电阻最好在 E-961%系列 中选择，这样就可以破坏振荡条件。

 

图十九

 

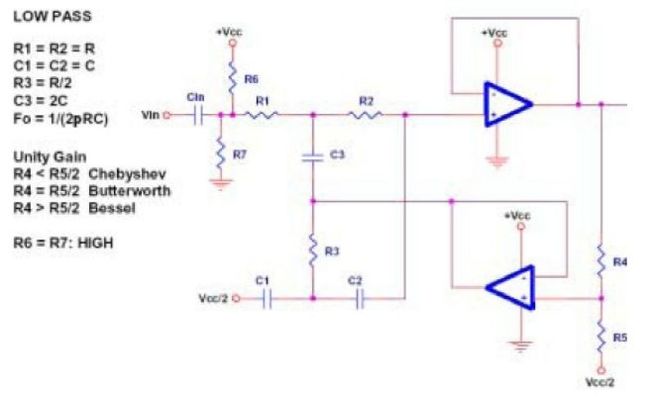
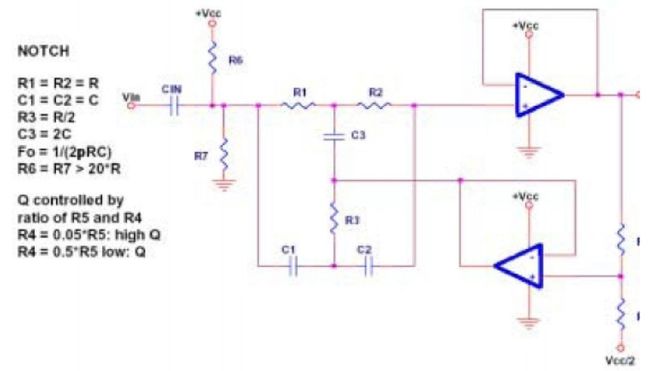
5、双运放实现

 

典型的双运放如图 20到图 22所示

 

图二十

 

图二十一

 

图二十二

 

 

‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧  END  ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧