LeetCode 第 187 场周赛(1336/3107,前43.0%)
文章目录
- 1. 比赛结果
- 2. 题目
- 1. LeetCode 5400. 旅行终点站 easy
- 2. LeetCode 5401. 是否所有 1 都至少相隔 k 个元素 medium
- 3. LeetCode 5402. 绝对差不超过限制的最长连续子数组 medium
- 4. LeetCode 5403. 有序矩阵中的第 k 个最小数组和 hard
1. 比赛结果
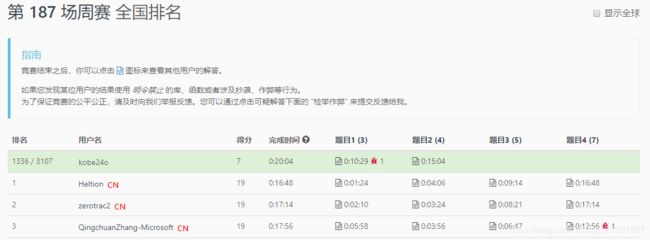
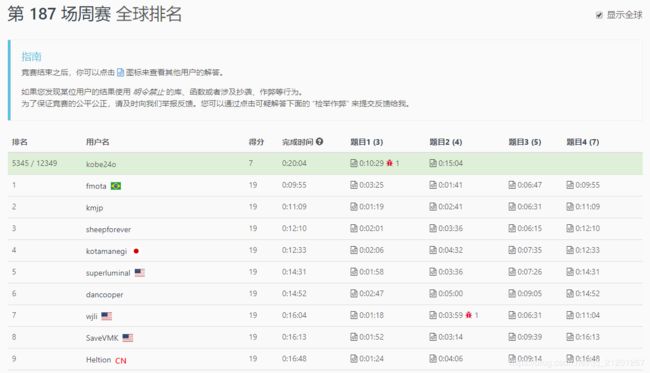
15分钟做出来了 1、2 题,第3题卡了,第4题没做,继续加油!冲啊!
全国排名:1336 / 3107,43.0%;全球排名:5345 / 12349,43.3%
2. 题目
1. LeetCode 5400. 旅行终点站 easy
题目链接
给你一份旅游线路图,该线路图中的旅行线路用数组 paths 表示,其中 paths[i] = [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。
请你找出这次旅行的终点站,即没有任何可以通往其他城市的线路的城市。
题目数据保证线路图会形成一条不存在循环的线路,因此只会有一个旅行终点站。
示例 1:
输入:paths = [["London","New York"],["New York","Lima"],["Lima","Sao Paulo"]]
输出:"Sao Paulo"
解释:从 "London" 出发,最后抵达终点站 "Sao Paulo" 。
本次旅行的路线是 "London" -> "New York" -> "Lima" -> "Sao Paulo" 。
示例 2:
输入:paths = [["B","C"],["D","B"],["C","A"]]
输出:"A"
解释:所有可能的线路是:
"D" -> "B" -> "C" -> "A".
"B" -> "C" -> "A".
"C" -> "A".
"A".
显然,旅行终点站是 "A" 。
示例 3:
输入:paths = [["A","Z"]]
输出:"Z"
提示:
1 <= paths.length <= 100
paths[i].length == 2
1 <= cityAi.length, cityBi.length <= 10
cityAi != cityBi
所有字符串均由大小写英文字母和空格字符组成。
解答:
class Solution {
public:
string destCity(vector<vector<string>>& paths) {
unordered_set<string> dist;
unordered_set<string> start;
for(auto p : paths)
{
start.insert(p[0]);//加入起点
if(dist.count(p[0]))//目的地包含出发
dist.erase(p[0]);//删除
if(!start.count(p[1]))//不是起点
dist.insert(p[1]);//插入终点集合
else//p[1]是起点
{
if(dist.count(p[1]))
dist.erase(p[1]);//终点中删除
}
}
return *dist.begin();
}
};
32 ms 11.6 MB
赛后另解:图的出入度概念,终点,只有入度,出度为0
class Solution {
public:
string destCity(vector<vector<string>>& paths) {
unordered_map<string,int> in;
unordered_map<string,int> out;
for(auto p : paths)
{
out[p[0]]++;
in[p[1]]++;
}
for(auto in_ : in)
{
if(out[in_.first]==0)
return in_.first;
}
return "";
}
};
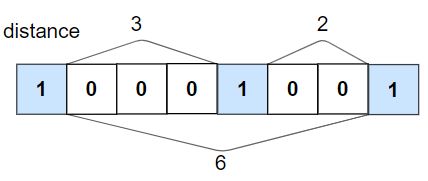
2. LeetCode 5401. 是否所有 1 都至少相隔 k 个元素 medium
题目链接
给你一个由若干 0 和 1 组成的数组 nums 以及整数 k。
如果所有 1 都至少相隔 k 个元素,则返回 True ;否则,返回 False 。
输入:nums = [1,0,0,0,1,0,0,1], k = 2
输出:true
解释:每个 1 都至少相隔 2 个元素。
示例 2:
输入:nums = [1,0,0,1,0,1], k = 2
输出:false
解释:第二个 1 和第三个 1 之间只隔了 1 个元素。
示例 3:
输入:nums = [1,1,1,1,1], k = 0
输出:true
示例 4:
输入:nums = [0,1,0,1], k = 1
输出:true
提示:
1 <= nums.length <= 10^5
0 <= k <= nums.length
nums[i] 的值为 0 或 1
解答:
- 先把 1 的位置存下来,然后再遍历位置,检查相邻的差值
class Solution {
public:
bool kLengthApart(vector<int>& nums, int k) {
bool flag = true;
int i, count = 0, prev = -1;
vector<int> pos;
for(i = 0; i < nums.size(); ++i)
{
if(nums[i] == 1)
pos.push_back(i);
}
for(i = 0; i < int(pos.size())-1; ++i)
{
if(pos[i+1]-pos[i] <= k)
{
flag = false;
break;
}
}
return flag;
}
};
176 ms 60.2 MB
或者直接遍历,节省空间,
class Solution {
public:
bool kLengthApart(vector<int>& nums, int k) {
int i, prevOneIdx = -1000000;
for(i = 0; i < nums.size(); ++i)
{
if(nums[i] == 1)
{
if(i-prevOneIdx <= k)
return false;
prevOneIdx = i;
}
}
return true;
}
};
184 ms 57.6 MB
3. LeetCode 5402. 绝对差不超过限制的最长连续子数组 medium
题目链接
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
输入:nums = [8,2,4,7], limit = 4
输出:2
解释:所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。
示例 2:
输入:nums = [10,1,2,4,7,2], limit = 5
输出:4
解释:满足题意的最长子数组是 [2,4,7,2],其最大绝对差 |2-7| = 5 <= 5 。
示例 3:
输入:nums = [4,2,2,2,4,4,2,2], limit = 0
输出:3
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9
解题:
- 双指针,滑动窗口,窗口内的数为了快速获取最大最小值,采用multimap存储
- 一旦加入的数跟MAX,MIN做差,不在范围内,左端点向右移动,并删除map内的该值
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
multimap<int,int> m;//value, idx
int i = 0, j, MAX, MIN, maxlen = 1;
for(j = 0; j < nums.size(); ++j)
{
m.insert(make_pair(nums[j],j));
MIN = m.begin()->first;//map有序
MAX = (--m.end())->first;
if(abs(nums[j]-MIN) <= limit && abs(nums[j]-MAX) <= limit)
{
maxlen = max(maxlen, int(m.size()));
}
while(!(abs(nums[j]-MIN) <= limit && abs(nums[j]-MAX) <= limit))
{
auto it = m.lower_bound(nums[i++]);
m.erase(it);
MIN = m.begin()->first;
MAX = (--m.end())->first;
}
}
return maxlen;
}
};
276 ms 47.1 MB
参考 大佬IK哥的解:
自己写了下,采用map计数的方式
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
map<int,int> m;//value, count计数
int i = 0, j = 0, MAX, MIN, maxlen = 1;
while(j < nums.size())
{
m[nums[j]]++;//计数
MIN = m.begin()->first;
MAX = (--m.end())->first;
if(abs(nums[j]-MIN) <= limit && abs(nums[j]-MAX) <= limit)
maxlen = max(maxlen, j-i+1);
else
{
while(!(abs(nums[j]-MIN) <= limit && abs(nums[j]-MAX) <= limit))
{
m[nums[i]]--;
if(m[nums[i]]==0)
m.erase(nums[i]);
i++;
MIN = m.begin()->first;
MAX = (--m.end())->first;
}
}
j++;
}
return maxlen;
}
};
232 ms 39 MB
4. LeetCode 5403. 有序矩阵中的第 k 个最小数组和 hard
题目链接
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。
你可以从每一行中选出 1 个元素形成一个数组。
返回所有可能数组中的第 k 个 最小 数组和。
示例 1:
输入:mat = [[1,3,11],[2,4,6]], k = 5
输出:7
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。
示例 2:
输入:mat = [[1,3,11],[2,4,6]], k = 9
输出:17
示例 3:
输入:mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出:9
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。
示例 4:
输入:mat = [[1,1,10],[2,2,9]], k = 7
输出:12
提示:
m == mat.length
n == mat.length[i]
1 <= m, n <= 40
1 <= k <= min(200, n ^ m)
1 <= mat[i][j] <= 5000
mat[i] 是一个非递减数组
解答:
参考 IK 哥 的解答:
- 暴力解法
- 把第一行跟第二行,两两相加,取最小的 k 个出来
- 把这些再跟第三行两两相加,重复下去
class Solution {
public:
int kthSmallest(vector<vector<int>>& mat, int k) {
vector<int> ans(mat[0]);
int i, j, ki;
for(i = 1; i < mat.size(); ++i)
{
multiset<int> s;
for(j = 0; j < mat[i].size(); ++j)
{
for(ki = 0; ki < ans.size(); ++ki)
s.insert(mat[i][j]+ans[ki]);
}
ans.assign(s.begin(),s.end());
ans.resize(min(k, int(ans.size())));
}
return ans[k-1];
}
};
1736 ms 156.3 MB
优先队列解题
struct cmp
{
bool operator()(const pair<int,vector<int>>& a, const pair<int,vector<int>>& b) const
{
return a.first > b.first;//小顶堆,和小的在堆顶
}
};
class Solution {
public:
int kthSmallest(vector<vector<int>>& mat, int k) {
pair<int,vector<int>> tp;
int i, j, s0 = 0, m = mat.size(), n = mat[0].size(), s;
for(i = 0; i < m; ++i)
s0 += mat[i][0];//最小的和
vector<int> idx(m,0);//每行选取的下标
vector<int> tempidx;
priority_queue<pair<int,vector<int>>, vector<pair<int,vector<int>>>,cmp> q;
q.push({s0,idx});
set<vector<int>> visited;
visited.insert(idx);//访问过了
while(--k)
{
tp = q.top();
s0 = tp.first;
idx = tp.second;
q.pop();
for(i = 0; i < m; ++i)
{
tempidx = idx;
tempidx[i]++;//该行变大一点
if(tempidx[i] < n && !visited.count(tempidx))//没有访问过该状态
{
s = s0-mat[i][idx[i]]+mat[i][idx[i]+1];//DP思路求解下一次的和
visited.insert(tempidx);
q.push({s,tempidx});
}
}
}
return q.top().first;
}
};
568 ms 43.4 MB