剑指offer | 面试题54:二叉搜索树的第k大节点
转载本文章请标明作者和出处
本文出自《Darwin的程序空间》
本文题目和部分解题思路来源自《剑指offer》第二版
![]()
题目
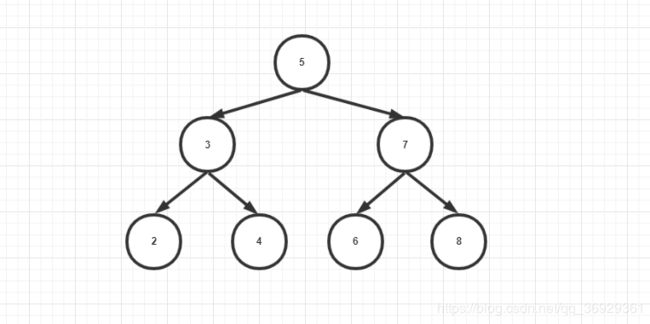
给定一棵二叉搜索树,请找出其中的第k小的结点。例如, 如下图(5,3,7,2,4,6,8) 中,按节点数值大小顺序第三小结点的值为4
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
解题分析
要做这道题,首先我们得十分了解二叉搜索树这个数据结构;
二叉查找树(英语:Binary Search Tree),也称为 二叉搜索树、有序二叉树(Ordered Binary Tree)或排序二叉树(Sorted Binary Tree),是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(\log n)O(logn)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
二叉查找树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉查找树变成一个有序序列,构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望 O(\log n)O(logn),最坏 O(n)O(n)(数列有序,树退化成线性表)。
虽然二叉查找树的最坏效率是 O(n)O(n),但它支持动态查询,且有很多改进版的二叉查找树可以使树高为 O(\log n)O(logn),从而将最坏效率降至 O(\log n)O(logn),如 AVL 树、红黑树等。
横线中来源于leetcode
二叉搜索树,自然是二叉树的一种,而它最主要的特点就是,要不是一棵空树,要不这棵树上所有的节点的右边的所有节点以及子节点都比这个节点要大,并且这棵树上所有的节点的左边的所有节点以及子节点都比这个节点要小;
这种数据结构的一个神奇之处就在于,中序遍历的结果,如果是左子树在前,右子树在后,遍历结果就是由大到小、如果是右子树在前,左子树在后,遍历结果就是由小到大;
这里引出一个概念,中序遍历,注意这个不是只适用于二叉搜索树,这是一种二叉树的遍历方式;还有(前序遍历、后序遍历、宽度优先遍历)等;中序遍历的结果就是,左边的及节点以及子节点永远都先打印,右边的及节点以及子节点永远都后打印(中序遍历一般都是左子树在前,右子树在后),而中序遍历的实现方式就是先递归左子树,再递归右子树;如下附上代码,建议看不懂的同学debug看一下,慢慢理解;
public static void midPrint(TreeNode root) {
if (Objects.nonNull(root)) {
midPrint(root.left);
System.out.println(root.val);
midPrint(root.right);
}
}
再结合二叉搜索树的定义,得出结论,二叉搜索树使用这种遍历方式得到的数字是从小到大的;
如果要从大到小呢?我们只需要先遍历右子树,再遍历左子树即可;
public static void midPrint(TreeNode root) {
if (Objects.nonNull(root)) {
midPrint(root.right);
System.out.println(root.val);
midPrint(root.left);
}
}
到这,希望你已经懂了怎么样从大到小输出一个二叉搜索树;
然后引出我们的第一种解法,递归,其实就是上面那种遍历方式的变形,我们不需要遍历完这个二叉树,我们只需要遍历到第k大的就好,所以我们要定义一个全局变量count为k(如果要是递归中使用局部变量会随着方法的弹栈而变化,不好控制),每遍历到一个节点我们就减一,直到count等于1,这时遍历到的数字就是最大的,我们此时记录答案终止递归,return方法即可;这种方法罕见的在leetcode上内存和时间都击败了100%的JAVA同学;
第二种迭代的方式我是在leetcode上看到一位同学写的,效率实测没有上面的好,但是可以看出楼主对二叉搜索树的理解,我对楼主的原代码做了一定的优化,我也建议大家平时的时候多集思广益,不光会一种解法,更是对这种数据结构的理解层次上的提升;
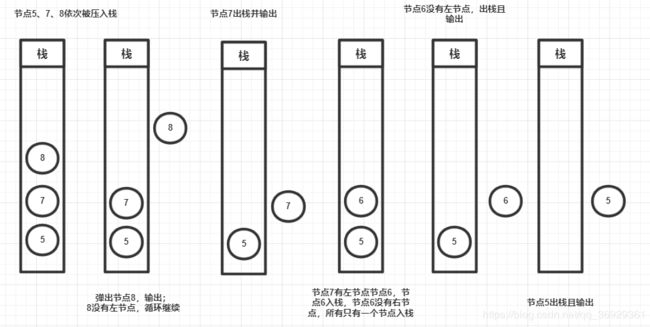
这种迭代的方式使用了栈结构,主要的思想就是,一个节点的右节点一定比这个节点的左子树乃至父节点都大,所以我们需要利用栈结构迭代找到最右边的节点,当右节点遍历完了之后,再看一下这个右节点有没有左子节点(因为这个右节点的左子节点也比这个右子节点的父节点大),左右都遍历完了,再输出这个当前节点,同理,输出完当前节点,再看看当前节点有没有左子节点,没有的话,再回到当前节点的父节点,这样以此类推,就能按照从大到小输出,当然我们只要第k大,所以定义一个常量,当到了第k个直接return即可;如下图为我手画的基于示例图的堆栈执行过程;

代码(JAVA实现)
ps:这里笔者使用的jdk为1.8版本
- 递归(推荐)
class Solution {
int count;
int result = -1;
public int kthLargest(TreeNode root, int k) {
count = k;
kthLargest(root);
return result;
}
public void kthLargest(TreeNode root) {
if (Objects.nonNull(root)) {
kthLargest(root.right);
if (count == 1) {
result = root.val;
count--;
return;
}
count--;
kthLargest(root.left);
}
}
}
- 迭代
class Solution {
public int kthLargest(TreeNode root, int k) {
int count = 1;
Stack<TreeNode> stack = new Stack<>();
while (Objects.nonNull(root) || !stack.empty()) {
while (Objects.nonNull(root)) {
stack.push(root);
root = root.right;
}
TreeNode pop = stack.pop();
if (count == k) {
return pop.val;
}
count++;
root = pop.left;
}
return 0;
}
}
![]()