基于LMS算法的自适应滤波器

LMS（Least Mean Square）

LMS（Least Mean Square），最小均方算法，是一种自适应滤波算法，最早由Widrow和Hoff提出，此算法不需要已知输入信号和期望信号，当前时刻的权重是通过上一个时刻的权重加上负均方误差梯度的比例得到的。权重公式：

β为学习率，或者称为收敛步长，恰当的学习率可以使结果更趋近于真实。▽k是目标函数的梯度。

假设两地通信，说话声音信号single，会因为与噪音noise结合生成新的被干扰的信号input，根据这三个条件设计出符合该假设的滤波器。

利用上面的公式推导得出下面的公式：

分析

使用计算机模拟的方法十分简单，步骤如下：
①创建资料集，产生single和noise的值；

②划分资料集，一部分作为训练LMS模型；另一部分用来检测模型误差大小。

③建立模型，理解LMS算法原理后，可以根据公式建立一个基于LMS的模型：
i 设置权重空间，我们通过公式已经知道权重W是一个一维矩阵，因此用来要设置它的空间大小，这里假设是4，那么初始化的权重是[0, 0, 0, 0]。

ii 设置偏置项b，训练产生的结果为了更加接近原始资料，根据训练的迭代可以得出一个与input存在线性关系的偏置项b，为了不影响训练，初始值设置为0。

④训练模型，导入训练集，设置学习率，LMS模型将会不断调整滤波器全向轮，使权矢量和偏置项接近最优解。

⑤使用模型，训练已经完成，将已有资料导入模型进行处理，然后根据结果来调整参数大小，降低误差。

实现

# python-Noise Cancellation
# coding=utf-8
import numpy
import matplotlib.pyplot as plt
class LMS:
    def __init__(self, vector_size):
        self.size   = vector_size
        self.weight = [0] * vector_size
        self.b      = 0
    def train(self, trainX, trainY, beta = 1e-3):
        step        = len(trainX)
        if step < self.size:
            return
        for i in range(self.size - 1, step):
            x       = trainX[i - self.size + 1: i + 1]
            value   = numpy.sum(self.weight * x)
            error   = trainY[i] - value
            self.weight += 2 * beta * error * x
            self.b      += 2 * beta * error
        return
    def predict(self, input):
        predictY    = [numpy.nan] * (self.size - 1)
        for i in range(self.size - 1, len(input)):
            x       = input[i - self.size + 1: i + 1]
            predictY.append(numpy.sum(self.weight * x) + self.b)
        return predictY
    def evaluate(self, predictY, realY):
        loss = (predictY - realY) ** 2
        MSE = numpy.mean(loss[self.size - 1:])
        return MSE
numpy.random.seed(7)
vector_size = 4
step        = 200
beta        = 1e-4
t           = numpy.mgrid[0 : 2 : (2 - 0) / step]
single      = 2 * numpy.sin(t) + 1.5
v           = numpy.random.normal(0, 1, step)
noise       = (v - 1.34) ** 2 + 5.2
input       = single + noise

train_size  = int(step * 0.7)
test_size   = step - train_size
trainX      = input[0 : train_size]
testX       = input[train_size : step]
trainY      = single[0 : train_size]
testY       = single[train_size : step]

model       = LMS(vector_size)
model.train(trainX, trainY, beta)
train_Pre   = model.predict(trainX)
test_Pre    = model.predict(testX)
train_Cost  = model.evaluate(train_Pre, trainY)
test_Cost   = model.evaluate(test_Pre, testY)
output      = model.predict(input)
cost        = model.evaluate(output, single)
print('train MSE:', train_Cost)
print('test  MSE:', test_Cost)
print('all   MSE:', cost)
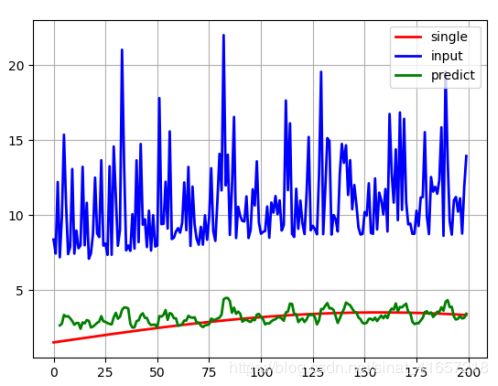
plt.plot(single, 'r-', linewidth=1, label='single')
plt.plot(input,  'b-', linewidth=1, label='input')
plt.plot(output, 'g-', linewidth=1, label='predict')
plt.legend()
plt.grid(True)
plt.show()

绘图结果：

模型效果：
train MSE: 0.42479847238705815
test MSE: 0.22478527148613403
all MSE: 0.3627344052096806

扩大资料集范围：