线段树解决区间问题包括延迟操作以及离散化

线段树简介与分治策略

线段树简介

线段树是一棵二叉树，用来解决区间问题。线段树的每个节点均保存有源数组中某个区间的特征值（最值、区间和、……）。本质上说，线段树是区间问题分治策略的实现模板。

分治策略

考虑如下一个简单的示意图，假设需要求取区间和。此时将整个区间折半分为左子区间与右子区间。关键问题是：如果已知两个子区间的区间和，能不能在$O(1)$时间内求出整个区间的区间和？

答案当然是肯定的。因此区间和问题具备分治的基本条件之一，可分可合。另外，很容易发现划分的终点在于每个子区间只包含源数组的一个元素，此时的区间和就是源数组的元素值，也可以在$O(1)$求出。因此可以在$log$时间内求出区间和。这是一个典型的分治过程。
同理，不仅仅是区间和，区间最值等其他区间特征，只要能够在“合”的时候，以$O(1)$完成的，均可以考虑使用线段树完成。所以，线段树从根本上说是一个分治策略的实现模板。

线段树不能解决的问题

根据上面的思想，反过来可以知道线段树不能解决的问题。考虑这样一个问题：给定区间，求区间内不同元素的总数量是多少。
假设已知左子区间不同元素的数量是3，右子区间不同元素的数量是4，能不能得出结论说整个区间不同元素的数量是7？当然不能。因此这个问题不能用线段树解决。因为强行合并的话，时间复杂度太高。
解决此类问题，可以考虑莫队算法。

线段树的基本操作

线段树的简单示例

仍然考虑区间和问题，假设源数组是一个5元素的数组，元素值分别是$300,100,200,500,400$，则可以建立一个9节点的线段树，源数组与对应的线段树如下：

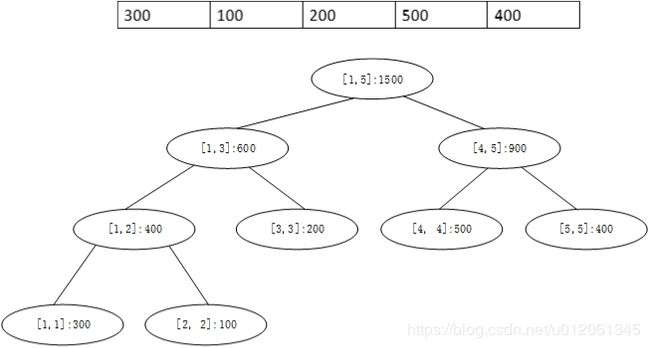
根节点保存整个数组的区间和，即区间$[1,5]$的和是1500。根的两个子节点，左节点保存$[1,3]$的区间和600，右节点保存$[4,5]$的区间和900。以此类推。叶子节点保存单个元素区间的和，例如区间$[1,1]$的和，其实就是源数组第1个元素的值。
从这个图很容易看出线段树的结构规律，父节点保存$[s,e]$的区间和，则左子节点保存$[s,m]$的和，右子节点保存$[m+1,e]$的和。其中，$m=(s+e)/2$。而且，父节点的和等于左子节点加上右子节点。此时，只需代码实现即可。

线段树的基础代码实现

当前最流行的线段树代码实现有3个要点：

1. 用数组实现二叉树
2. 主要操作均采用递归完成
3. 节点不保存$[s,e]$信息，而通过参数传递

前两条是数据结构基础中常见的套路，最后一条则是空间上的一个小优化。因为实际使用的时候，一定是从根节点开始调用的，因此在递归调用时可以把区间信息逐层下传。这样一来，就不需要在二叉树节点本身保存区间信息。
从模块化角度出发，可以将线段树操作划分为辅助操作与建、查、改操作。其中，辅助操作不应该在主函数中调用，主函数只应调用建、查、改。

辅助操作

首先实现线段树的几个辅助操作，包括计算左右子节点、分治中的合操作等。

//用数组保存二叉树
int ST[SIZE<<2];
//计算左子节点与右子节点
inline int lson(int t){return t<<1;}
inline int rson(int t){return lson(t)|1;}
//已知子节点求父节点，即分治中的“合”
void _pushUp(int t){
    ST[t] = ST[lson(t)] + ST[rson(t)];
}

这里要注意线段树一定要开源数组的4倍！！！一般学线段树看了上面的简图后，会不自觉的把线段树与完全二叉树联系起来，认为开二倍即可。这是不正确的。实际上当源数组有6个元素时，二叉树就需要用到第13个节点，超出了二倍范围。当源数组有36个元素时，二叉树需要用到的节点总数就超出了三倍范围。

建树

//t代表线段树节点，[s, e]表示该线段树节点所对应的源数组区间
void build(int t, int s, int e){
    if( s == e ){
        ST[t] = A[s]; //这里可以有一个优化，可以直接输入而无需源数组A
        return;
    }

    int m = ( s + e ) >> 1;
    build(lson(t), s, m);
    build(rson(t), m+1, e);
    _pushUp(t);
}

建树操作有一个优化，一般的代码流程可能是这样：

1. 读入源数组
2. 根据源数组建线段树

注意到线段树的树叶出现的顺序，实际上与源数组顺序一模一样。因此完全不需要分两步，可以直接实施建树操作，然后在树叶处直接读入即可。此时读入的数必然是对应的源数组的元素。换言之，在整个程序中，其实不需要源数组，只需要有线段树即可。
另外，注意到参数列表$(t,s,e)$是一套，建、查、改操作中均是成套使用的。而且在主函数中调用，其实参列表必然是$(1,1,N)$（其中N表示源数组的长度，源数组编号从1开始）。这样设计的话，线段树节点就无需再保存区间信息。

查询

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//[a, b]表示要查询的区间，注意在这一系列递归中[a, b]始终保持不变
int query(int t, int s, int e, int a, int b){
    if( a <= s && e <= b ){
        return ST[t];
    }

    int m = ( s + e ) >> 1;
    int ret = 0;
    if( a <= m ) ret += query(lson(t),s,m,a,b);
    if( m < b ) ret += query(rson(t),m+1,e,a,b); 
    return ret;
}

这是查询区间和的例子，如果是查询区间最值或者是其他，则递归结果与本次返回值之间的关系可能需要进行修改。例如，如果返回区间最大值，则查询操作变为：

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//[a, b]表示要查询的区间，注意在这一系列递归中[a, b]始终保持不变
int query(int t, int s, int e, int a, int b){
    if( a <= s && e <= b ){
        return ST[t];
    }

    int m = ( s + e ) >> 1;
    int ret = 负无穷大;
    if( a <= m ) ret = max(ret, query(lson(t),s,m,a,b));
    if( m < b ) ret = max(ret, query(rson(t),m+1,e,a,b)); 
    return ret;
}

与建树操作类似，$(t,s,e)$是成套的，随着递归调用而不断变化，而与之相对的是$a,b$参数是不变的。想象一下，在主函数中为了查询$[a,b]$的区间和而调用查询函数，随后又在查询函数中进行递归调用。因此这一系列的递归调用都是为了解决区间$[a,b]$的问题，因此这一对参数保持不变。

修改

线段树不但能支持静态区间和等区间问题，还可以支持修改操作。最简单的修改即单点修改，将源数组中指定的一个元素值进行修改。注意源数组是从1开始编号的。

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//该操作表示将源数组第pos位置上的元素值增加delta
void modify(int t, int s, int e, int pos, int delta){
    if( s == e ){
        ST[t] += delta;
        return;
    }

    int m = ( s + e ) >> 1;
    if( pos <= m ) modify(lson(t),s,m,pos,delta);
    else modify(rson(t),m+1,e,pos,delta); 
    _pushUp(t);
}

这是一个增量操作，当然稍加修改也可以修改成$set$操作或者是别的修改操作。

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//该操作表示将源数组第pos位置上的元素值设定为newValue
void modify(int t, int s, int e, int pos, int newValue){
    if( s == e ){
        ST[t] = newValue; //不同的修改操作基本上只需在这里体现即可
        return;
    }

    int m = ( s + e ) >> 1;
    if( pos <= m ) modify(lson(t),s,m,pos,delta);
    else modify(rson(t),m+1,e,pos,delta); 
    _pushUp(t);
}

延迟操作

延迟操作思想

延迟操作是线段树的一个台阶，只有掌握了延迟操作才能体现线段树的强大功能。否则有其他更简单的实现，例如树状数组或者ST算法等。
延迟操作解决的是存在成段修改的情况下，如何快速的进行区间的查询和修改。所谓成段修改，例如将$[1,\frac{7N}{8}]$区间内的元素全部都加1，或者将$[\frac{N}{3},N]$内的元素全部都减2，等等。如果将成段修改操作拆分成若干单点修改，显然时间复杂度会有质的改变，是不能接受的。
延迟操作的基本思路是：对于修改操作，只修改到“适当位置”，剩余应该修改而不修改的位置使用$Lazy$标记“记住”。这个策略称作延迟操作（延迟操作是计算机系统中常见的策略，最常见的诸如聊天App中的缩略图等）。在线段树应用中，考虑成段修改，如果一定要每个元素都修改到位，显然时间复杂度不会低于$O(N)$。所以，必须不能修改到位，必须设置延迟标记。
关于延迟标记或者说$Lazy$标记：

1. 线段树的每个节点拥有一个延迟标记
2. 每个节点$t$的延迟标记实际上是为其子节点准备的
3. 每个节点$t$的延迟标记与其本身保存的内容（如区间和）没有直接关系

关于带延迟的修改操作，分两种情况，假设要修改的区间为$[a,b]$：

1. 如果线段树的节点$t$所对应的区间$[s,e]$是$[a,b]$的子区间，则设置延迟标记，不再往下修改
2. 否则，往下修改其子节点

例如在下图中，要求区间$[1,5]$中每个元素加100，则只需将根节点的$Lazy$标记设置为100即可。注意到：根节点的内容不再是1500，而是2000，这是修改以后的值。因此对于每一个节点而言，需要进行两类操作：与内容本身有关的操作，与延迟有关的操作。将1500修改为2000，这是第一类操作；将延迟标记加100，这是第二类操作。从这里也可以看出，根节点的信息是完全正确的，其子孙节点的信息是不正确的。因此根节点的延迟标记不是为根节点本身准备的，而是为其子孙节点准备的。

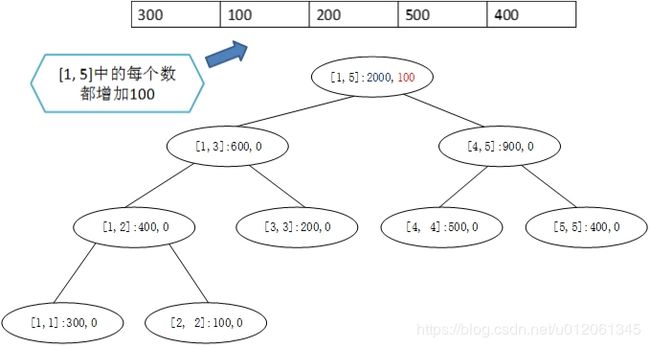
又如下例中，假设$[1,4]$加100，则根节点需要继续往下。对左边而言，到了左子节点$[1,3]$就可以停止了，设置好延迟标记就不用再往下了。对于右边而言，则需要一直往下，直到$[4,4]$为止。此时可以发现$[1,3]$以下的信息是不正确的，本次操作并没有修改到这些本应该修改的节点。

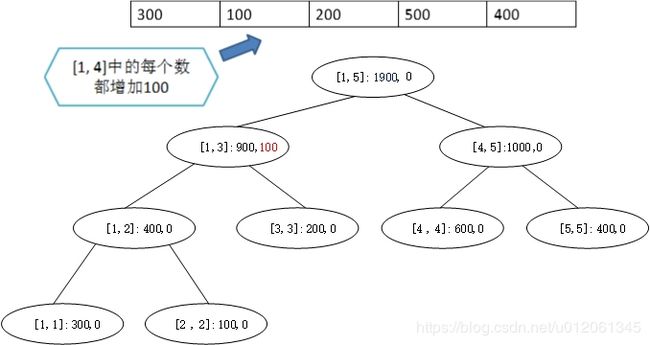
从上文的例子可以看出有些节点得信息是不正确的，如果此时需要查询与这些节点有关的信息该如何操作呢？很简单，在查询之前，首先结合父节点的延迟标记计算出正确信息即可。
例如在第一个例子中，如果需要查询区间$[1,3]$，根据递归调用的顺序，肯定首先到达的是根节点$[1,5]$，此时发现还需要往下递归，于是首先根据延迟标记计算出子节点正确的信息，再进入子节点即可。此时的线段树变成了如下所示：

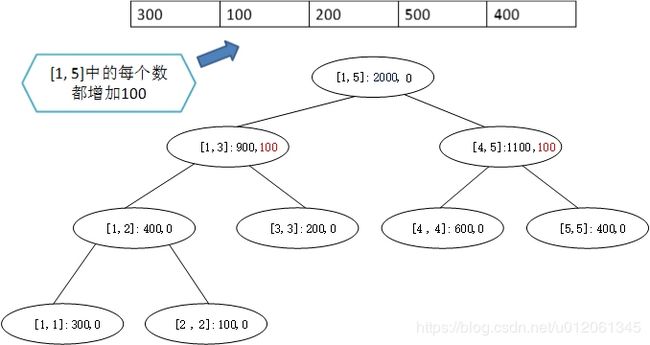
这里仍然体现了延迟操作的思想，查询到$[1,3]$，于是$[1,3]$节点的信息被正确的计算与保存，但是其下的子节点的信息仍然没有进行修改。不切实操作的节点，其信息就不会修改。这个操作既包含了修改也包含查询。

延迟操作代码实现

首先使用一个平行数组，为每一个节点记录上$Lazy$标记，然后写一个辅助函数，用于根据父节点的延迟信息，计算子节点的正确信息。

int Lazy[SIZE<<2];
//t表示当前节点，该函数用于计算t的子节点的正确信息
void _pushDown(int t, int s, int e){
    if( 0 == Lazy[t] ) return;
 
    int& lazy = Lazy[t];
    int m = ( s + e ) >> 1;
 
    int son = lson(t);
    ST[son] += lazy * ( m – s + 1 );//与内容有关的操作
    Lazy[son] += lazy;              //与延迟有关的操作

    son = rson(t);
    ST[son] += lazy * ( e – m );
    Lazy[son] += lazy;

    lazy = 0;
}

注意到本函数中主要实现的操作仍然包括两类：与内容本身有关的操作，与延迟有关的操作。
再考虑查询操作，对于带延迟操作的数据结构，其关键之一就是需要懂得在正确的地方执行延迟操作，如下：

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//[a, b]表示要查询的区间，注意在这一系列递归中[a, b]始终保持不变
int query(int t, int s, int e, int a, int b){
    if( a <= s && e <= b ){
        return ST[t];
    }

    _pushDown(t, s, e); //在正确的地方执行_pushDown即可
    int m = ( s + e ) >> 1;
    int ret = 0;
    if( a <= m ) ret += query(lson(t),s,m,a,b);
    if( m < b ) ret += query(rson(t),m+1,e,a,b); 
    return ret;
}

成段修改操作与单点修改操作的递归结束条件不同（其实单点修改的递归结束条件可以修改成与成段操作一模一样的形式，不过没有必要）。成段修改操作的递归结束条件与查询保持一致，因为这两个操作均是区间操作。

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//该操作表示将源数组[a, b]区间内所有元素值均增加delta
void modify(int t,int s,int e,int a,int b,int delta){
    if( a <= s && e <= b ){
        ST[t] += delta * ( e – s + 1 ); //与内容有关的操作
        Lazy[t] += delta;               //与延迟有关的操作
        return;
    }

    _pushDown(t, s, e);
    int m = ( s + e ) >> 1;
    if( a <= m ) modify(lson(t),s,m,a,b,delta);
    if( m < b ) modify(rson(t),m+1,e,a,b,delta); 
    _pushUp(t);
}

如果是不同修改类型，则需要将$pushDown$与$modify$函数做相应的修改。例如$set$修改操作的$modify$函数是（注意$pushDown$也要做修改）：

//t表示线段树节点，[s, e]表示该节点对应的源数组区间
//该操作表示将源数组[a, b]区间内所有元素值均设置为newValue
void modify(int t,int s,int e,int a,int b,int newValue){
    if( a <= s && e <= b ){
        ST[t] = newValue * ( e – s + 1 ); //与内容有关的操作
        Lazy[t] = newValue;               //与延迟有关的操作
        return;
    }

    _pushDown(t, s, e);
    int m = ( s + e ) >> 1;
    if( a <= m ) modify(lson(t),s,m,a,b,delta);
    if( m < b ) modify(rson(t),m+1,e,a,b,delta); 
    _pushUp(t);
}

多种延迟标记联合处理

假设题目需要实现多种不同的成段修改操作，则需要分别设置$Lazy$标记并且合理安排其处理的流程。考虑题目需要同时支持区间增量与区间设置操作，再假设查询操作是区间求和，则：

int LazyN[SIZE<<2];//区间设置操作的Lazy标记
int LazyD[SIZE<<2];//区间增量操作的Lazy标记

void _pushDown(int t, int s, int e){
    if(LazyN[t]){//先执行设置的延迟操作
        int&lazy = LazyN[t];
        int m = (s+e)>>1;
        int son = lson(t);
        ST[son] = lazy * (m-s+1);
        LazyN[son] = lazy;
        LazyD[son] = 0; //注意这一步
        son = rson(t);
        ST[son] = lazy * (e-m);
        LazyN[son] = lazy;
        LazyD[son] = 0;
        lazy = 0;
    }
    if(LazyD[t]){//再考虑增量的延迟操作
        int&lazy = LazyD[t];
        int m = (s+e)>>1;
        int son = lson(t);
        ST[son] += lazy * (m-s+1);
        LazyD[son] += lazy;
        son = rson(t);
        ST[son] += lazy * (e-m);
        LazyD[son] += lazy;
        lazy = 0;
    }
}

对于不同的修改操作，可以编写不同的$modify$函数进行实现，也可以在一个函数中实现，其实就是递归结束条件里面的代码不同而已，在递归那一块完全一样。

//将源数组[a,b]区间中所有的数设置成newValue
void modifyN(int t,int s,int e,int a,int b,int newValue){
    if( a <= s && e <= b ){
        ST[t] = newValue * ( e – s + 1 );
        LazyN[t] = newValue;
        LazyD[t] = 0;
        return;
    }

    _pushDown(t, s, e);
    int m = ( s + e ) >> 1;
    if( a <= m ) modifyN(lson(t),s,m,a,b, newValue);
    if( m < b ) modifyN(rson(t),m+1,e,a,b, newValue); 
    _pushUp(t);
}

//将源数组[a,b]区间中所有的数增加delta
void modifyD(int t,int s,int e,int a,int b,int delta){
    if( a <= s && e <= b ){
        ST[t] += delta * ( e – s + 1 );
        LazyD[t] += delta;
        return;
    }

    _pushDown(t, s, e);
    int m = ( s + e ) >> 1;
    if( a <= m ) modifyD(lson(t),s,m,a,b,delta);
    if( m < b ) modifyD(rson(t),m+1,e,a,b,delta); 
    _pushUp(t);
}

可以看到两个$modify$函数只在$if$语句内有所不同，之后的递归调用处的实现形式完全保持一致。而$if$语句里的处理又与$pushDown$函数中的操作存在一定的对应关系。在此基础上，可以使用线段树支持另外一些区间修改操作与查询操作。
例如大视野在线测评5039，要求支持三种操作：区间倍乘，区间增量，区间求和。hdu4578（AC代码）要求支持六种操作，三种查询、三种修改，分别是：区间倍乘，区间增量，区间设置，区间和，区间平方和，区间立方和。

区间合并问题与离散化

区间合并问题

除了常规的区间和、区间最值问题之外，还有一类称之为“区间合并”的问题（这只是一种习惯的称法）。典型的题目例如POJ2528（AC代码）：在数轴上一次给一段图上颜色，后面的颜色会覆盖前面的颜色，问最后能看到多少不同的颜色。类似这种有限状态的设置操作，并且查询的是跟连续段有关的信息，统称为区间合并问题，与最基本的区间和等区间问题在实现上还是有所区别。
但是其最基本的实现思路还是分治的思想，对于线段树每个节点所需要维护的区间信息，如果在已知左右子区间信息的情况下，可以快速的计算出父节点信息，则该问题就可以使用线段树完成。例如考虑POJ2528，令线段树节点保存3个信息（不包括延迟标记）：区间内连续的段数，左边界颜色，右边界颜色。是否能够根据左右子节点的这三种信息快速推出父节点的这三种信息？答案当然是肯定的，因此可以使用线段树。当然，这些信息还需要对回答问题有所帮助才行。
再例如POJ3667（AC代码），支持2种操作：

1. 1 $a$：找一段空间有连续$a$个空，分配出去，要求找到满足条件的最左边的连续空位
2. 2 $a$ $b$：从$a$开始的$b$个位置回收

对每个区间保存4种信息：该区间内最长可用空间，最长可用空间的起点，该区间左边界开始连续空位的长度，该区间右边界从右往左连续空位的长度。这4个信息，既能在$O(1)$时间内完成合操作，又能对回答问题有所帮助。因此完全可以使用线段树来进行解答。

离散化

离散化的基本想法

离散化通常伴随着区间合并操作出现。当然，也有典型的线段树需要实现离散化操作的题目。仍然考虑刚才的POJ2528，该题目的数轴长度是1千万，而操作总数是1万个。显然不可能将这1千万的长度做成线段树。离散化操作其本质就是一种操作的映射，将原题的操作映射为离散化以后的操作，且映射前后保持某种不变性（针对具体查询的不变性）。
离散化的基本示例：假设依次有以下区间操作：

1. 第一个操作把[1,1亿]之间的数都设置成1
2. 第二个操作把[5,2亿]之间的数都设置成2
3. 第三个操作问[9,1亿2]的最小值是多少

将操作出现的数进行排序，依次为$[1,5,9,1亿,1亿2,2亿]$，因此分别映射为$[1,2,3,4,5,6]$，则原操作变为：

1. 第一个操作把[1, 4]之间的数都设置成1
2. 第二个操作把[2, 6]之间的数都设置成2
3. 第三个操作问[3, 5]的最小值是多少

此时发现查询操作的结果是一致的。

离散化的陷阱

离散化存在一些陷阱。仍然是刚才的例子，将参数改为：

1. [60, 90]设置成1
2. [30, 60]设置成2
3. [90, 130]设置成2
4. [60, 90]的最小值是多少

将$[30,60,90,130]$分别映射为$[1,2,3,4]$，则操作变为：

1. [2, 3]设置成1
2. [1, 2]设置成2
3. [3, 4]设置成2
4. [3, 4]的最小值是多少

这个离散化是不正确。因为它将某些区域的信息给掩盖了。解决这一问题的一个方法是插值，即在给定参数的两边均参与离散化。对于上例就是将$[29,30,31,59,60,61,89,90,91,129,130,131]$参与离散化，分别得到$[1,2,3,4,5,6,7,8,9,10,11,12]$，则操作变为：

1. [5, 8]设置成1
2. [1, 5]设置成2
3. [8 11]设置成2
4. [5, 8]的最小值是多少

此时可得到正确答案。
还有一类问题也存在离散化的陷阱，但解决办法要容易一些，这就是有关数轴的区间问题。仍然是POJ2528。假设存在如下操作：

1. [6, 9]设置成红色
2. [3, 6]设置成蓝色
3. [9, 13]设置成蓝色

简单离散化以后，发现区间全部变成了蓝色，本来应该是“蓝红蓝”。这个原因与上一个例子是一样的，也是由于不正确的离散化掩盖了某些区间的信息。这个问题也可以通过插值解决，不过还有一种更简单的方法。数轴涂色其实与数组涂色有一点点区别。考虑给数轴的$[1,3]$涂色，其实并不是给3个点进行涂色，而是给2个格进行涂色（$[1,2]$是一格，$[2,3]$是一格）。这个关键的区别在于：如果是点涂色，则[1,3]涂色，再[3, 4]涂色，此时点3被涂了两遍，前面的颜色被覆盖了。而数轴涂色，同样的操作，并无任何颜色被覆盖。因此数轴涂色实际上可以解释为一个左闭右开的区间操作，数轴上的$[1,3]$涂色其实可以解释为$[1,3)$的点涂色，即将$[1,2]$的2个格子涂色。所以对于数轴涂色而言，只需把离散化以后的右边界减1即可。想象一下，数轴涂色绝对不可能存在$[1,1]$的原始操作，至少也是$[1,2]$。上例中，将$[3,6,9,13]$离散化为$[1,2,3,4]$，则操作变为：

1. [2, 3)设置成红色，其实是[2,2]设置成红色
2. [1, 2)设置成蓝色，其实是[1,1]设置成蓝色
3. [3, 4)设置成蓝色，其实是[3,3]设置成蓝色

离散化的实现

离散化的实现其实比较简单，因为无论怎么折腾其理论时间复杂程度不会降低。因此不需要太多的代码设计，直接排序unique再加二分查找即可。

//假设T数组内保存了原操作所涉及到的索引参数数据，且有效长度为NN，从0开始编号
int T[];
//对其排序并unique
sort(T, T+NN);
NN = unique(T, T+NN) - T;

这样处理以后，再在线段树操作之前，做一个二分查找即可。

//对每一个操作
//假设Ai和Bi是该操作的原始参数，做一个二分查找
int a = lower_bound(T,T+NN,A[i]) - T + 1;
int b = lower_bound(T,T+NN,B[i]) - T + 1;
//在线段树上以a,b作为参数进行操作
modify(1,1,N,a,b,...);

扫描线

扫描线是计算几何的一种思想，通过依次处理扫描线事件来达到某种目的。不过有一类扫描线问题可以借助线段树来进行维护，这就是hdu1542矩形并求面积和hdu1828矩形并求周长。
这一类问题中的线段树使用又不同于上面的一些例子。此类问题当然也属于区间合并问题，但是只需支持两种状态即可，即进入矩形时的设置操作（或者称为置1操作）与离开矩形的清除操作（或者称为清0操作），另外最关键的是：置1操作与清0操作一定是成对出现的，操作的区间一定是一模一样的。正是这个特点使得扫描线里的线段树与上述线段树的操作有一些显著的不同。

总结

本质上而言，线段树是对区间问题实现分治策略的一种代码模板。对于大众化的或者已经广为人知的区间问题，基本的框架都是固定的，只需考虑几个实现细节即可，诸如：$pushUp$，$pushDown$，$modify$的递归结束条件里的实现细节等等。而对于更一般的问题，从基本的分治思想入手构建线段树，再加以一定的优化，可能是更有效的思维模式。