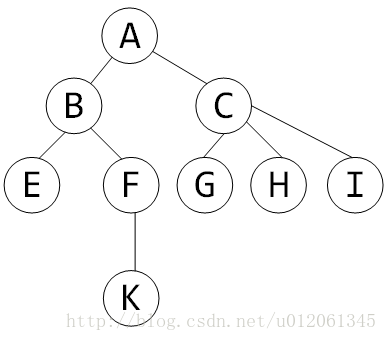
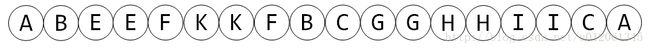树的DFS序

树是一种非线性结构，一般而言，我们总是想办法将其转化为线性结构，将树上操作包括子树操作、路径操作等转化为数组上的区间操作，从而在一个较为理想的复杂度内加以解决。将树“拍平”的方法有很多，例如欧拉序、HLD等。实际上欧拉序也是在DFS过程中得到的。不过通常而言，我们所说的DFS序是指：每个节点进出栈的时间序列。

考虑上图中树的DFS序，应为

其中，每个节点均会出现2次，第一次是进入DFS的时刻，第二次是离开DFS的时刻。分别称之为 In 与 Out 。在区间操作中，如果某个节点出现了2次，则该节点将被“抵消”。所以通常会将 Out 时刻对应的点设置为负数。

树的DFS序列有几个有用的性质：

1. 任意子树是连续的。例如子树 BEFK ，在序列中对应 BEEFKKFB ；子树 CGHI ，在序列中对应连续区间 CGGHHIIC 。
2. 任意点对 (a,b) 之间的路径，可分为2种情况，首先令 lca 是 a 、 b 的最近公共祖先：
   
   1. 若 lca 是 a 、 b 之一，则 a 、 b 之间的 In 时刻的区间或者 Out 时刻区间就是其路径。例如 AK 之间的路径就对应区间 ABEEFK ，或者 KFBCGGHHIICA 。
   2. 若 lca 另有其人，则 a 、 b 之间的路径为 In[a] 、 Out[b] 之间的区间或者 In[b] 、 Out[a] 之间的区间。另外，还需额外加上 lca ！！！考虑 EK 路径，对应为 EFK 再加上 B 。考虑 EH 之间的路径，对应为 EFKKFBCGGH 再加上 A 。

利用这些性质，可以利用DFS序列完成子树操作和路径操作，同时也有可能将莫队算法应用到树上从而得到树上莫队。

BZOJ4034需要在树上完成3类操作，单点更新，子树更新，以及根到指定节点的路径查询。利用性质1以及性质2.1即可完成，连 LCA 都无需求出。对整个DFS序列使用线段树进行维护，注意到整个序列实际上有正有负，因此额外用一个域来表示正数的个数。

#include 
#include 
#include 
using namespace std;

int const SIZE = 100100;
typedef long long weight_t;

struct edge_t{
    int to;
    int next;
}Edge[SIZE<<1];
int Vertex[SIZE];
int ECnt;
weight_t W[SIZE];

inline void mkEdge(int a,int b){
    Edge[ECnt].to = b;
    Edge[ECnt].next = Vertex[a];
    Vertex[a] = ECnt++;

    Edge[ECnt].to = a;
    Edge[ECnt].next = Vertex[b];
    Vertex[b] = ECnt++;
}

int InIdx[SIZE],OutIdx[SIZE];
int InOut[SIZE<<1];
int NewIdx[SIZE<<1];
int NCnt;

void dfs(int node,int parent){
    NewIdx[NCnt] = node;
    InOut[NCnt] = 1;
    InIdx[node] = NCnt++;
    for(int next=Vertex[node];next;next=Edge[next].next){
        int son = Edge[next].to;
        if ( son != parent ) dfs(son,node);
    }
    NewIdx[NCnt] = node;
    InOut[NCnt] = -1;
    OutIdx[node] = NCnt++;
}

int N;
weight_t StSum[SIZE<<3];
weight_t Lazy[SIZE<<3];
int Flag[SIZE<<3];//The count of the positive number in the range

inline int lson(int x){return x<<1;}
inline int rson(int x){return lson(x)|1;}

inline void _pushUp(int t){
    StSum[t] = StSum[lson(t)] + StSum[rson(t)];
    Flag[t] = Flag[lson(t)] + Flag[rson(t)];
}

inline void _pushDown(int t){
    if ( 0LL == Lazy[t] ) return;

    weight_t& x = Lazy[t];

    int son = lson(t);
    StSum[son] += Flag[son] * x;
    Lazy[son] += x;

    son = rson(t);
    StSum[son] += Flag[son] * x;
    Lazy[son] += x;

    x = 0LL;
}

void build(int t,int s,int e){
    Lazy[t] = 0LL;
    if ( s == e ){
        StSum[t] = InOut[s] * W[NewIdx[s]];
        Flag[t] = InOut[s];
        return;
    }

    int m = ( s + e ) >> 1;
    build(lson(t),s,m);
    build(rson(t),m+1,e);
    _pushUp(t);
}

void modify(int t,int s,int e,int a,int b,weight_t delta){
    if ( a <= s && e <= b ){
        StSum[t] += Flag[t] * delta;
        Lazy[t] += delta;
        return;
    }

    _pushDown(t);
    int m = ( s + e ) >> 1;
    if ( a <= m ) modify(lson(t),s,m,a,b,delta);
    if ( m < b ) modify(rson(t),m+1,e,a,b,delta);
    _pushUp(t);
}

weight_t query(int t,int s,int e,int a,int b){
    if ( a <= s && e <= b ){
        return StSum[t];
    }

    _pushDown(t);

    weight_t ret = 0LL;
    int m = ( s + e ) >> 1;
    if ( a <= m ) ret += query(lson(t),s,m,a,b);
    if ( m < b ) ret += query(rson(t),m+1,e,a,b);
    return ret;
}

inline weight_t query(int x){
    return query(1,1,N<<1,1,InIdx[x]);
}

inline void modify(int x,weight_t delta){
    modify(1,1,N<<1,InIdx[x],InIdx[x],delta);
    modify(1,1,N<<1,OutIdx[x],OutIdx[x],delta);
}

inline void modifySubtree(int x,weight_t delta){
    modify(1,1,N<<1,InIdx[x],OutIdx[x],delta);
}

inline void initTree(int n){
    ECnt = NCnt = 1;
    fill(Vertex,Vertex+n+1,0);
}

int M;
bool read(){
    if ( EOF == scanf("%d%d",&N,&M) ) return false;

    initTree(N);
    for(int i=1;i<=N;++i)scanf("%lld",W+i);

    int a,b;
    for(int i=1;iscanf("%d%d",&a,&b);
        mkEdge(a,b);
    }

    dfs(1,0);
    build(1,1,N<<1);
    return true;
}

void proc(){
    int cmd,x;
    weight_t a;
    while(M--){
        scanf("%d%d",&cmd,&x);
        switch(cmd){
        case 1:scanf("%lld",&a);modify(x,a);break;
        case 2:scanf("%lld",&a);modifySubtree(x,a);break;
        case 3:printf("%lld\n",query(x));break;
        }
    }
}
int main(){
    //freopen("1.txt","r",stdin);
    while( read() ) proc();
    return 0;
}