动态规划：求最长公共子串/最长公共子序列

最长公共子序列和最长公共子串区别

       最长公共子串（Longest Common Substring）与最长公共子序列（Longest Common Subsequence）的区别： 子串要求在原字符串中是连续的，而子序列则只需保持相对顺序一致，并不要求连续。例如X = {a, Q, 1, 1}; Y = {a, 1, 1, d, f}那么，{a, 1, 1}是X和Y的最长公共子序列，但不是它们的最长公共字串。

一、最长公共子序列

具体的算法思想参考以下文章：

http://blog.csdn.net/lisonglisonglisong/article/details/41548557

http://blog.csdn.net/zhongkeli/article/details/8847694

只求最长子序列长度

如果仅仅需要知道最长子序列的长度值，代码如下：

#include 
#include 
#include 
#include 
#include 
using namespace std;

//最长公共子串（LCS）
//二维数组veca记录的是两个字符串Xi和Yj的LCS长度
int LCS_length(const string &str1, const string &str2, vector > &veca) {
	int i, j;
	int biggest = 0;
	if (str1 == "" || str2 == "")
		return 0;

	for (i = 0; i <= str1.length(); i++) {
		veca[i][0] = 0;
	}
	for (j = 0; j <= str2.length(); j++) {
		veca[0][j] = 0;
	}
	for (i = 1; i <= str1.length(); i++) {
		for (j = 1; j <= str2.length(); j++) {
			if (str1[i - 1] == str2[j - 1]) {
				veca[i][j] = veca[i - 1][j - 1] + 1;
			}
			else {
				if (veca[i - 1][j] >= veca[i][j - 1])
					veca[i][j] = veca[i - 1][j];
				else
					veca[i][j] = veca[i][j-1];
			}
		}
	}
	return veca[str1.length()][str2.length()];
}

int main() {
	string input;
	getline(cin, input);
        stringstream ss(input);
        string str1, str2;
	ss >> str1;
	ss >> str2;
	//将veca初始化为一个二维数组,其行列值分别为str1和str2的长度加1
	//二维数组veca记录的是两个字符串Xi和Yj的LCS长度
	vector > veca(str1.length() + 1, vector(str2.length() + 1));
	cout << LCS_length(str1, str2, veca) << endl;
	return 0;
}

结果：

动态规划解决LCS问题的时间复杂度为 O(mn)，这比简单的递归实现要快多了。空间复杂度是O(mn)，因为使用了一个动态规划表。

要输出一个LCS的内容

和上面的程序比，只需要多一个二维数组记录在遍历中所选择的子问题的最优解即可。如下程序：

//输出最长公共子串（LCS）
//二维数组veca记录的是两个字符串Xi和Yj的LCS长度
int LCS_length(const string &str1, const string &str2, 
	            vector > &veca, vector > &vecb) {
	int i, j;
	int biggest = 0;
	if (str1 == "" || str2 == "")
		return 0;

	for (i = 0; i <= str1.length(); i++) {
		veca[i][0] = 0;
	}
	for (j = 0; j <= str2.length(); j++) {
		veca[0][j] = 0;
	}
	for (i = 1; i <= str1.length(); i++) {
		for (j = 1; j <= str2.length(); j++) {
			//如果Xi-1 == Yj-1，那么最长子序列为veca[i - 1][j - 1] + 1
			//此时将vecb[i][j] = 1表明str1[i-1]是子问题LCS的一个元素
			if (str1[i - 1] == str2[j - 1]) {
				veca[i][j] = veca[i - 1][j - 1] + 1;
				vecb[i][j] = 1;
			}
			else {
				if (veca[i - 1][j] >= veca[i][j - 1]) {
					veca[i][j] = veca[i - 1][j];
					vecb[i][j] = 2;
				}
				else {
					veca[i][j] = veca[i][j-1];
					vecb[i][j] = 3;
				}
			}
		}
	}
	return veca[str1.length()][str2.length()];
}

//该函数用于输出一个LCS的序列
//这里输出的顺序是先向上寻找，再向左寻找
void PrintOneLCS(vector > &vecb, string &str1, int i, int j) {
	if (i == 0 || j == 0)
		return;
	if (vecb[i][j] == 1) {
		PrintOneLCS(vecb, str1, i - 1, j - 1);
		cout << str1[i - 1] << " ";
	}
	else if (vecb[i][j] == 2)
		PrintOneLCS(vecb, str1, i -1, j);
	else
		PrintOneLCS(vecb, str1, i, j - 1);
}

int main() {
	string input;
	getline(cin, input);
	stringstream ss(input);
	string str1, str2;
	ss >> str1;
	ss >> str2;
	//将veca初始化为一个二维数组,其行列值分别为str1和str2的长度加1
	//二维数组veca记录的是两个字符串Xi和Yj的LCS长度
	//二维数组vecb[i][j]记录veca[i][j]时所选择的子问题的最优解
	vector > veca(str1.length() + 1, vector(str2.length() + 1));
	vector > vecb(str1.length() + 1, vector(str2.length() + 1));
	cout << LCS_length(str1, str2, veca, vecb) << endl;
	PrintOneLCS(vecb, str1, str1.length(), str2.length());
	return 0;
}

求一个LCS内容也可以不借助辅助二维数组vecb而是用下面小节的方法，

//该函数用于输出一个LCS的序列，使用下一小节的方法
//这里输出的顺序是先向左寻找，再向上寻找
void PrintOneLCS(string &str1, string &str2, int i, int j, 
	vector > &veca) {
		string lcs_str;
		while (i > 0 && j > 0) {
			if (str1[i - 1] == str2[j - 1]) {
				lcs_str = str1[i - 1] + lcs_str;
				--i;
				--j;
			}
			else {
				//如果左边存在LCS就从左边找否则再从右边找
				if (veca[i - 1][j] >= veca[i][j - 1])
					--i;
				else
					--j;
			}
		}
		cout << lcs_str << endl;
}

如下代码：

要输出所有LCS的内容

两个字符串对应的最长公共子序列不一定唯一，这个程序输出所有的LCS内容。

基本思想是：

具体参考文章：http://blog.csdn.net/lisonglisonglisong/article/details/41596309

代码：

#include 
#include 
#include 
#include 
#include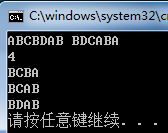 

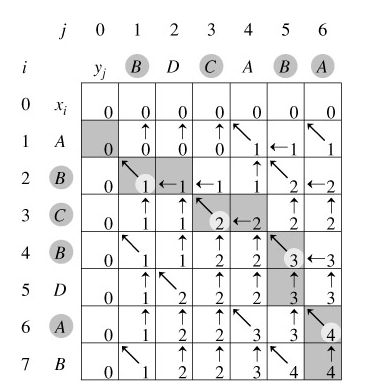
如图所示的两个字符串共有三个LCS。

二、最长公共子串

描述：

计算两个字符串的最大公共子串（Longest Common Substring）的长度，字符不区分大小写。

输入：

输入两个字符串

输出：

输出一个整数

样例输入：

asdfas werasdfaswer

样例输出：

6

这里的最大公共字串要求的字串是连续的。

求字串的方法和求子序列方法类似：

当str1[i] == str2[j]时，子序列长度veca[i][j] = veca[i - 1][j - 1] + 1；只是当str1[i] ！= str2[j]时，veca[i][j]长度要为0，而不是max{veca[i - 1][j], veca[i][j - 1]}。

    #include   
    #include   
    #include   
    #include   
    #include   
    using namespace std;  
      
    int LCS_length(const string &str1, const string &str2, vector > &veca) {  
        int i, j;  
        int biggest = 0;  
        if (str1 == "" || str2 == "")  
            return 0;  
        for (i = 0; i <= str1.length(); i++) {  
            veca[i].resize(str2.length() + 1, 0);  
        }  
        for (j = 0; j <= str2.length(); j++) {  
            veca[0][j] = 0;  
        }  
        for (i = 1; i <= str1.length(); i++) {  
            for (j = 1; j <= str2.length(); j++) {  
                if (str1[i - 1] == str2[j - 1]) {  
                    veca[i][j] = veca[i - 1][j - 1] + 1;  
                    if (veca[i][j] > biggest)  
                        biggest = veca[i][j];  
                }  
                else  
       //可以看出，求最长子串和求最长子序列差别仅仅在这里
                    veca[i][j] = 0;  
                  
            }  
        }  
        return biggest;  
    }  
      
    int main() {  
        string input;  
        getline(cin, input);  
        stringstream ss(input);  
        string str1;  
        ss >> str1;  
        string str2;  
        ss >> str2;  
        vector > veca(str1.length() + 1);  
        cout << LCS_length(str1, str2, veca) << endl;  
        return 0;  
    }  

同样适用求最长子序列的测试数据，得到它们的公共最长子串长度为2，而它们的公共最长子序列长度为4.

三、动态规划的其它题目

1、硬币面值组合问题

http://www.cnblogs.com/python27/archive/2013/09/05/3303721.html

2、最长递增子序列

           除了动态规划，该题还有其他解法。

3、数组最大子数组和的最大值

http://www.ahathinking.com/archives/120.html

3、动态规划之钢条分割

4、计算两个字符串的相似度（编程之美）

       该文章原理说得比较清楚： 点击打开链接

       这里是代码： 点击打开链接

5、求每一对顶点之间的最短路径：Floyd-Warshall算法