matlab利用fsolve函数研究异步电动机的特性

fsolve函数

对于非线性方程的求根问题，Matlab软件开发了基于最小二乘法来解其根的函数。位于优化工具箱（Optimization Toolbox）内。求解非线性方程组F(X)=0,用fsolve函数的调用格式为X=fsolve(@fun,X0,option)，其中：
X为返回的解；
fun是用于定于需求解的非线性方程组的函数文件名;
X0是求根过程的初值;
option为最优化工具箱的选项设定。
优化工具箱提供了20个选项，用户可以使用optimset命令将它们显示出来。如果改变其中的某个选项，则可以调用optimset函数来完成。例如：
optimset(‘Display’,‘off/iter/final’)。

应用举例

求下列非线性方程组在（0.5,0.5）附近的数值解。

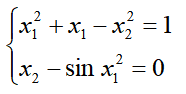
步骤如下：
（1）建立函数文件myfun.m

function q=myfun(p)
x1=p(1);
x2=p(2);
q(1)=x1^2+x1-x2^2-1;
q(2)=x2-sin(x1^2);

（2）在给定的初值（0.5,0.5）下，调用fsolve函数求方程的根。

function q=myfun(p)
x=fsolve(@myfun,[0.5,0.5],optimset('Display','off'))

解的结果如下：
x=0.7260
0.5029

电机特性研究

转矩特性：当输入电压U1和频率f1一定，且电机参数不变时，异步电动机转矩T与转差率s的关系式T=f(s)称为转矩特性。
$$T=C_T{U}_1^2\frac{s{R}_2}{R_2^2+(s{X}_{2}0){)}^2}.$$
机械特性：异步电动机的转速n与转矩T之间的关系n=f(T)称为机械特性。将转差率$$s_N=\frac{n_1-n}{n_1}.$$代入转矩特性公式，即可得到转速与转矩的关系。

例题

解：（1~4）问基本运算

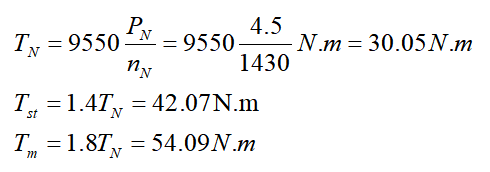
可以看出，该异步电动机不论其在星形联结（线电压380V）还是三角形联结（线电压220V）的情况下，其产生的电磁转矩是一样的。

解：（5）转矩特性和机械特性

转换为以下问题

编写非线性方程组函数程序myfun.m

function q=myfun(p)
ct=p(1);
r2=p(2);
x2=p(3);
q(1)=ct*380^2/(2*x2)-54.07;
q(2)=ct*380^2*r2/(r2^2+x2^2)-42.07;
q(3)=ct*380^2*0.04667*r2/(r2^2+(0.04667*x2)^2)-30.05;

命令提示行输入代码：

x=fsolve(@myfun,[1,1,1],optimset('Display','off'))

运行结果：
x =

0.0059    4.5763    7.8990

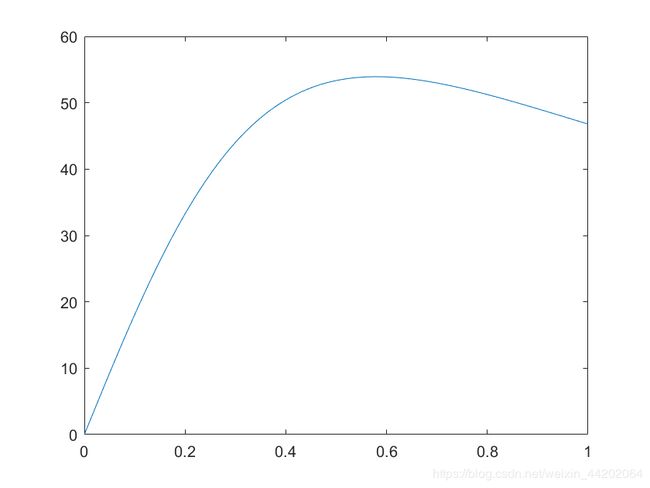
转矩特性的绘制

s=0:0.01:1；
 t=0.0059*380^2*s*4.5763./(4.5763^2+(s*7.899).^2);
 plot(s,t)

机械特性的绘制

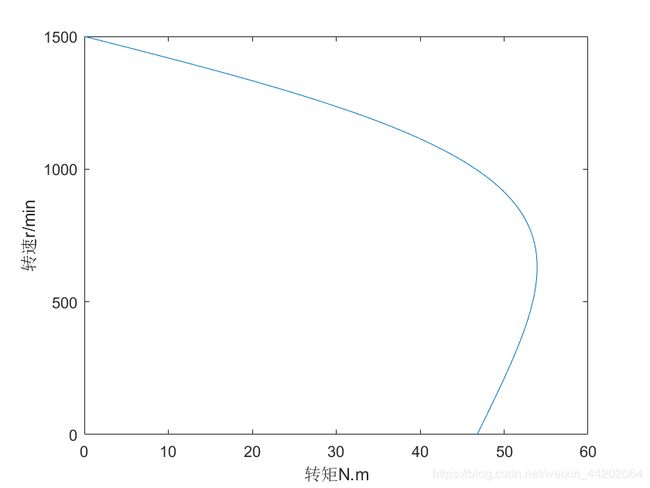
 nN=1500;
 s=(nN-n)/nN;
 t=0.0059*380^2*s.*4.5763/(4.5763^2+(s*7.899).^2);
 plot(t,n)
 t=0.0059*380^2*s.*4.5763./(4.5763^2+(s*7.899).^2);
 plot(t,n)
 xlabel('转矩N.m')
 ylabel('转速r/min')

运行结果：