防爆秃击队——线段树/树状数组/cdq分治专题训练(一)
A - 敌兵布阵(hdu 1166)
1.题目描述:
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4)End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Sample Output
Case 1:
6
33
59
2.题意:
中文,略。
3.思路:
树状数组/线段树的模板题。因为没有区间修改,所以比较建议树状数组。
4.代码:
//A - 敌兵布阵
#includeB - I Hate It(HDU - 1754)
1.题目描述:
很多学校流行一种比较的习惯。老师们很喜欢询问,从某某到某某当中,分数最高的是多少。
这让很多学生很反感。
不管你喜不喜欢,现在需要你做的是,就是按照老师的要求,写一个程序,模拟老师的询问。当然,老师有时候需要更新某位同学的成绩。
Input
本题目包含多组测试,请处理到文件结束。
在每个测试的第一行,有两个正整数 N 和 M ( 0
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取’Q’或’U’) ,和两个正整数A,B。
当C为’Q’的时候,表示这是一条询问操作,它询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少。
当C为’U’的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
Output
对于每一次询问操作,在一行里面输出最高成绩。
Sample Input
5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5
Sample Output
5
6
5
9
Hint
Huge input,the C function scanf() will work better than cin
2.题意:
略
3.思路:
和A类似,点修区查。所以比较推荐树状数组,线段树也可以。树状数组要注意的点是原数组不能省,因为对比极值的时候需要,而且树状数组的时间复杂度是查询和修改都是O(log2n),但是空间是O(n)的。下图可供对比:![]()
4.代码:
//B - I Hate It
#include树状数组做法:
//B - I Hate It
#includeC - Just a Hook(HDU_1698)
1.题目描述:
In the game of DotA, Pudge’s meat hook is actually the most horrible thing for most of the heroes. The hook is made up of several consecutive metallic sticks which are of the same length.
Now Pudge wants to do some operations on the hook.
Let us number the consecutive metallic sticks of the hook from 1 to N. For each operation, Pudge can change the consecutive metallic sticks, numbered from X to Y, into cupreous sticks, silver sticks or golden sticks.
The total value of the hook is calculated as the sum of values of N metallic sticks. More precisely, the value for each kind of stick is calculated as follows:
For each cupreous stick, the value is 1.
For each silver stick, the value is 2.
For each golden stick, the value is 3.
Pudge wants to know the total value of the hook after performing the operations.
You may consider the original hook is made up of cupreous sticks.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains an integer N, 1<=N<=100,000, which is the number of the sticks of Pudge’s meat hook and the second line contains an integer Q, 0<=Q<=100,000, which is the number of the operations.
Next Q lines, each line contains three integers X, Y, 1<=X<=Y<=N, Z, 1<=Z<=3, which defines an operation: change the sticks numbered from X to Y into the metal kind Z, where Z=1 represents the cupreous kind, Z=2 represents the silver kind and Z=3 represents the golden kind.
Output
For each case, print a number in a line representing the total value of the hook after the operations. Use the format in the example.
Sample Input
1
10
2
1 5 2
5 9 3
Sample Output
Case 1: The total value of the hook is 24.
2.题意:
给出一段区间[1,n],然后这段区间初始值都为1,现在指定一个区间[a,b],把它变成1,2,3其中一个数。最后输出整个区间的区间和。
3.思路:
因为有区修,所以还是推荐线段树(树状数组也可以,不过可能比较麻烦【说实话差不多23333】)。多Case问题,所以注意变量的初始化以及lazy标记的更新!
4.代码:
//C - Just a Hook
#includeD - Minimum Inversion Number(hdu1394)
1.题目描述:
The inversion number of a given number sequence a1, a2, …, an is the number of pairs (ai, aj) that satisfy i < j and ai > aj.
For a given sequence of numbers a1, a2, …, an, if we move the first m >= 0 numbers to the end of the seqence, we will obtain another sequence. There are totally n such sequences as the following:
a1, a2, …, an-1, an (where m = 0 - the initial seqence)
a2, a3, …, an, a1 (where m = 1)
a3, a4, …, an, a1, a2 (where m = 2)
…
an, a1, a2, …, an-1 (where m = n-1)
You are asked to write a program to find the minimum inversion number out of the above sequences.
Input
The input consists of a number of test cases. Each case consists of two lines: the first line contains a positive integer n (n <= 5000); the next line contains a permutation of the n integers from 0 to n-1.
Output
For each case, output the minimum inversion number on a single line.
Sample Input
10
1 3 6 9 0 8 5 7 4 2
Sample Output
16
2.题意:
求序列0到n-1某一排列的逆序数,但是并不只是如此,要求这个序列把a1放最后,把a2放最后……一直到把an-1放最后,这一组n个序列的逆序数的最小值。
3.思路:
开始有难度了233333,但是其实是一道数学题。假设我们求得本次序列的逆序数N,那么我们把开头放在尾部的逆序数变化是多少呢?首先,假设第一个元素值为 i ,那么后面比它小的总共有 0,1,2,…,i-1,总共 i 个,所以要减去它原来的贡献 i ,那么它放到最后呢,对于新的逆序数的贡献有 n-i-1。所以新的逆序数为:N - 2*i -1。与原来取min就可以了。 所以问题就转换为:如何求原始序列的逆序数。这里我用的方法是:cdq分治,推荐做法是:权值树状数组记录逆序数。(树状数组待补)
4.代码:
//D - Minimum Inversion Number
#includeE - Billboard(HDU 2795)
1.题目描述:
At the entrance to the university, there is a huge rectangular billboard of size h*w (h is its height and w is its width). The board is the place where all possible announcements are posted: nearest programming competitions, changes in the dining room menu, and other important information.
On September 1, the billboard was empty. One by one, the announcements started being put on the billboard.
Each announcement is a stripe of paper of unit height. More specifically, the i-th announcement is a rectangle of size 1 * wi.
When someone puts a new announcement on the billboard, she would always choose the topmost possible position for the announcement. Among all possible topmost positions she would always choose the leftmost one.
If there is no valid location for a new announcement, it is not put on the billboard (that’s why some programming contests have no participants from this university).
Given the sizes of the billboard and the announcements, your task is to find the numbers of rows in which the announcements are placed.
Input
There are multiple cases (no more than 40 cases).
The first line of the input file contains three integer numbers, h, w, and n (1 <= h,w <= 10^9; 1 <= n <= 200,000) - the dimensions of the billboard and the number of announcements.
Each of the next n lines contains an integer number wi (1 <= wi <= 10^9) - the width of i-th announcement.
Output
For each announcement (in the order they are given in the input file) output one number - the number of the row in which this announcement is placed. Rows are numbered from 1 to h, starting with the top row. If an announcement can’t be put on the billboard, output “-1” for this announcement.
Sample Input
3 5 5
2
4
3
3
3
Sample Output
1
2
1
3
-1
2.题意:
有一块高h,宽w的广告版,每次贴一块广告,高1,宽x,贴在最左上的位置,问每一个广告的行数,贴不了的话就输出-1。
3.思路:
这题要转换一下,线段树需要明确每个节点维护的是什么,以及我们的查询的是什么,修改的是什么。 因为是单位高度,我们可以横过来,把高度当成一个连续的区间,就可以转换为区间问题了。那么我们每个节点所代表的值就变成了:我们剩余的宽度。明确到这一步,下面我们就要想:我们查询什么东西?——大于等于宽度x的最左节点。那么我们维护当然不可以这样维护,那么我们可以分为两步:维护区间最大值,如果x的值小于区间最大值,则优先选择左子树(因为我们要最左),直到到达叶子节点为止。 代码注意的地方:因为数据范围h是1e9,但是n只要2e5左右,那么我们最多就分n个,所以我们选min(h,n)来建树,另外,查询修改的时候一定要update!所以不建议直接返回行数,不方便修改的更新。
4.代码:
//E - Billboard
#includeF - Tunnel Warfare (HDU 1540)
1.题目描述:
During the War of Resistance Against Japan, tunnel warfare was carried out extensively in the vast areas of north China Plain. Generally speaking, villages connected by tunnels lay in a line. Except the two at the ends, every village was directly connected with two neighboring ones.
Frequently the invaders launched attack on some of the villages and destroyed the parts of tunnels in them. The Eighth Route Army commanders requested the latest connection state of the tunnels and villages. If some villages are severely isolated, restoration of connection must be done immediately!
Input
The first line of the input contains two positive integers n and m (n, m ≤ 50,000) indicating the number of villages and events. Each of the next m lines describes an event.
There are three different events described in different format shown below:
D x: The x-th village was destroyed.
Q x: The Army commands requested the number of villages that x-th village was directly or indirectly connected with including itself.
R: The village destroyed last was rebuilt.
Output
Output the answer to each of the Army commanders’ request in order on a separate line.
Sample Input
7 9
D 3
D 6
D 5
Q 4
Q 5
R
Q 4
R
Q 4
Sample Output
1
0
2
4
2.题意:
给出一个区间[1,n],给出m个操作,分别为D x:摧毁,把x点变为不通;R:恢复,恢复上一个摧毁的点,使之连通(恢复过则顺位);Q x:查询,查询x点左右连通的点数。
3.思路:
(某大佬用树状数组+前后缀过了,并称之为“水题”。大佬的题解 orz)本人不会,参考了别的博主发现是:线段树+区间合并。思路是维护三个值:ls:从左节点 L 开始的可通点的数量;rs:以右节点为终点的可通点的数量;ms:区间最大可通点的数量。我们修改就是单点修改:点x连通与否。重点就是查询了:查询点x的最大连通点的数量。
因为这题不太好理解,所以我把代码两部分比较难的解析一下思路:
(一):更新操作:
我们维护的三个值如何更新父亲区间的值?
inline void update(int k)
{
t[k].ls=t[lc(k)].ls;
if(t[lc(k)].ls==t[lc(k)].r-t[lc(k)].l+1)
t[k].ls+=t[rc(k)].ls;
t[k].rs=t[rc(k)].rs;
if(t[rc(k)].rs==t[rc(k)].r-t[rc(k)].l+1)
t[k].rs+=t[lc(k)].rs;
t[k].ms=max(max(t[lc(k)].ms,t[rc(k)].ms),t[lc(k)].rs+t[rc(k)].ls);
}
首先,我们父亲区间假设节点为k。那么:
t[k].ls=t[2k].ls;父亲区间左节点开始的连通点一定是左子树的左节点开始的连通点。但是如果子树中间无间断点,那么t[k].ls+=t[2k+1].ls。即加上右子树的从左节点开始的连通点。(不懂就画个图就懂了)右节点同理。
但是对于区间最大连通点数,不可以直接是左右子树的最大值,因为有可能中间有一段是连通的,所以我们应该综合考虑:左子树的以右节点结尾的连续点数加上右子树以左节点开始的连续点数,左右子树的连通点数,这三者的最大值。
举个例子:(1 1 0 1)(1 1 1 0);左子树最大是3,右子树最大也是3,但是中间连通最大是4。
(二):查询操作
如何查询某一个点的最大连通点数?
int query(int x,int k=1)
{
if(t[k].l==t[k].r||!t[k].ms||t[k].ms==t[k].r-t[k].l+1)
return t[k].ms;
int m=(t[k].l+t[k].r)>>1;
if(x<=m)
{
if(x>=t[lc(k)].r-t[lc(k)].rs+1)
return query(x,lc(k))+query(m+1,rc(k));
else
return query(x,lc(k));
}
else
{
if(x<=t[rc(k)].l+t[rc(k)].ls-1)
return query(x,rc(k))+query(m,lc(k));
else
return query(x,rc(k));
}
}
首先我们把区间分成左右子树,如果查询的点落在左子树的rs里,那么我们可以分成左边查询x,和右边查询mid+1;同理,如果查询的点落在右子树的ls里,那么我们可以分成右边查询x,左边查询mid来实现我们对于查询点的查询,这样相当于是区间查询中的分段,只不过把一段分成了许多个点然后分别进行加和。最后的if条件是剪枝加速用的,因为分到点速度太慢会TLE,所以如果一整段都是连通或者整一段都不连通就可以直接返回,加快速度!
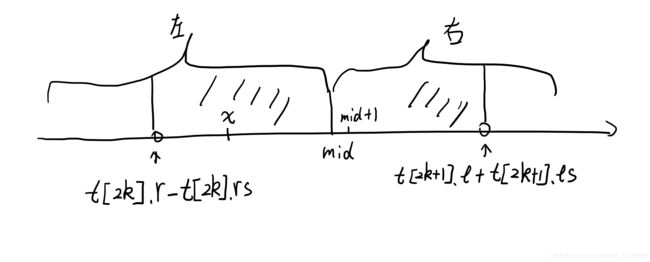
(原谅博主的渣画技)
4.代码:
//F - Tunnel Warfare
#includeM - Count Color(POJ 2777)
1.题目描述:
Chosen Problem Solving and Program design as an optional course, you are required to solve all kinds of problems. Here, we get a new problem.
There is a very long board with length L centimeter, L is a positive integer, so we can evenly divide the board into L segments, and they are labeled by 1, 2, … L from left to right, each is 1 centimeter long. Now we have to color the board - one segment with only one color. We can do following two operations on the board:
- “C A B C” Color the board from segment A to segment B with color C.
- “P A B” Output the number of different colors painted between segment A and segment B (including).
In our daily life, we have very few words to describe a color (red, green, blue, yellow…), so you may assume that the total number of different colors T is very small. To make it simple, we express the names of colors as color 1, color 2, … color T. At the beginning, the board was painted in color 1. Now the rest of problem is left to your.
Input
First line of input contains L (1 <= L <= 100000), T (1 <= T <= 30) and O (1 <= O <= 100000). Here O denotes the number of operations. Following O lines, each contains “C A B C” or “P A B” (here A, B, C are integers, and A may be larger than B) as an operation defined previously.
Output
Ouput results of the output operation in order, each line contains a number.
Sample Input
2 2 4
C 1 1 2
P 1 2
C 2 2 2
P 1 2
Sample Output
2
1
2.题意:
你有一个区间[1,n]要染色,默认为颜色为1,每次操作分为:区间染色,或者查询区间内不同的颜色数。
3.思路:
线段树+bitset。题目强调了染色的数目不多(T<=30),因此直接暴力开一个31的bitset,区间更新其实就是左子树与右子树的bitset或起来(同种颜色只算一次嘛),bitset可以更快,而且省空间。唯一可能要注意的点是查询,因为左右分区间的时候,左右两边的区间颜色数目可能有重叠,因此查询不能直接返回对应区间的颜色加和,而是把区间颜色相或,然后再计数。 【由于bitset对于这种存在与否问题的处理极佳,所以强烈建议去学一下bitset!】
4.代码:
//M - Count Color
#include//我会补完的QAQ