PyTorch 笔记(13)— autograd(0.4 之前和之后版本差异)、Tensor(张量)、Gradient(梯度)
1. 背景简述
torch.autograd 是 PyTorch 中方便用户使用,专门开发的一套自动求导引擎,它能够根据输入和前向传播过程自动构建计算图,并执行反向传播。
计算图是现代深度学习框架 PyTorch、TensorFlow 等的核心,它为自动求导算法——反向传播提供了理论支持。
PyTorch 的 Autograd 模块实现了深度学习的算法中的反向传播求导数,在张量(Tensor 类)上的所有操作,Autograd 都能为他们自动提供微分,简化了手动计算导数的复杂过程。
在 0.4 以前的版本中,Pytorch 使用 Variable 类来自动计算所有的梯度。
从 0.4 起, Variable 正式合并入 Tensor 类,通过 Variable 嵌套实现的自动微分功能已经整合进入了Tensor 类中。虽然为了代码的兼容性还是可以使用 Variable(tensor) 这种方式进行嵌套,但是这个操作其实什么都没做。
所以,以后的代码建议直接使用 Tensor 类进行操作,因为官方文档中已经将 Variable 设置成过期模块。
要想通过 Tensor 类本身就使用 autograd 功能,只需要设置 .requries_grad=True
Variable 类中的的 grad 和 grad_fn 属性已经整合进入了 Tensor 类中。
关于反向传播的基础,请参考:浅显易懂的计算图
2. autograd(PyTorch 0.4 之前版本)
PyTorch 在 autograd 模块中实现了计算图的相关功能,autograd 的核心数据结构是 Variable 。
Variable 封装了 tensor,并记录对 tensor 的操作记录用来构建计算图。
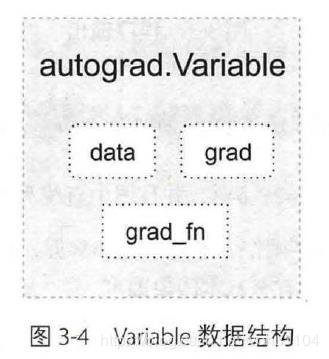
Variable 的数据结构如下图所示,主要包含三个属性:
data: 保存Variable所包含的tensor;grad:保存data对应的梯度,grad也是variable而非tensor,与data形状一致;grad_fn:指向一个Function,这个Function用来反向传播计算输入的梯度,记录variable的操作历史,即它是什么操作的输出,用来构建计算图。如果某一个变量是由用户创建的,则它为叶子节点,对应的grad_fn为None;
Variable 的构造函数需要传入 tensor,同时有两个可选参数:
requires_grad(bool):是否需要对该variable进行求导;volatile(bool): 意为“挥发”,设置为True,构建在该variable上的图都不会求导,专为推理阶段设计;
早期 Variable 的创建是需要 tensor,类似这样:
In [8]: a = V(t.ones(3,4), requires_grad=True)
目前 Pytorch 的版本已经可以直接这样:
In [11]: b = t.ones(3,4).requires_grad_(True)
不区分 tensor 和 Variable ,Tensors/Variables 合并,弃用 volatile 标志,原来若 True ,在这之后的图都不会求导。
Variable 支持大部分的 tensor 支持的函数,但不支持部分 inplace 函数。因为这些操作会修改 tensor 自身,而在反向传播中,variable 需要缓存原来的 tensor 来计算梯度。如果想要计算各个 Variable 的梯度,只需调用根节点 variable 的 backward 方法,autograd 会自动沿着计算图反向传播,计算每一个叶子节点的梯度。
variable.backward(grad_variables=None, retain_graph=None, create_graph=None)
主要有如下参数:
grad_variables:形状与variable一致,对于y.backward(),grad_variables相当于链式法则 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z = ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z ∂ y ∂ x \frac{\partial y}{\partial x} ∂x∂y 中的 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z,grad_variables也可以是tensor或序列。retain_graph:反向传播需要缓存一些中间结果,反向传播之后,这些缓存就被清空,可通过指定这个参数不清空缓存,用来多次反向传播。create_graph:对反向传播过程再次构建计算图,可通过backward of backward实现求高阶导数。
In [1]: import torch as t
In [2]: a = t.ones(3,4).requires_grad_(True)
In [3]: a
Out[3]:
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], requires_grad=True)
In [4]: b = t.zeros(3,4)
In [5]: b
Out[5]:
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
In [6]: c = a + b
In [7]: c
Out[7]:
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]], grad_fn=<AddBackward0>)
In [8]: d = c.sum()
In [9]: d
Out[9]: tensor(12., grad_fn=<SumBackward0>)
In [10]: d.backward()
In [11]: a.grad
Out[11]:
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
In [12]: a.requires_grad
Out[12]: True
In [13]: b.requires_grad
Out[13]: False
此处虽然没有指定 c 需要求导,但 c 依赖于 a,而 a 需要求导因此 c 的 requires_grad 属性会自动设为True
In [14]: c.requires_grad
Out[14]: True
In [15]: a.is_leaf
Out[15]: True
In [16]: b.is_leaf
Out[16]: True
c 不是叶子节点
In [17]: c.is_leaf
Out[17]: False
3. autograd(PyTorch 0.4 之后版本)
3.1 Tensor(张量)
torch.Tensor 是这个包的核心类。如果设置它的属性 .requires_grad 为 True,那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用 .backward(),来自动计算所有的梯度。这个张量的所有梯度将会自动累加到 .grad 属性。
要阻止一个张量被跟踪历史,可以调用.detach() 方法将其与计算历史分离,并阻止它未来的计算记录被跟踪。
在张量创建时,通过设置 requires_grad=True 来告诉 Pytorch 需要对该张量进行自动求导,PyTorch 会记录该张量的每一步操作历史并自动计算, 以下两种方法是等价的。
In [1]: import torch as t
In [2]: x = t.ones(2,2,requires_grad=True)
In [3]: a = t.ones(2,2).requires_grad_(True)
In [4]: a
Out[4]:
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
In [5]: x
Out[5]:
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
In [6]:
针对张量 x 做一次运算
In [6]: y = x + 2
In [7]: y
Out[7]:
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward0>)
In [8]:
y 是计算的结果,而不是用户自己创建的,所以它有 grad_fn 属性。
x 是用户自己创建的,所以 grad_fn 为 None。
在张量进行操作后,grad_fn 已经被赋予了一个新的函数,这个函数引用了一个创建了这个 Tensor 类的Function 对象。 Tensor 和 Function 互相连接生成了一个非循环图,它记录并且编码了完整的计算历史。每个张量都有一个 .grad_fn 属性,如果这个张量是用户手动创建的那么这个张量的 grad_fn 是 None 。
In [8]: y.grad_fn
Out[8]: <AddBackward0 at 0x4bdce50>
In [10]: x.grad_fn
In [11]:
对 y 进行更多操作,z=3x2+12x+12,
In [11]: z = y*y*3
In [12]: z
Out[12]:
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>)
In [13]: z.mean()
Out[13]: tensor(27., grad_fn=<MeanBackward0>)
In [14]:
.requires_grad_(...) 原地改变了现有张量的 requires_grad 标志。如果没有指定的话,默认输入的这个标志是 False。
In [15]: a = t.randn(2,2)
In [16]: a = ((a*3) /(a-1))
In [17]: a.requires_grad
Out[17]: False
In [18]: a.requires_grad_(True)
Out[18]:
tensor([[ 0.6064, -11.8267],
[ 0.5640, 9.0712]], requires_grad=True)
In [19]: a.requires_grad
Out[19]: True
In [20]: b = (a*a).sum()
In [21]: b.grad_fn
Out[21]: <SumBackward0 at 0x100f7490>
In [22]:
3.2 Gradient(梯度)
为了防止跟踪历史记录(和使用内存),可以将代码块包装在
with torch.no_grad():
中。在评估模型时特别有用,因为模型可能具有 requires_grad = True 的可训练的参数,但是我们不需要在此过程中对他们进行梯度计算。
还有一个类对于 autograd 的实现非常重要:Function 。
Tensor 和 Function 互相连接并构建一个非循环图,它保存整个完整的计算过程的历史信息。每个张量都有一个 .grad_fn 属性,该属性引用了创建 Tensor自身的 Function 。(除非这个张量是用户手动创建的,即这个张量的 grad_fn 是 None )。
如果需要计算导数,可以在 Tensor上调用 .backward()。
- 如果
Tensor是一个标量(即它包含一个元素的数据),则不需要为backward()指定任何参数; - 如果它有更多的元素,则需要指定一个
gradient参数,该参数是形状匹配的张量;
3.2.1 简单自动求导
PyTorch 会自动追踪和记录对与张量的所有操作,当计算完成后调用 .backward() 方法自动计算梯度并且将计算结果保存到 grad 属性中。
如果 Tensor 类表示的是一个标量(即它包含一个元素的张量),则不需要为 backward() 指定任何参数,如下所示 out 是一个标量,因此 out.backward() 和 out.backward(torch.tensor(1.)) 等价 。这种参数常出现在图像分类中的单标签分类,输出一个标量代表图像的标签。
因为 对 y 进行更多操作后 z=3x2+12x+12,所以 out=z/4,
In [22]: out = z.mean()
In [23]: out
Out[23]: tensor(27., grad_fn=<MeanBackward0>)
In [24]: out.backward()
输出导数 d(out)/dx=x.grad
In [25]: x.grad
Out[25]:
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
我们的得到的是一个数取值全部为 4.5 的矩阵。让我们来调用 out 张量 O。
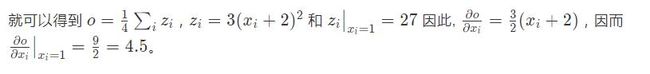
3.2.2 复杂自动求导
如果 Tensor 类包含多个参数,则需要指定一个 gradient 参数,它是形状匹配的张量。
我们来看看 autograd 计算的导数和我们手动推导的导数的区别。以下函数
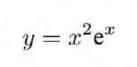
的导数为:
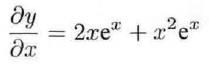
In [23]: def f(x):
...: y = x**2 * t.exp(x)
...: return y
...:
In [24]: def gradf(x):
...: dx = 2*x*t.exp(x) + x**2*t.exp(x)
...: return dx
...:
In [25]: x = t.randn(2,3).requires_grad()
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-25-95892a3a5546> in <module>
----> 1 x = t.randn(2,3).requires_grad()
TypeError: 'bool' object is not callable
In [26]: x = t.randn(2,3).requires_grad
In [27]: x
Out[27]: False
In [28]: x = t.randn(2,3).requires_grad_()
In [29]: x
Out[29]:
tensor([[-0.9131, -0.8917, 0.4434],
[-1.1244, -0.1586, 0.5543]], requires_grad=True)
In [30]: y = f(x)
In [31]: gradf(x)
Out[31]:
tensor([[-0.3982, -0.4051, 1.6880],
[-0.3198, -0.2492, 2.4649]], grad_fn=<AddBackward0>)
因为 y 不是一个标量,所以需要输入一个大小相同的张量作为参数,这里我们用 t.ones(y.size()) 函数根据 x 生成一个张量。
t.ones(y.size())
和
t.ones_like(y)
等价。
In [32]: y.backward
Out[32]:
<bound method Tensor.backward of tensor([[0.3346, 0.3260, 0.3063],
[0.4107, 0.0215, 0.5349]], grad_fn=<MulBackward0>)>
In [33]: y.backward(t.ones(y.size()))
In [34]: x.grad
Out[34]:
tensor([[-0.3982, -0.4051, 1.6880],
[-0.3198, -0.2492, 2.4649]])
In [35]:
可以看到自动求导和手动求导结果是相等的。
3.2.3 torch.no_grad()
我们可以使用 with torch.no_grad() 上下文管理器临时禁止对已设置 requires_grad=True 的张量进行自动求导。这个方法在测试集计算准确率的时候会经常用到,例如:
In [32]: x = t.ones(2,3, requires_grad=True)
In [33]: y = 2*x*x
In [34]: y.requires_grad
Out[34]: True
In [35]: with t.no_grad():
...: print(y.requires_grad)
...:
True
In [36]:
这块应该为 False,但不知道为啥实际测试是 True,带继续深入了解。
使用 .no_grad() 进行嵌套后,代码不会跟踪历史记录,也就是说保存的这部分记录会减少内存的使用量并且会加快少许的运算速度。
3.3 Autograd 过程
- 当我们执行
z.backward()的时候。这个操作将调用z里面的grad_fn这个属性,执行求导的操作。 - 这个操作将遍历
grad_fn的next_functions,然后分别取出里面的Function(AccumulateGrad),执行求导操作。这部分是一个递归的过程直到最后类型为叶子节点。 - 计算出结果以后,将结果保存到他们对应的
variable这个变量所引用的对象(x和y)的grad这个属性里面。 - 求导结束。所有的叶节点的
grad变量都得到了相应的更新
最终当我们执行完 z.backward() 之后,x 和 y 里面的 grad 值就得到了更新。
3. 扩展 Autograd
如果需要自定义 autograd 扩展新的功能,就需要扩展 Function 类。因为 Function 使用 autograd 来计算结果和梯度,并对操作历史进行编码。 在 Function类 中最主要的方法就是 forward() 和 backward() 它们分别代表了前向传播和反向传播。
一个自定义的 Function 需要一下三个方法:
-
__init__ (optional):如果这个操作需要额外的参数则需要定义这个Function的构造函数,不需要的话可以忽略。 -
forward():执行前向传播的计算代码 -
backward():反向传播时梯度计算的代码。 参数的个数和forward返回值的个数一样,每个参数代表传回到此操作的梯度。
In [37]:
...: # 引入Function便于扩展
...: from torch.autograd.function import Function
In [38]: # 定义一个乘以常数的操作(输入参数是张量)
...: # 方法必须是静态方法,所以要加上@staticmethod
...: class MulConstant(Function):
...: @staticmethod
...: def forward(ctx, tensor, constant):
...: # ctx 用来保存信息这里类似self,并且ctx的属性可以在backward中调用
...: ctx.constant=constant
...: return tensor *constant
...: @staticmethod
...: def backward(ctx, grad_output):
...: # 返回的参数要与输入的参数一样.
...: # 第一个输入为3x3的张量,第二个为一个常数
...: # 常数的梯度必须是 None.
...: return grad_output, None
...:
In [39]:
定义完我们的新操作后,我们来进行测试
In [40]: a=t.rand(3,3,requires_grad=True)
In [41]: a
Out[41]:
tensor([[0.2859, 0.6373, 0.3489],
[0.7932, 0.1416, 0.0118],
[0.2317, 0.8374, 0.2620]], requires_grad=True)
In [42]: b=MulConstant.apply(a,5)
In [43]: b
Out[43]:
tensor([[1.4294, 3.1866, 1.7447],
[3.9661, 0.7079, 0.0591],
[1.1584, 4.1870, 1.3099]], grad_fn=<MulConstantBackward>)
In [44]:
反向传播,返回值不是标量,所以 backward 方法需要参数。
In [45]: b.backward(t.ones_like(a))
In [46]: a.grad
Out[46]:
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
In [47]:
参考:
- https://github.com/zergtant/pytorch-handbook/blob/master/chapter2/2.1.2-pytorch-basics-autograd.ipynb
- https://pytorch.apachecn.org/docs/1.4/blitz/autograd_tutorial.html