PyTorch 笔记（14）— nn.module 实现简单感知机和多层感知机

autograd 实现了自动微分系统，然而对深度学习来说过于底层，而本节将介绍 nn 模块，是构建于 autograd 之上的神经网络模块。

1. 简单感知机

使用 autograd 可实现深度学习模型，但其抽象程度较低，如果用其来实现深度学习模型，则需要编写的代码量极大。在这种情况下，torch.nn 应运而生，其是专门为深度学习设计的模块。

torch.nn 的核心数据结构是 Module ，它是一个抽象的概念，既可以表示神经网络中的某个层（layer），也可以表示一个包含很多层的神经网络。

在实际使用中，最常见的做法继承 nn.Module ，撰写自己的网络层。

下面先来看看如何使用 nn.Module 实现自己的全连接层。全连接层，又名仿射层，输入 y 和输入 x 满足y=xW+b ，W 和 b 是可学习的参数。

import torch as t
from torch import  nn

class Linear(nn.Module):
    def __init__(self, input_features, out_features):
        super(Linear, self).__init__() # 等价于 nn.Module.__init__(self)
        
        self.w = nn.Parameter(t.randn(input_features, out_features))
        self.b = nn.Parameter(t.randn(out_features))
    
    def forward(self, x):
        x = x.mm(self.w)
        return x + self.b.expand_as(x)
    
layer = Linear(4, 3)

x = t.randn(2, 4)
output = layer(x)
print output

for name, parameter in layer.named_parameters():
    print name, parameter

output 输出为 ：

tensor([[ 1.5752,  0.6730, -0.0763],
        [-0.7037, -0.6641, -2.3261]], grad_fn=<ThAddBackward>)

name, parameter 输出为：

w Parameter containing:
tensor([[-1.0459, -0.1899,  0.2202],
        [ 1.5751,  0.0613,  1.7350],
        [-0.2644,  0.7728,  1.4141],
        [-0.3739, -0.4349, -0.0984]], requires_grad=True)
b Parameter containing:
tensor([1.3054, 0.3063, 0.4375], requires_grad=True)

可见，全连接层的实现非常简单，但需注意以下几点：

• 自定义层 Linear 必须继承 nn.Module ，并且在其构造函数中需调用 nn.Module 的构造函数，即super(Linear,self).__init()__ 或 nn.Module.__init(self)__；
• 在构造函数 __init__ 中必须自己定义可学习的参数，并封装成 Parameter，如在本例中我们把 w 和 b 封装成 Parameter 。Parameter 是一种特殊的 Variable ，但其默认需要求导（requires_grad=True ）；
• forward 函数实现前向传播过程，其输入可以是一个或多个 variable，对 x 的任何操作也必须是 variable 支持的操作。
• 无须写反向传播函数，因其前向传播都是对 variable 进行操作，nn.Module 能够利用 autograd 自动实现反向传播，这一点比 Function 简单许多。
• 使用时，直观上可将 layer 看成数学概念中的函数，调用 layer(input) 即可得到 input 对应的结果。它等价于 layers.__call(input)__ ，在 __call__ 函数中，主要调用的是 layer.forward(x) 。所以在实际使用中应尽量使用layer(x) 而不是使用 layer.forward(x) 。
• Module 中的可学习参数可以通过 named_parameters() 或者 parameters() 返回迭代器，前者会给每个parameter 附上名字，使其更具有辨识度。

可见，利用 Module 实现的全连接层，比利用 Function 实现的更简单，因其不再需要写反向传播函数。

2. 多层感知机

Module 能够自动检测到自己的 parameter ，并将其作为学习参数。除了 parameter，Module 还包含子Module ，主 Module 能够递归查找子 Module 中的 parameter 。下面再来看看稍微复杂一点的网络：多层感知机。

多层感知机的网络结构如图所示。它由两个全连接层组成，采用 sigmoid 函数作为激活函数（图中没有画出）。

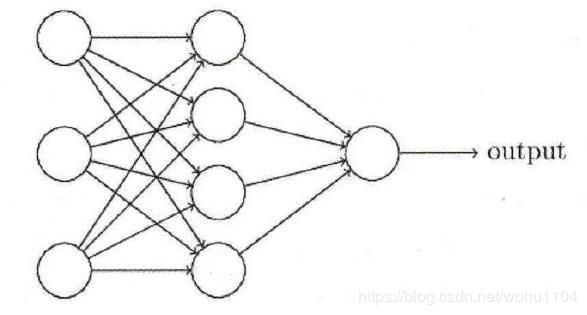
实现代码如下：

import torch as t
from torch import  nn

class Linear(nn.Module):
    def __init__(self, input_features, out_features):
        super(Linear, self).__init__() # 等价于 nn.Module.__init__(self)
        
        self.w = nn.Parameter(t.randn(input_features, out_features))
        self.b = nn.Parameter(t.randn(out_features))
    
    def forward(self, x):
        x = x.mm(self.w)
        return x + self.b.expand_as(x)

class Perceptron(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        nn.Module.__init__(self)
        self.layer1 = Linear(in_features, hidden_features) # 此处的 Linear 前面自定义的全连接层
        self.layer2 = Linear(hidden_features, out_features)
    
    def forward(self, x):
        x = self.layer1(x)
        x = t.sigmoid(x)
        return self.layer2(x)

perception = Perceptron(3,4,1)
for name, param in perception.named_parameters():
    print(name, param.size())

输出结果：

layer1.w torch.Size([3, 4])
layer1.b torch.Size([4])
layer2.w torch.Size([4, 1])
layer2.b torch.Size([1])

可见，即使是稍复杂的多层感知机，其实现依旧很简单。这里需要注意以下两个知识点。

• 构造函数 __init__ 中，可利用前面自定义的 Linear 层（ Module ）作为当前 Module 对象的一个子Module ，它的可学习参数，也会成为当前 Module 的可学习参数。

• 在前向传播函数中，我们有意识地将输出变量都命名为 x，是为了能让 Python 回收一些中间层的输出，从而节省内存。但并不是所有的中间结果都会被回收，有些 variable 虽然名字被覆盖，但其在反向传播时仍需要用到，此时 Python 的内存回收模块将通过检查引用计数，不会回收这一部分内存。

Module 中 parameter 的全局命名规范如下：

• Parameter 直接命名。例如 self.param_name = nn.Parameter(t.randn(3,4)) ，命名为 param_name 。
• 子 Module 中的 parameter ，会在其名字之前加上当前 Module 的名字。例如 self.sub_module = SubModule() ， SubModule 中有个 parameter 的名字也叫作 param_name ，那么二者拼接而成的 parameter name 就是sub_module.param_name 。

为了方便用户使用，PyTorch 实现了神经网络中绝大多数的 layer ，这些 layer 都继承于 nn.Module ，封装了可学习参数 parameter ，并实现了 forward 函数，且专门针对 GPU 运算进行了 CuDNN 优化，其速度和性能都十分优异。

• 构造函数的参数，如 nn.Linear(in_features,out_features,bias)，需关注这三个参数的作用。
• 属性、可学习参数和子 Module 。如 nn.Linear 中有 weight 和 bias 两个可学习参数，不包含子 Module 。
• 输入输出的形状，如 nn.Linear 的输入形状是（N，input_features），输出形状为（N，output_features），N 是 batch_size 。

这些自定义 layer 对输入形状都有假设：输入的不是单个数据，而是一个 batch 。若想输入一个数据，必须调用 unsqueeze(0) 函数将数据伪装成 batch_size=1 的 batch 。