算法笔记之排序
最近在看《算法笔记》,如果单从算法来说,这本书真正做到了短小精悍,首先以排序入题,那么我们今天也来说说排序。
排序
将一堆杂乱无章的元素按照某种规则有序排列的过程就叫“排序”.排序是一种非常基础的算法,有着广泛的理论和实践基础。对一个排序算法来说,一般从如下3个方面衡量算法的优劣:
- 时间复杂度:主要是分析关键字的比较次数和记录的移动次数。
- 空间复杂度:分析排序算法中需要多少辅助内存
- 稳定性:若两个记录A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种算法是稳定的;反之,就是不稳定的。
排序算法很多,我们按是否可以实现排序分为比较排序和非比较排序,在比较排序中常见的有,比较排序,梳排序,堆排序,归并排序,快递排序,内省排序等,非比较排序如,通排序,基数排序等。如果按传统的分类,则可以分为插入排序、折半插入排序、Shell排序、归并排序、直接选择排序、堆排序、冒泡排序、快速排序、桶式排序、基数排序等,各大排序基于不同的场景设置,各有优势。接下来就选取几个常见的说明。
比较排序
在常见的排序算法中,大多数排序都属于这一种。在比较排序中,排序对象可以是任何类型,我们只需要知道如何比较两个对象的大小。
定义1(基于比较的排序)
给定一个包含n个对象的待排序对象a1,a2...an。假设我们知道如何比较其中任意两个对象的大小,那么我们就可以对这列数据进行排序。
基于比较排序必须知道两个对象的大小。对于比较排序应满足以下两个性质:传递性和全序性。
传递性:如果a≤b,b≤c,则一定有a≤c。
全序性:对任意的a和b,或者a≤b,或者b≤a。
定义2,(合并多个有序列)
将n个有序列合并为一个有序列,这n个有序列的长度分别为m1,m2...mn。
合并多个有序列的应用场景。例如我们要检索一个数据库,而检索结果只需要满足多个条件的某一个。这时我们可以先进行单一检索,然后将这些检索结果进行合并。而单一检索往往是可以通过快速检索完成的。
定义3,(前k序列的小数)
给定一个n个对象的序列,找出前k个最新的数。例如,当检索结果太多的时候,我们可以根据某个评价标准列出值得展示的k个结果作为参考,这样避免全部排序。
梳排序
梳排序和希尔排序很类似。希尔排序是在直接插入排序的基础上做的优化,而梳排序是在冒泡排序的基础上做的优化。也是想希尔排序一样,将待排序序列通过增量分为若干个子序列,然后对子序列进行一趟冒泡排序,一步步减小增量,直至增量为1。所以梳排序的最后一次排序是冒泡排序。
梳排序增量是根据递减率减小的,递减率的设定影响着梳排序的效率,原作者以随机数作实验,得到最有效递减率为1.3的。
举个例子:待排序序列为{8, 6, 5, 2, 1, 4, 3,7}
(1)初始increment = 8/1.3 =6。分为子序列{8, 3}{6, 7}{5}{2}{1}{4}进行一趟冒泡排序,得到{3, 6, 5, 2, 1, 4, 8, 7}
(2)increment = 6/1.3 = 4。分为子序列{3, 1}{6, 4}{5, 8}{2, 7}进行一趟冒泡排序,得到{1, 4, 5, 2, 3, 6, 8, 7}。
(3)increment = 4/1.3 = 3。分为子序列{1, 2, 8}{4, 3, 7}{5, 6}进行一趟冒泡排序,得到{1, 3, 5, 2, 4, 6, 8, 7}。
(4)increment = 3/1.3 = 2。分为子序列{1, 5, 4, 8}{3, 2, 6, 7}进行一趟冒泡排序,得到{1, 2, 4, 3, 5, 6, 8, 7}。
(5)increment = 2/1.3 = 1。分为子序列{1, 2, 4, 3, 5, 6, 8, 7}进行一趟冒泡排序,得到{1, 2, 3, 4, 5, 6, 7, 8}。
(2)increment = 6/1.3 = 4。分为子序列{3, 1}{6, 4}{5, 8}{2, 7}进行一趟冒泡排序,得到{1, 4, 5, 2, 3, 6, 8, 7}。
(3)increment = 4/1.3 = 3。分为子序列{1, 2, 8}{4, 3, 7}{5, 6}进行一趟冒泡排序,得到{1, 3, 5, 2, 4, 6, 8, 7}。
(4)increment = 3/1.3 = 2。分为子序列{1, 5, 4, 8}{3, 2, 6, 7}进行一趟冒泡排序,得到{1, 2, 4, 3, 5, 6, 8, 7}。
(5)increment = 2/1.3 = 1。分为子序列{1, 2, 4, 3, 5, 6, 8, 7}进行一趟冒泡排序,得到{1, 2, 3, 4, 5, 6, 7, 8}。
代码实现:(这里貌似是C,后面再改吧)
BOOL CombSort(datatype *array, int size)
{
int i, j;
int increment;
if(array == NULL ) {
return FALSE;
}
increment = size;
while(TRUE) {
increment = (int)(increment / LAPSE_RATE);
for(i = 0; i < increment; i++) {
for(j = i+increment; j < size; j += increment) {
if(array[j] < array[j-increment]) {
Swap(array+j, array+j-increment);
}
}
}
if(increment <= 1) {
break;
}
}
return TRUE;
}堆排序
堆是一种重要的数据结构,为一棵完全二叉树, 底层如果用数组存储数据的话,假设某个元素为序号为i(Java数组从0开始,i为0到n-1),如果它有左子树,那么左子树的位置是2i+1,如果有右子树,右子树的位置是2i+2,如果有父节点,父节点的位置是(n-1)/2取整。分为最大堆和最小堆,最大堆的任意子树根节点不小于任意子结点,最小堆的根节点不大于任意子结点。所谓堆排序就是利用堆这种数据结构来对数组排序,我们使用的是最大堆。处理的思想和冒泡排序,选择排序非常的类似,一层层封顶,只是最大元素的选取使用了最大堆。最大堆的最大元素一定在第0位置,构建好堆之后,交换0位置元素与顶即可。堆排序为原位排序(空间小), 且最坏运行时间是O(nlgn),是渐进最优的比较排序算法。
堆排序的大概步骤如下:
- 构建最大堆。
- 选择顶,并与第0位置元素交换
- 由于步骤2的的交换可能破环了最大堆的性质,第0不再是最大元素,需要调用maxHeap调整堆(沉降法),如果需要重复步骤2
做堆排序需要实现一个工具类,
代码实现(ArrayUtils )
public class ArrayUtils {
public static void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
public static void exchangeElements(int[] array, int index1, int index2) {
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
}demo
public class HeapSort {
public static void main(String[] args) {
int[] array = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3 };
System.out.println("Before heap:");
ArrayUtils.printArray(array);
heapSort(array);
System.out.println("After heap sort:");
ArrayUtils.printArray(array);
}
public static void heapSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
buildMaxHeap(array);
for (int i = array.length - 1; i >= 1; i--) {
ArrayUtils.exchangeElements(array, 0, i);
maxHeap(array, i, 0);
}
}
private static void buildMaxHeap(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int half = array.length / 2;
for (int i = half; i >= 0; i--) {
maxHeap(array, array.length, i);
}
}
private static void maxHeap(int[] array, int heapSize, int index) {
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
if (left < heapSize && array[left] > array[index]) {
largest = left;
}
if (right < heapSize && array[right] > array[largest]) {
largest = right;
}
if (index != largest) {
ArrayUtils.exchangeElements(array, index, largest);
maxHeap(array, heapSize, largest);
}
}
} 归并排序
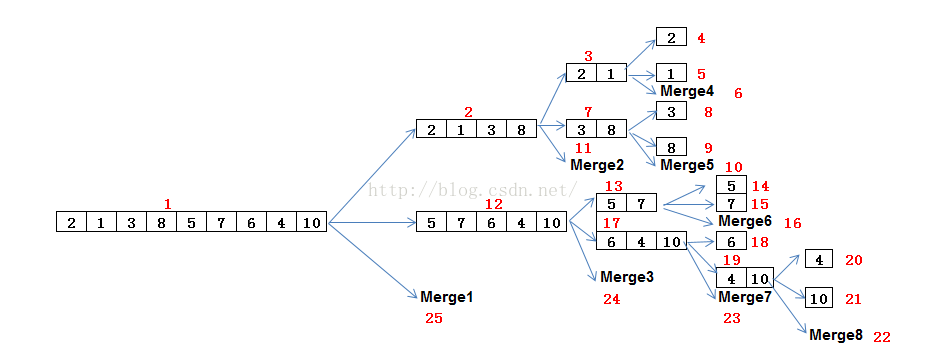
归并排序是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
归并排序算法稳定,数组需要O(n)的额外空间,链表需要O(log(n))的额外空间,时间复杂度为O(nlog(n)),算法不是自适应的,不需要对数据的随机读取。
归并排序的使用步骤:
1、申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
2、设定两个指针,最初位置分别为两个已经排序序列的起始位置
3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
4、重复步骤3直到某一指针达到序列尾
5、将另一序列剩下的所有元素直接复制到合并序列尾
2、设定两个指针,最初位置分别为两个已经排序序列的起始位置
3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
4、重复步骤3直到某一指针达到序列尾
5、将另一序列剩下的所有元素直接复制到合并序列尾
代码实现
public class MergeSortTest {
public static void main(String[] args) {
int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
print(data);
mergeSort(data);
System.out.println("排序后的数组:");
print(data);
}
public static void mergeSort(int[] data) {
sort(data, 0, data.length - 1);
}
public static void sort(int[] data, int left, int right) {
if (left >= right)
return;
// 找出中间索引
int center = (left + right) / 2;
// 对左边数组进行递归
sort(data, left, center);
// 对右边数组进行递归
sort(data, center + 1, right);
// 合并
merge(data, left, center, right);
print(data);
}
/**
* 将两个数组进行归并,归并前面2个数组已有序,归并后依然有序
*
* @param data
* 数组对象
* @param left
* 左数组的第一个元素的索引
* @param center
* 左数组的最后一个元素的索引,center+1是右数组第一个元素的索引
* @param right
* 右数组最后一个元素的索引
*/
public static void merge(int[] data, int left, int center, int right) {
// 临时数组
int[] tmpArr = new int[data.length];
// 右数组第一个元素索引
int mid = center + 1;
// third 记录临时数组的索引
int third = left;
// 缓存左数组第一个元素的索引
int tmp = left;
while (left <= center && mid <= right) {
// 从两个数组中取出最小的放入临时数组
if (data[left] <= data[mid]) {
tmpArr[third++] = data[left++];
} else {
tmpArr[third++] = data[mid++];
}
}
// 剩余部分依次放入临时数组(实际上两个while只会执行其中一个)
while (mid <= right) {
tmpArr[third++] = data[mid++];
}
while (left <= center) {
tmpArr[third++] = data[left++];
}
// 将临时数组中的内容拷贝回原数组中
// (原left-right范围的内容被复制回原数组)
while (tmp <= right) {
data[tmp] = tmpArr[tmp++];
}
}
public static void print(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + "\t");
}
System.out.println();
}
} 快速排序
快速排序也是我们常用的排序,快速排序和归并排序都使用分治法来设计算法,区别在于归并排序把数组分为两个基本等长的子数组,分别排好序之后还要进行归并(Merge)操作,而快速排序会取一个基准元素,拆分之后基准元素左边的元素都比基准元素小,右边的元素都不小于基准元素,这样只需要分别对两个子数组排序即可,不再像归并排序一样需要归并操作。
快速排序最坏运行时间:当输入数组已排序时,时间为O(n^2),最佳为O(nlgn)。
快速排序同样需要先实现一个工具类。
public class ArrayUtils {
public static void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
public static void exchangeElements(int[] array, int index1, int index2) {
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
} public class QuickSort {
public static void main(String[] args) {
int[] array = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3 };
System.out.println("Before sort:");
ArrayUtils.printArray(array);
quickSort(array);
System.out.println("After sort:");
ArrayUtils.printArray(array);
}
public static void quickSort(int[] array) {
subQuickSort(array, 0, array.length - 1);
}
private static void subQuickSort(int[] array, int start, int end) {
if (array == null || (end - start + 1) < 2) {
return;
}
int part = partition(array, start, end);
if (part == start) {
subQuickSort(array, part + 1, end);
} else if (part == end) {
subQuickSort(array, start, part - 1);
} else {
subQuickSort(array, start, part - 1);
subQuickSort(array, part + 1, end);
}
}
private static int partition(int[] array, int start, int end) {
int value = array[end];
int index = start - 1;
for (int i = start; i < end; i++) {
if (array[i] < value) {
index++;
if (index != i) {
ArrayUtils.exchangeElements(array, index, i);
}
}
}
if ((index + 1) != end) {
ArrayUtils.exchangeElements(array, index + 1, end);
}
return index + 1;
}
} 插入排序
插入排序就是把当前待排序的元素插入到一个已经排好序的列表里面。插入排序的最坏运行时间是O(n2), 所以并不是最优的排序算法。
插入排序比较常见我们这里就不在重点讲解。
public class InsertSortTest {
public static void insertSort(int[] array) {
if (array == null || array.length < 2) {
return;
}
for (int i = 1; i < array.length; i++) {
int currentValue = array[i];
int position = i;
for (int j = i - 1; j >= 0; j--) {
if (array[j] > currentValue) {
array[j + 1] = array[j];
position -= 1;
} else {
break;
}
}
array[position] = currentValue;
}
}
public static void main(String[] args) {
int[] array = { 3, -1, 0, -8, 2, 1 };
ArrayUtils.printArray(array);
insertSort(array);
ArrayUtils.printArray(array);
}
} 内省排序
内省排序又称Introsort,是一个相当偏门的排序算法,是由David Musser在1997年设计出来的。属于比较排序算法的一种。内省排序的实现过程是这样的,首先由快速排序开始,当递归深度超过一定程度时,转换为堆排序。所以内省排序既能在常规数据集上实现快速排序的高性能,又能在最坏情况下仍保持 O(N log N) 的时间复杂度。
内省排序就是快速排序,插入排序和堆排序混合而成的排序算法。
基于这种原理,摘自网上的内省升序和内省降序。
/**
* 内省排序升序
*/
public static int sort_neixing_asc(int[] array, int start, int end,
int level) {
// 先进行快速排序,当递归深度到达一定深度时,进行堆排序
// 改动快速排序代码,增加返回值为递归次数,当次数大于一定值时停止递归,开始调用堆排序进行排序
level++;
int length = end - start + 1;
if (length < 2)
return level;
else if (length == 2) {
if (array[start] > array[end]) {
int temp = array[end];
array[end] = array[start];
array[start] = temp;
}
return level;
} else {
// 得出最大值和最小值
int min = array[start], max = array[start];
for (int i = start; i < start + length; i++) {
if (array[i] < min)
min = array[i];
if (array[i] > max)
max = array[i];
}
// 找出合适的中间数(按中间值找,最好是像计数排序一样先统计比元素小的个数,然后按照个数确定哪个做中间数)
int absMid = (min + max) / 2;
int offset = Math.abs(array[start] - absMid);
int relativeMid = array[start];
int midIndex = start;
for (int i = start; i < start + length; i++)
if (Math.abs(array[i] - absMid) < offset) {
offset = Math.abs(array[i] - absMid);
relativeMid = array[i];
}
int[] newArray = new int[length];
for (int i = 0; i < newArray.length; i++)
newArray[i] = -1;
for (int i = start, startIndex = 0, endIndex = length - 1; i < start
+ length; i++) {
if (array[i] < relativeMid) {
newArray[startIndex] = array[i];
startIndex++;
} else if (array[i] > relativeMid) {
newArray[endIndex] = array[i];
endIndex--;
}
}
for (int i = 0; i < newArray.length; i++)
if (newArray[i] == -1)
newArray[i] = relativeMid;
for (int i = start, newIndex = 0; i < start + length; i++, newIndex++) {
array[i] = newArray[newIndex];
if (array[i] == relativeMid)
midIndex = i;
}
if (level < 10) {// 递归深度小于10时使用快速排序
sort_neixing_asc(array, start, midIndex - 1, level);
sort_neixing_asc(array, midIndex + 1, length - 1 + start, level);
} else {
// 递归深度大于10时使用堆排序
sort_dui_asc(array);
}
return level;
}
} /**
* 内省排序降序
*/
public static int sort_neixing_dasc(int[] array, int start, int end,
int level) {
// 先进行快速排序,当递归深度到达一定深度时,进行堆排序
// 改动快速排序代码,增加返回值为递归次数,当次数大于一定值时停止递归,开始调用堆排序进行排序
level++;
int length = end - start + 1;
if (length < 2)
return level;
else if (length == 2) {
if (array[start] < array[end]) {
int temp = array[end];
array[end] = array[start];
array[start] = temp;
}
return level;
} else {
// 得出最大值和最小值
int min = array[start], max = array[start];
for (int i = start; i < start + length; i++) {
if (array[i] < min)
min = array[i];
if (array[i] > max)
max = array[i];
}
// 找出合适的中间数(按中间值找,最好是像计数排序一样先统计比元素小的个数,然后按照个数确定哪个做中间数)
int absMid = (min + max) / 2;
int offset = Math.abs(array[start] - absMid);
int relativeMid = array[start];
int midIndex = start;
for (int i = start; i < start + length; i++)
if (Math.abs(array[i] - absMid) < offset) {
offset = Math.abs(array[i] - absMid);
relativeMid = array[i];
}
int[] newArray = new int[length];
for (int i = 0; i < newArray.length; i++)
newArray[i] = -1;
for (int i = start, startIndex = 0, endIndex = length - 1; i < start
+ length; i++) {
if (array[i] > relativeMid) {
newArray[startIndex] = array[i];
startIndex++;
} else if (array[i] < relativeMid) {
newArray[endIndex] = array[i];
endIndex--;
}
}
for (int i = 0; i < newArray.length; i++)
if (newArray[i] == -1)
newArray[i] = relativeMid;
for (int i = start, newIndex = 0; i < start + length; i++, newIndex++) {
array[i] = newArray[newIndex];
if (array[i] == relativeMid)
midIndex = i;
}
if (level < 10) {// 递归深度小于10时使用快速排序
sort_neixing_dasc(array, start, midIndex - 1, level);
sort_neixing_dasc(array, midIndex + 1, length - 1 + start,
level);
} else {
// 递归深度大于10时使用堆排序
sort_dui_dasc(array);
}
return level;
}
} 非比较排序
前面讲到了比较排序,他们普遍无法达到低于O(N log N)的时间复杂度。因此我们在使用排序算法的时候,通常会使用一些具有线性时间复杂度的算法。桶排序
桶排序可以认为是计数排序的推广。
桶排序:桶排序的思想是把区间[0,1)划分成n个相同大小的子区间,称为桶,然后将n个输入数分布到各个桶中去。 因为输入数均匀且独立分布在[0,1)上,所以,一般不会有很多数落在一个桶中的情况。 为了得到结果,先对各个桶中的数进行排序,然后按次序把各桶中的元素列出来。 桶排序的时间复杂度为O(n) 。
代码实现
public class BucketSort {
/**
* 桶排序算法,对arr进行桶排序,排序结果仍放在arr中
* @param arr
*/
static void bucketSort(double arr[]){
int n = arr.length;
ArrayList arrList[] = new ArrayList [n];
//把arr中的数均匀的的分布到[0,1)上,每个桶是一个list,存放落在此桶上的元素
for(int i =0;i1){
for(int i =1;i=0&&((Double)list.get(j)>(Double)list.get(j+1));j--)
list.set(j+1, list.get(j));
list.set(j+1, temp);
}
}
}
}
/**
* 测试.....
* 这里的测试数据是一个含n个元素的数组,且每个元素满足0<=arr[i]<1
*/
public static void main(String[] args) {
double arr[] = {0.78,0.17,0.39,0.26,0.72,0.94,0.21,0.12,0.23,0.68};
bucketSort(arr);
for(int i = 0;i 以上代码来源于网络,如有雷同,纯属偶然,谢谢。